Evaluación de tres algoritmos de segmentación del intervalo RT

Wong, Sara; Cruz, Julio; Gauvrit, Hervé; Hernández, Alfredo; La Cruz, Alexandra

La Dra. Sara Wong es Profesora en el Dpto. de Electrónica y Circuitos, Grupo de Bioingeniería y Biofísica Aplicada, Universidad Simón Bolívar, Apartado 89000, Caracas  1080-A, Venezuela, teléfono 58-212-906-4014, fax 58 212 9063631, correo electrónico swong@usb.ve .

El Dr. Julio Cruz es Profesor en el mismo departamento, teléfono y fax; correo electrónico jcsistemas2001@gmail.com .

El Dr. Revé Gauvrit es Maître de Conférences en el IUT de Rennes, Francia, Université de Reines, teléfono
33 223 236594, fax 33 2 2323 6917, correo electrónico herve.gauvrit@univ-rennes1.fr .

El Dr. Alfredo Hernández es Investigador INSERM, Francia, en la misma
Universidad, teléfono y fax, correo electrónico alfredo.hernandez@univ-rennes1.fr .

La Dra. Alexandra La Cruz es Profesora en el Dpto. de Computación y Tecnología de la Información, Grupo de Bioingeniería y Biofísica Aplicada, Universidad Simón Bolívar, Apartado 89000, Caracas 1080-a, Venezuela, teléfono 58 212 906-4014, fax 58 212 9063631, correo electrónico alacruz@ldc.usb.ve .
 

Resumen: En este trabajo se evalúan tres algoritmos de segmentación automática del intervalo RT. Estos algoritmos son: el algoritmo basado en un filtro derivador, el algoritmo basado en la descomposición de ondículas y el algoritmo basado en la modelización de la onda T. La evaluación se efectuó sobre señales electrocardiográficas sintéticas y reales. En la primera evaluación se contaminó un electrocardiograma (ECG) sintético con cuatro tipos de ruido en cuadro condiciones de Relación Señal a Ruido (SNR) (10, 15, 20 y 25 dB), en la segunda evaluación se compararon los resultados arrojados por los algoritmos con las anotaciones de dos expertos. Los resultados obtenidos muestran comportamientos satisfactorios de los tres enfoques en condiciones favorables de SNR. Sin embargo se observó un aumento de la variabilidad del intervalo RT inducida por el ruido.

Palabras clave: Algoritmos de segmentación/ ECG/ Intervalo RT/ Onda T/ Procesamiento de señales.

EVALUATION OF THREE SEGMENTATION ALGORITHMS IN THE RT INTERVAL

Abstract: Three automatics methods for the extraction of RT intervals are compared: the algorithm based on a derivate filter, the algorithm based on wavelets decomposition and the algorithm based on T wave modelization. The evaluation was carried on computer-generated and on real ECG signals. In the first evaluation, a synthetic electrocardiogram was contaminated with four types of noise in four conditions of Signal to Noise Ratio (SNR) (10, 15, 20 and 25 dB), in the second evaluation the algorithm’s results were compared with the annotations of two experts. The achieved performance shows a satisfying behavior of these approaches in favorable conditions of SNR. Nevertheless an increase of RT beat-to-beat variability induced by the artifacts was observed. 

Keywords: ECG/ RT Interval/ Segmentation/ Algorithms/ Signal Processing/ T Wave.

Manuscrito finalizado en Caracas el 2007/08/02, recibido el 2007/11/07, en su forma final (aceptado) el 2008/01/20.   

I. INTRODUCCIÓN 

Actualmente existe un gran interés en el estudio de la repolarización ventricular, pues un intervalo QT patológicamente largo es un hallazgo precoz de eventuales problemas de ritmo. En la Conferencia Europea de la Sociedad de Cardiología y de la Food and Drug Administration (FDA) [1] [2] se recomienda realizar la medida del intervalo QT durante la evaluación de nuevos medicamentos. Más aún, estas organizaciones instan a medir de forma semiautomática este intervalo con la ayuda del computador, para que el médico especialista pueda indicar al final de la onda T de cada latido o sobre un latido patrón con la ayuda del cursor. Las medidas clínicas del intervalo QT se realizan manualmente, promediando de tres a cinco mediciones realizadas sobre
latidos consecutivos.

Segmentar la duración de la repolarización ventricular consiste en detectar el máximo (Tmax) y el fin de la onda T (Tfin). Esta es una tarea delicada pues la onda T es de baja energía, vulnerable a diferentes tipos de ruidos y fuente de múltiples definiciones.

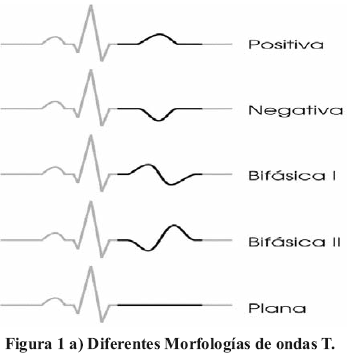
La definición de las ondas T bifásicas es relativamente compleja. El código de Minesota [3] define como onda T bifásica una onda T compuesta de dos puntos de inflexión con respecto a la línea isoeléctrica. El punto de inflexión designa el paso de una dirección horizontal o descendente a una dirección ascendente o un cambio inverso. Siguiendo la parte inicial de la onda T bifásica es negativa o negativa se habla de onda T bifásica + - u onda T bifásica -+ (Figura 1a). El uso de varias derivaciones es el mejor medio de determinar exactamente el final de la onda T. En ausencia de varias derivaciones, los expertos recomiendan utilizar el valor más largo encontrado en las derivaciones estándares, comúnmente en D2; sin embargo otros recomiendan la medición del
intervalo QT sobre las derivaciones precordiales V2 ó V3 donde el final de la onda T es fácilmente identificable. La medida manual del intervalo QT tampoco es simple; se distinguen dos métodos manuales, ilustrados en la Figura 1b, el método de la tangente, donde el final de la onda T está definido por el cruce por cero de esta línea (Tf1) y el método de la línea de base, en el cual el final de la onda T está definido por el cruce de la onda T por el nivel (isoeléctrico Tf2).

 

 

 

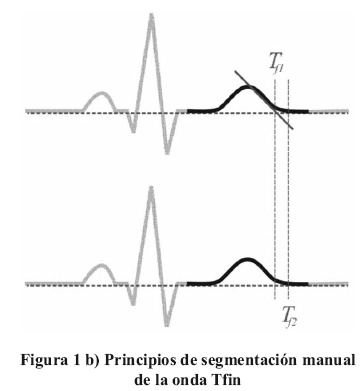
En este trabajo se evalúan tres algoritmos de segmentación automáticos utilizados ampliamente en la literatura. Estos algoritmos son: el algoritmo clásico de segmentación basado en un filtro derivador, el algoritmo basado en análisis multiresolución de ondículas y una propuesta basada en la modelización de la onda T. Los algoritmos fueron utilizados para medir intervalos RTmax y RTfin en lugar del intervalo QTmax o QTfin ya que la medida de la onda Q representa dificultades adicionales y no aportan informaciones suplementarias en el plan fisiológico [4].

II. DESARROLLO

1. Métodos

1.1. Algoritmo de la derivada filtrada (D1)

El primer detector (D1) se apoya en el postulado de que la cima de la onda T corresponde al cruce por cero de la derivada del electrocardiograma (ECG) [5]. La definición del final de la onda Tfin se basa en un criterio ad hoc. El algoritmo se descompone en varias etapas, primero se realiza un preprocesamiento del ECG que consiste en derivar y filtrar pasabajo el ECG. Esta señal se define como f(k) (Figura 2).

La segunda etapa se focaliza en la detección del complejo QRS, lo cual no presenta dificultades particulares cuando la onda R representa la onda elemental del ECG. Adicionalmente el algoritmo usa esta característica para detectar las extremos de la señal filtrada (f(k)) con la ayuda de un filtro adaptativo. A partir de estos puntos el algoritmo busca los dos extremos locales que rodean a cada uno de los extremos. La detección de la onda T constituye la última etapa. Para realizar esta operación se define una ventana de búsqueda a partir de la posición del pico de la onda R. La dimensión de esta ventana está en función de la duración del intervalo RR promedio.

El principio, consiste en buscar los valores más altos de la pendiente (extremos de f(k) dentro de la ventana definida. Estos valores se reagrupan por pares (máximo, mínimo) ó (mínimo, máximo). En el caso más simple, una onda T monofásica, el máximo de la onda T está definido por el cruce por cero entre dos valores de un par. Finalmente, el fin de la onda T está definido por el cruce de f(k) por un umbral definido a partir del segundo valor del par de valores extremos.

La primera observación sobre este algoritmo es que presenta muchas aproximaciones subjetivas, pues las búsquedas de los diferentes puntos cruciales se basan en el establecimiento de umbrales aproximados. Adicionalmente, antes de alcanzar los puntos de interés es necesario detectar varios puntos intermedios. El segundo problema de este algoritmo está relacionado con el pre-filtrado, en efecto, el filtro pasabajo elimina frecuencias significativas de la onda T, que puede inducir problemas no despreciables en la detección de la onda T, cuando no es muy pronunciada. No obstante, para señales que no implican grandes dificultades, la eficacia del planteamiento completo permite acercarse sensiblemente de las posiciones reales y las posibles variaciones de la línea de base no afectan, puesto que son eliminadas por el diferenciador.

En conclusión, este algoritmo implica numerosos criterios subjetivos, pero en contrapartida es simple de aplicar en la medida en que la mayoría de los puntos característicos son definidos como cruces por cero de la señal filtrada.

1.2. Algoritmo basado en la descomposición de ondículas (D2)

La transformada en ondículas es una transformación que divide una señal en sus componentes a distintas escalas tiempo-frecuencia. El segundo detector (D2) utiliza una aproximación multi-resolución basada en ondículas de tipo spline cuadrático (Figura 3). Las ondas P, T y el complejo QRS son de duraciones estadísticamente diferentes y ocupan en el espacio transformado escalas que sólo se solapan parcialmente [6], [7]. El seguimiento de los extremos locales así como los cruces por cero de la descomposición de un nivel de resolución a otro permite localizar los componentes de la señal ECG. Naturalmente, los extremos locales corresponden a las pendientes más fuertes presentes en la señal y los cruces por cero a los extremos locales de la señal.

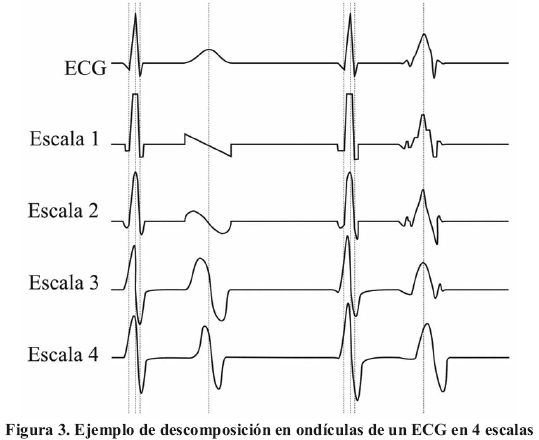
Aplicación del algoritmo: La señal ECG se dividió en seis niveles de detalle. El primer nivel presenta muy poca información vinculada a la señal útil, no se explota para la localización de las ondas de interés. En las otras escalas, se detectan los cruces por cero así como un máximo local y un mínimo local asociado. El seguimiento de estas cinco posiciones temporales, de las
escalas de análisis más gruesas a las más finas, permite localizar el complejo QRS y la onda T.

Por lo tanto, el algoritmo D2 utiliza el mismo tipo de caracterización que el algoritmo D1. Pero permite liberarse del ruido de altas frecuencias presente sobre las escalas bajas. La dificultad de este método reside en el seguimiento de los extremos locales a través de las escalas.

1.3. Algoritmo basado en la Modelización de la onda T D3.

El tercer detector (D3) utiliza un modelo fisiológico de la fase de repolarización ventricular [8]. El algoritmo se divide en tres partes (Figura 4). La primera parte consiste en establecer la ventana de modelización a partir de la detección del complejo QRS y el punto J. En la segunda parte, la onda T se modela a partir de la modelización de dos PA. Ésta se efectúa sobre la porción de señal que sigue un complejo QRS y que contiene enteramente la onda T. Los parámetros del modelo son estimados por un algoritmo de optimización no lineal por medio de la minimización del error cuadrático medio. En la tercera parte del algoritmo se determinan los puntos característicos de la onda T a partir de la primera y la segunda derivada de la señal modelada. Lo que equivale a efectuar la detección de los cruces por cero para localizar los puntos correspondientes a Tmax y a Tfin.

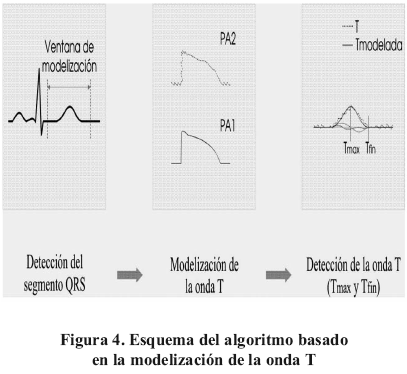
Este método permite efectuar la segmentación de la onda T directamente sobre la señal modelada, eliminando así las imprecisiones debidas al ruido en la localización de los puntos característicos. La dificultad de este algoritmo de segmentación reside en la estimación de los parámetros del modelo.

Aplicación del algoritmo: Para la aplicación de este algoritmo, es necesario detectar la onda R como punto de referencia. El tamaño de la ventana de modelización de la onda T se estableció según la relación presentada sobre la Figura 4, donde el valor del intervalo RR se expresa en ms.

Para las frecuencias cardíacas entre 46 (latidos por minuto /bpm) y 100 bpm, se utilizó una fórmula basada en la corrección de Bazett. Para los otros casos: frecuencias cardíacas menores que 46 bpm o mayores que 100 bpm, se aplicó una corrección lineal. Por último, en el caso de no convergencia del algoritmo, el tamaño de la ventana se establece manualmente.

2. Validación

Los tres algoritmos se implementaron en Matlab. Se llevaron a cabo dos estudios el primero sobre ECG simulados y el segundo sobre señales electrocardiográficas reales.

2.1. ECG simulados

el tipo de ruido y perturbaciones a los cuales deben enfrentarse los algoritmos, así como también la energía de estos ruidos con relación a la señal útil. Este trabajo se basó principalmente en los trabajos de Tikkanen [9] y Porta [10] para la escogencia de los 4 ruidos simulados. La medida clásica de la Relación Señal a Ruido (SNR) en el caso de una señal electrocardiográfica, consiste en calcular el nivel del ruido, sobre el intervalo PR, evaluando el valor cuadrático medio (RMS). Este coeficiente da una medida precisa de la contribución del ruido sobre el ECG, ya que se basa en la
siguiente consideración fisiológica: no existe actividad eléctrica durante la conducción del estímulo ventricular auricular, representado sobre el ECG como la distancia PR. La cantidad RMS da una medida precisa del ruido y teniendo en cuenta la amplitud del QRS, permite una estimación correcta del SNR. Es un cálculo fácil a efectuar, pero presenta el inconveniente de requerir una determinación exacta del segmento PR, tarea que se vuelve delicada al esfuerzo, cuando se acorta este segmento. Como alternativa, se utilizó un método basado en una descomposición en valores propios. Callaerts [11] puso de manifiesto que la descomposición en valores singulares es una herramienta robusta para extraer las señales deseadas de datos con efectos sonoros. Este método se utilizó para medir el SNR sobre señales ECG reales, con el fin de caracterizar la situación deruido a la cual se enfrentan los algoritmos de detección. Elmétodo se validó sobre señales simuladas con resultados juzgados satisfactorios, se obtuvo un error medio de estimación, en valor absoluto, de menos de 10%. Las medidas efectuadas sobre ECG reales condujeron a retener un intervalo entre 10 y 25 dB para evaluar los tres métodos de detección.

2.1.1. Estudios sobre las señales simuladas

Se tomaron el sesgo (ms) y el error cuadrático medio (ms2) como criterios de evaluación. Tomando en cuenta la dificultad del problema, el estudio se limitó a las ondas monofásicas.

2.1.2. Simulación de señales ECG

Se obtuvo una señal ECG sintética repitiendo 400 veces un ciclo cardíaco sin ruido (RR=570ms) muestreado a 1KHz. Esta señal ECG fue corrompida por 4 tipos de ruido:

1) Ruido electromiográfico EMG (Tipo I): simulado a partir de un ruido blanco centrado. Se hizo variar su amplitud hasta un 4% de la amplitud de la onda Tmax lo que corresponde aproximadamente a un SNR de 10 dB.

2) Artefactos debido al movimiento (Tipo II): se simularon a partir de un filtrado pasabanda (3-5 Hz) de un ruido blanco centrado. Se hizo variar la amplitud hasta un 60% de la amplitud de la onda Tmax lo que corresponde aproximadamente a un SNR de 10 dB.

3) Artefactos debido a la respiración (Tipo III): se simularon a partir de un filtrado pasabajo (0.5 Hz) de un ruido blanco centrado. Se hizo variar la amplitud hasta un 60% de la amplitud de la onda Tmax, lo que corresponde aproximadamente a un SNR de 10 dB.

4) Ruido global (Tipo IV): definido como la suma de las 3 fuentes de ruido anteriores.

Para cada tipo de ruido, se generaron cuatro señales con SNR de 10, 15, 20 y 25 dB.

Por último, cada señal fue segmentada por los tres métodos propuestos.

Nota: el nivel del ruido (en dB) es susceptible de generar distintas gamas de variabilidad, y por lo tanto de influenciar de forma diferente la medidas del intervalo RT. Se constató por ejemplo que el ruido de Tipo II a 15 dB perturba evidentemente la forma de la onda T mientras que el ruido de Tipo III a 15 dB prácticamente no afecta la forma de la onda T (Figura 5).

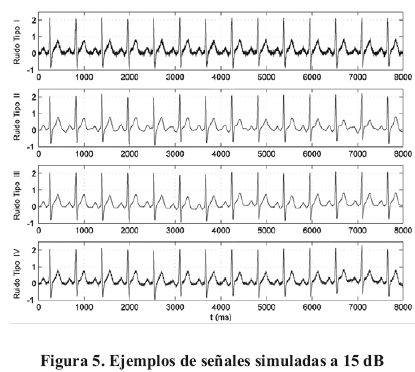
2.1.3. Resultados sobre señales simuladas

Las Tablas I y II presentan los resultados de la evaluación de los algoritmos sobre las señales simuladas. En general, se observa que los algoritmos de detección D1 y D3 detectan todas las ondas T a diferencia de detector D2. Este último no detecta seis ondas T en el caso de un ruido de tipo II y para el SNR más desfavorable (10 dB) y olvida una onda T en el ruido tipo IV a 10 dB. No hubo ninguna falsa detección. Se observa en general un sesgo muy pequeño para D1 excepto en los casos muy desfavorables de los ruidos de tipo II y tipo IV a 10 dB.

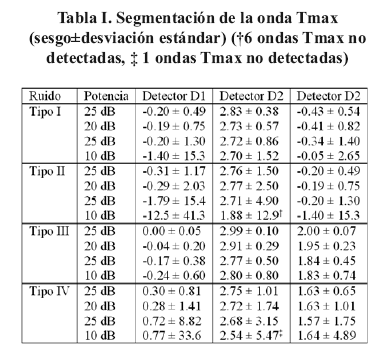
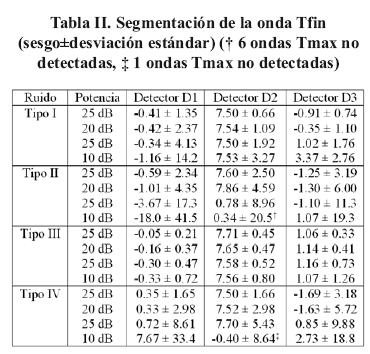
El detector D3 proporciona globalmente valores de sesgo ligeramente más elevados para la detección de Tmax y Tfin (ruidos tipos III y IV) pero también ofrece una mayor robustez. La misma robustez puede constatarse, en un grado menor, en el detector D2 (excepto para el ruido de tipo II a 10 dB).

Sin embargo, este detector proporciona instantes de detección sesgados (alrededor 2.8ms para Tmax y 7.5ms para Tfin). Además estos valores son estables en cualquiera situación de ruido y/o potencia, lo que sugiere que el sesgo sea inherente al método.

Por lo tanto, los valores del sesgo son relativos a la definición empleada por cada algoritmo y deben ser comparados con la diferencia que cometerían sistemáticamente 2 lectores expertos [5]. A continuación se presenta un análisis detallado para cada tipo de ruido.

Ruido Tipo I: para SNR superiores a 15 dB se constatan resultados similares entre los detectores D1 y D3 para la detección de Tmax. Los valores de desviación estándar son pequeños (> 2 ms) pero aumentan a medida que el SNR disminuye (de 0.5 ms 25 dB a 1.4 ms a 15 dB). En este rango, los resultados de D3 son ligeramente mejores, puesto que la desviación estándar aumenta sólo de 0.38 ms 25 dB a 0.86 ms a 15 dB. Por el contrario cuando el SNR es bajo (10 dB), los resultados de D1 se deterioran radicalmente: la desviación estándar se aumenta 10 veces para alcanzar los 15 ms, mientras que los otros dos detectores presentan aún resultados aceptables (inferior a 2.7 ms para Tmax e inferior a 3.5 ms para Tfin). Esta degradación significativa del detector D1 a 10 dB se encuentra sobre la determinación de la posición del Tfin. En cuando a la detección de Tfin, se constata que los detectores D2 y D3 proporcionan resultados similares en término de desviación estándar, 2 veces más pequeña que para D1 (SNR ≥ 15 dB). Por el contrario, existen diferencias en
términos de sesgo, el sesgo del detector D2 es estable mientras que el sesgo del detector D3 varía de -1 ms 25 dB a 3.4 ms a 10 dB.

Ruido Tipo II: se constata que esta fuente de ruido afecta substancialmente los resultados de los algoritmos. Las degradaciones se observan a partir de un SNR de 15 dB. En condiciones más favorables, los valores de desviación estándar son claramente superiores a los obtenidos con el ruido anterior, aproximadamente de 2 ms contra 0.8 ms para Tmax y entre 4.5 y 6 ms contra 1 a 2 ms para Tfin. Las degradaciones a 15 dB son especialmente más sensibles para el detector D1, los valores de desviación estándar son aproximadamente de 15 ms para Tmax y 17 ms para Tfin. Sin embargo, el sesgo de D2 para la detección de Tfin a 15 dB no es estable (sesgo de 0.78 ms para una desviación estándar de 9 ms en vez de un sesgo promedio de 7.5 ms) lo que advierte la degradación de los resultados de este método. A 10 dB, el detector D2 deja de detectar algunas ondas T, contrariamente a los otros detectores. Al mismo tiempo, el detector D3 ofrece resultados robustos para Tmax (el sesgo es casi nulo y la desviación estándar sólo es de 5 ms) y aceptables para Tfin (el sesgo es de 1 ms y desviación estándar de 20 ms).

Ruido Tipo III: esta fuente de ruido prácticamente no afecta los resultados de ningún detector En efecto, aunque se constata que la desviación aumenta con la disminución del SNR, los valores máximos obtenidos no exceden nunca 1 ms.

Ruido Tipo IV: en general, los efectos del ruido de Tipo II prevalecen con relación a los otros. Así hasta 20 dB, los 3 métodos presentan resultados similares. A continuación a 15 dB, los resultados de D1 comienzan a deteriorarse para la detección de Tmax, al igual que D1 y D3 para la determinación de Tfin. Por el contrario a 10 dB, los resultados de D3 siguen siendo aceptables y los detectores D1 y D2 presentan no detecciones y valores elevados de sesgo y desviación estándar).

Los resultados ponen de manifiesto que los resultados del detector D1 se deterioran seriamente en cuanto las ondas T son de poca energía y que el SNR bajo (10 dB). Estos resultados confirman la poca robustez del método de la derivada filtrada a un ruido de origen de alta frecuencia (HF) como es el caso del ruido de Tipo I. Por el contrario, se constata que el detector D2 es mucho más robusto a este Tipo de ruido. Este ruido está en efecto muy presente sobre las escalas finas (escalas 1 y 2) y ausente en las escalas más gruesas, lo que permite una buena detección.

Por último, el detector D3, presenta resultados similares al algoritmo de los ondículas y da buenos resultados en condiciones desfavorables de SNR. Además, los detectores son más sensibles y menos robustos ante el ruido de Tipo II, ya que este último ocupa la misma banda de frecuencia que la onda T. A 10 dB, D3 es el más robusto. Hay que señalar que contrariamente al ruido Tipo I, el ruido Tipo II no puede ser filtrado por la descomposición en ondículas. Las no detecciones observadas sobre el detector D2 resultan de una dificultad del algoritmo de aislar los puntos singulares de la señal, ya que estos últimos se encuentran deformados por el ruido.

Estos resultados indican que el detector D3 presenta globalmente los resultados más robustos, aunque son comparables a los obtenidos por el detector D2. Este último método presenta dificultades en la definición de los puntos singulares, cuando el ruido presente ocupa la misma banda de frecuencia que la onda T.

2.2. Resultados sobre señales reales

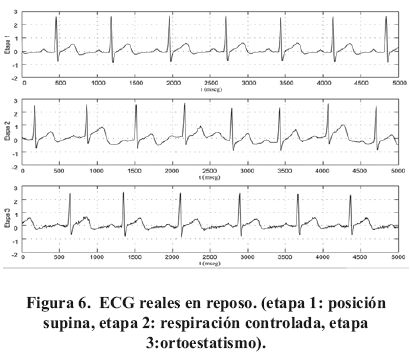
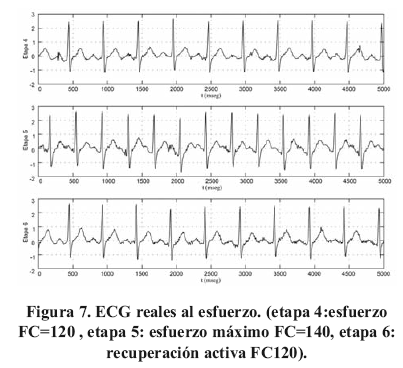
Un registro ECG del protocolo descrito en [12] fue anotado por dos lectores expertos (L1 y L2) y segmentado con los tres algoritmos. El registro consta de 3 sub-registros (etapas) ECG de reposo (etapa 1: posición supina, etapa 2: respiración controlada, etapa 3:ortoestatismo) y 3 etapas ECG en esfuerzo (etapa 4:esfuerzo, frecuencia cardiaca/FC=120 bpm, etapa 5: esfuerzo a FC=160 bpm, etapa 6: recuperación activa a FC=120 bpm). El ECG fue adquirido a 1Khz, cada etapa tiene una duración de dos minutos. En las Figuras 6 y 7, se observan los cinco primeros segundos de cada etapa.

El ECG de la segunda etapa ilustra las modificaciones que sufre la onda T debido a la respiración, igualmente se observan deformaciones al esfuerzo de la onda T y un aumento del ruido de alta frecuencia.

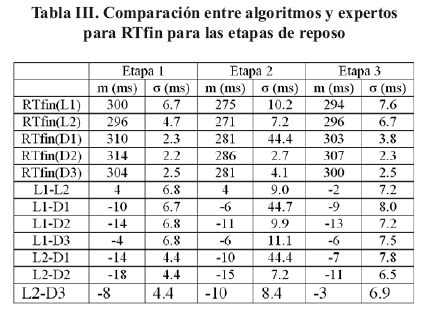
Los sesgos y desviaciones estándares de RTfin y RTmax se calculan a partir de las anotaciones de dos lectores expertos (L1 y L2). Las medidas manuales se efectuaron sobre un papel milimetrado donde 1 mm horizontal correspondiente a 50 mm/s, es decir que el error de medida manual es de 20 ms. Los resultados se presentan en las Tablas III y IV para los registros de reposo y en las Tablas V y VI para los registros al esfuerzo. Se observa que las variaciones entre los expertos y los tres métodos automáticos son equivalentes e inferiores a 20 ms. En todos los casos las desviación estándar de de RTfin et RTmax, medidas manualmente, son inferiores al error de medida, con la excepción del detector D1 en la etapa 2. Esto puede deberse a los cambios morfológicos de la señal. Se puede observar que el ruido que afecta el ECG en esta etapa es esencialmente de Tipo III; es la superposición de un ruido Tipo II, lo que afecta los resultados de detección. Sin embargo,
la energía de este ruido no es lo suficientemente importante para perturbar al detector D2, aunque este detector presenta dos no detecciones en la etapa 5. En esta etapa se observa claramente la degradación de la forma de la onda T, se puede suponer que el fin de la onda será mucho más difícil de determinar. Adicionalmente esta onda se encuentra atenuada y contaminado por un ruido de alta frecuencia (HF). Los resultados muestran que efectivamente hay una gran variabilidad en Tfin en esta etapa; uno de los expertos (L2) juzga que la mitad de los latidos en esta etapa no son anotables (Tabla VII).

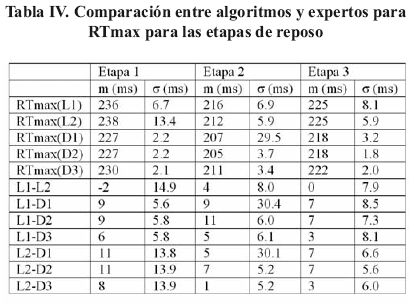
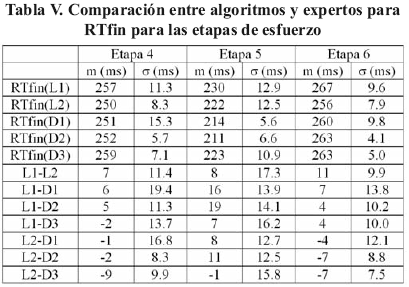
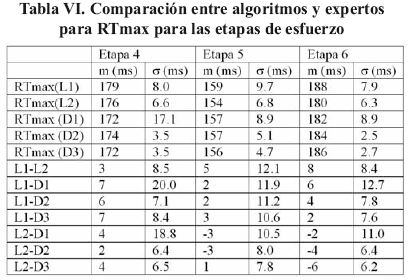
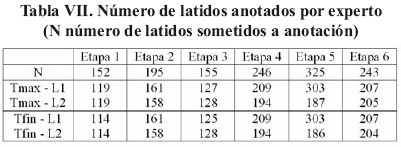
En general la variabilidad obtenida por medios automáticos es significativamente más pequeña que la obtenida manualmente. Sobre medidas manuales está reportado que la variabilidad intra-lector es de 6 ms y la variabilidad interlector va de 7 a 20 ms en función de la frecuencia cardíaca
[13][14]. Es necesario señalar también que los resultados fueron obtenidos con un único juego de parámetros por método. Como los usuarios de estos métodos no son generalmente las personas que las aplican, no se optimizaron los juegos de parámetros de los métodos para cada una de las
condiciones experimentales.

III. CONCLUSIONES

1. Los resultados obtenidos muestran comportamientos satisfactorios de los tres enfoques sobre ECG poco ruidosos.

2. Los resultados sugieren que con la disminución de la SNR el detector basado en ondículas (D2) y el detector basado en la modelización (D3) presentan los mejores resultados.

3. Además, los resultados al esfuerzo confirman que el detector D3 presenta resultados más estables.

4. Las simulaciones permitieron comparar y validar los métodos de segmentación automática latido a latido muy sensibles al ruido y más concretamente al ruido que se encuentra en la banda de frecuencia de 3 a 5 Hz.

5. Es importante observar que el ruido introducido en estas simulaciones induce una variabilidad no fisiológica. Por ejemplo, la variabilidad de los intervalos RTmax y RTfin medida con el detector D3 es de 2 ms y 10 ms respectivamente para el ruido de tipo IV a 15 dB.

6. Es decir, según la potencia del ruido, la variabilidad inducida por esta fuente no fisiológica puede ser comparable a la observada.

7. De manera general, el intervalo RTmax proporcionó los resultados más confiables en todas las situaciones.

8. La extracción de los parámetros resultantes de las seriesde intervalos RT constituye la primera etapa para estudiar la variabilidad de la repolarización.

IV. REFERENCIAS

 1. Haverkamp,. W., et, al. The Potential for QT Prolongation and Pro-Arrhythmia by Non-Anti-Arrhythmic Drugs: Clinical and Regulatory Implications, Report on a Policy Conference of the European Society of Cardiology. Cardiovasc Res, 2000.  47 ( 2): 219-33.         [ Links ]

2. Malik  M,  Camm, A. J. Evaluation of Drug-Induced QT Interval Prolongation: Implications for Drug Approval  and Labeling. Drug Saf. 2001, 24 ( 5): 323-51.        [ Links ]

3. Macfarlane, PW., Latif. S. Automated Serial ECG Comparison Based on the Minnesota Code. J. Electrocardiol, 1996. 29 ( Suppl): 29-34.         [ Links ]

4. Merri  M,. et al. Relation between Ventricular Repolarization Duration and Cardiac Cycle Length During 24-Hour Holter Recordings. Findings in Normal Patients and Patients with Long QT Syndrome. Circulation, 1992. 85 ( 5): 1816-21.        [ Links ]

5. Laguna,. P. et al. Algorithm for QT Interval Analysis in 24-hour Holter ECG: Performance and Applications. Med Biol Eng Comput.    1990. 28 (1): 67-73.        [ Links ]

6. Li,. C., Zheng,. C., Tai,. C. Detection of ECG Characteristic Points Using Wavelet Transforms,. IEEE Trans Biomed Eng. 1995. 42 (1): 21-8.        [ Links ]

7. Sahambi,. J. S., Tandon,. S. N., Bhatt,. R. K. An Automated Approach to Beat-by-Beat QT-Interval Análisis. IEEE Eng Med Biol Mag.  2000.  19 (3): 97-101.        [ Links ]

8. Vila,. J., et,. al. 2000. A New Approach for TU Complex Characterization. IEEE Trans Biomed Eng. 2000. 47 ( 6): 764-72.         [ Links ]

9. Tikkanen,. PE., et,. al. Using Simulated Noise to Define Optimal QT Intervals for Computer Analysis of Ambulatory ECG. Med Eng Phys.,  1999.  21 ( 11): 15-25.        [ Links ]

10. Porta. A., et al. Performance Assessment of Standard Algorithms for Dynamic R-T Interval Measurement: Comparison between R-T Apex and R-T end Approach. Med. Biol. Eng. Comput.  1998. 36 ( 1): 35-42.         [ Links ]

11. Callaerts,. D., et,. al. Comparison of SVD Methods to Extract the Foetal Electrocardiogram from Cutaneous Electrode Signals. Med Biol Eng Comput. 1990.  28: 217-24.        [ Links ]

12. Wong  S., et al., Multiple Factor Analysis as a Tool for Studying the Effect of Physical Training on the Autonomic Nervous System. Proceeding Computers in Cardiology. IEEE Computer Society Press, 2002.         [ Links ]

13. Murria,. A., et,. al. Furniss SS and Campbell RW. Errors in Manual Measurement of QT Intervals. Br. Heart J. 1994. 71 ( 4): 386-90.        [ Links ]

14. Savelieva,. I., et,. al. Relation of Ventricular Repolarization to Cardiac Cycle Length in Normal Subjects, Hypertrophic Cardiomyopathy, Patients with Myocardial Infarction. Clin Cardiol. 1999.  22 ( 10): 649-654.          [ Links ]