CÁLCULO DE LA VECINDAD MEDIANTE GRAFOS EN MINERÍA DE TEXTOS

Artigas Fuentes, Fernando Gil García, Reynaldo Badía Contelles, José Manuel Pons Porrata, Aurora

El MSc. Fernando Artigas Fuentes es Profesor Asistente en el Centro de Estudios de Reconocimiento de Patrones y Minería de Datos (CERPAMID) Facultad de Matemática y Computación, Universidad de Oriente, Patricio Lumumba S/N, Santiago de Cuba, telef. (53) 22-635346, correos electrónicos artigas@csd.uo.edu.cu  y artigas@cerpamid.co.cu.

El Dr. Reynaldo Gil García es Profesor Auxiliar en el mismo Centro, mismo teléfono, correos electrónicos gil@csd.uo.edu.cu  y gil@cerpamid.co.cu.

El dr. José Manuel Badía Contelles es Profesor Titular en el Dpto. de Ingeniería y Ciencia de los Computadores, Universidad Jacume I, Av. Los Baynat s/n, 12071, Castellón, España, Teléfono (34) 964728281, correo electrónico badia@icc.uji.es.

La Dra. Aurora Pons Porrata es Profesora Titular en el CERPAMID, misma dirección y teléfono ya citados, correos electrónicos aurora@csd.uo.edu.cu  y aurora@cerpamid.co.cu .

Resumen:

La búsqueda de los documentos más semejantes a uno dado es fundamental en la Minería de Textos, pues es el procedimiento básico de muchas técnicas como la clasificación o la recuperación de información. Los documentos suelen representarse en un espacio de rasgos de alta dimensionalidad, donde cada término que ocurre en el documento se trata como un rasgo y el peso de cada término refleja su importancia en el documento. Existen multitud de técnicas para buscar la vecindad de un objeto, pero disminuyen drásticamente sus prestaciones a medida que crecen las dimensiones. Este problema imposibilita su aplicación al caso de los documentos. En este artículo se presenta un método de acceso basado en una estructura de grafo que determina de forma aproximada la vecindad de un nuevo documento. El método obtenido presenta una selectividad alta y una tasa de error aceptable cuando se usa embebido en un clasificador, comparándolo con el método exhaustivo que evalúa el 100% de los documentos. Como resultado del estudio se concluye que es factible el uso del método propuesto en problemas de muy alta dimensionalidad, como es el caso de la Minería de Textos.

 Palabras clave: Minería de datos/ Minería de textos/ Métodos de acceso/ Indexado en muy alta dimensionalidad/ Cálculo de la vecindad.

VICINITY CALCULATION WITH GRAPHS IN TEXT MINING

Summary:

Searching the most similar documents to a given one is crucial in Text Mining because it is the basic process of many techniques like classification or information retrieval. The documents are usually represented in high-dimensional feature space, where each term appeared in documents is treated as features and the weight of each term reflects its importance in the document. There are many approaches to find the vicinity of an object, but their performance drastically decreases as the number of dimensions grows. This problem prevents its application for documents. In this paper, we present an access method based on a graph structure that determines in an approximate way the vicinity of a novel document. The obtained method has a high selectivity and an acceptable error rate when it is embedded in a classifier and compared with the exhaustive method that evaluates all documents. Our experimental analysis shows that it is feasible the use of the proposed method in problems of very high dimensionality, such as Text Mining.

Keywords: Data Mining/ Text Mining/ Access Methods/ Very high-dimensional indexing/ Neighborhood calculation.

Manuscrito finalizado en Santiago de Cuba, el 2008/01/10, recibido el 2008/02/07, en su forma final (aceptado) el 2008/03/10.

I. INTRODUCCIÓN

La búsqueda de los documentos más semejantes a uno dado es fundamental en la Minería de Textos, pues es el procedimiento básico de muchas técnicas como la clasificación o la recuperación de información. Los documentos suelen representarse en un espacio de rasgos de alta dimensionalidad, donde cada término que ocurre en el documento se trata como un rasgo y el peso de cada término refleja su importancia en el documento. Debido a los grandes volúmenes de información textual existentes en la actualidad y a que el cálculo de las semejanzas entre documentos es un proceso muy costoso dada su alta dimensionalidad, la reducción drástica del número de semejanzas calculadas durante este tipo de búsquedas reviste una importancia crucial.

En la literatura aparecen numerosas propuestas de métodos de acceso a objetos multidimensionales, que los organizan de  algún modo, garantizando que dado un objeto de consulta puedan recuperarse los objetos más relacionados con éste, usando un determinado criterio de comparación (más cercanos, más semejantes, etc.). Los objetos así obtenidos son conocidos como la vecindad del objeto de consulta.

Un tipo especial de método multidimensional es el basado en espacios métricos. La mayoría de los métodos de este tipo propuestos en la literatura sufren el problema conocido como “maldición de la dimensionalidad” [1], que consiste en que cuando se incrementa el número de dimensiones del espacio de representación de los objetos, disminuye drásticamente la selectividad o se incrementa el tiempo de procesamiento, por lo que empeoran sus prestaciones. Entre estos métodos se tiene la familia M-tree [2], que disminuye drásticamente sus prestaciones a partir de 25 dimensiones.

Para resolver el problema de la maldición de la dimensionalidad se han diseñado métodos especiales que lo enfocan de diversas maneras. En 1996 Dickerson [3], propuso un método basado en un grafo o malla conexa, construida mediante una variante del método de triangulación de Delaunay [4], con todos los objetos que forman parte del problema. En esta malla cada objeto queda conectado con aquellos que se encuentran más cercanos a éste en el espacio de representación. Pero esta estructura se usa sólo para encontrar la vecindad de los objetos que forman parte de ella. Además, en el caso de los documentos, tampoco es posible utilizar el método de Delaunay, debido a que lo común en la MT es contar con más dimensiones que documentos y este método requiere precisamente lo contrario. En 1997 Nene y Naya [5], propusieron una variante de un método de Friedman [6], para encontrar el vecino más cercano, que se basa en la construcción de una estructura de datos, en la que se almacenan algunos datos precalculados que luego van a ser usados para las búsquedas, evitando que sean calculados en ese momento.

La construcción de esta estructura es costosa en tiempo, pero se realiza una sola vez. Para su construcción se ordenan los objetos por la primera dimensión y durante la etapa de búsqueda, los objetos candidatos a solución son aquellos que están encerrados entre un conjunto de hiperplanos, calculados para esa dimensión según la consulta. Luego se sigue un proceso de descarte para el resto de las coordenadas. Este algoritmo resulta costoso en tiempo cuando el número de las dimensiones es muy alto. Otras propuestas más recientes, como son el VA-file [7], y el IQ-tree [8], consideradas como métodos de compresión, mantienen buenas prestaciones hasta dimensiones mucho mayores; han sido probadas por sus autores hasta 500 dimensiones, pero siguen siendo métodos de búsqueda exhaustiva, aunque usan espacios de representación más simples.

El IQ-tree se comporta mejor que el VA-file, pero para espacios de sólo unas decenas de dimensiones. Otra vía propuesta en la literatura ha sido reducir la dimensionalidad del espacio, aplicando diferentes técnicas de selección de rasgos [9] [10],, hasta un valor apropiado que permita aplicar las técnicas existentes. Actualmente se trabaja en el desarrollo de algoritmos más eficientes de búsqueda de los k-vecinos más cercanos que reduzcan el porcentaje de distancias calculadas, pero estos trabajos se centran en espacios de hasta algunos centenares de dimensiones [11] [12]. En este artículo se propone un método de acceso con una estructura de indexado en forma de grafo que permite determinar en forma aproximada la vecindad de un documento dado como consulta. Este método se usa en clasificación supervisada, y presenta buenas prestaciones para espacios de muy alta dimensionalidad (decenas de miles de dimensiones).

El método reduce drásticamente la cantidad de semejanzas calculadas para obtener la vecindad de un documento mientras la calidad de la clasificación es similar a la obtenida con la búsqueda exhaustiva de la vecindad. El trabajo está organizado como sigue: en el desarrollo se muestran las principales ideas usadas para el diseño del método propuesto, se describen la estructura de datos y los algoritmos de búsqueda propuestos, así como los experimentos realizados para evaluar sus prestaciones. Luego se presenta un análisis de los resultados obtenidos y finalmente se dan las conclusiones a este trabajo.

II. DESARROLLO

1. Materiales y métodos

1.1 Componentes de los métodos de indexado y características deseadas

Los métodos de indexado están formados por dos componentes: la estructura de indexado, que determina la organización de los datos y la estrategia de búsqueda, que determina el algoritmo con el que se recorre la estructura de indexado. La estructura de indexado puede ser un arreglo, una lista, un árbol, un grafo (que es el que se usa en esta propuesta), etc., o cualquier combinación de éstas. Las principales estrategias de búsqueda reportadas en la literatura son: la exhaustiva (tomada como referencia para el resto de los métodos), con particionamiento [13] con múltiples etapas [14]., Omni [15], aproximada [16] y búsqueda en el espacio de solución [17]. En el presente caso, se propone una estrategia que consta de dos etapas, mezclando una búsqueda exhaustiva en un pequeño conjunto de objetos con la estrategia de mejor en profundidad para obtener una solución aproximada de la vecindad.

Una vez que se selecciona una combinación de estructura de indexado y estrategia de búsqueda, se espera que el método formado cumpla con la mayoría de las propiedades siguientes:

• Alta capacidad de página: que la cantidad de objetos que pueden ser almacenados en un tamaño determinado de memoria sea máxima.

• Alta selectividad: que un elevado porcentaje de objetos que no pertenecen a la solución de una consulta no sean visitados durante las búsquedas. • Comportamiento escalable en cuanto a la dimensionalidad: que no empeoren las prestaciones a medida que crece el problema a tratar.

• Garantía de que los objetos más semejantes se encuentren cercanos en la estructura de indexado.

• Facilidad de paralelización: debido a que, por lo general, los problemas tratados son de gran tamaño y es deseable aprovechar la potencia de cálculo de las arquitecturas paralelas. En Minería de Textos es usual comparar dos documentos di,dj utilizando la medida de semejanza del coseno. Como el método propuesto se basa en un espacio métrico se necesita una función de distancia, que puede obtenerse como el dual de la semejanza coseno mediante la expresión:

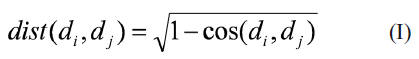
donde la función coseno se calcula de la siguiente forma:

 

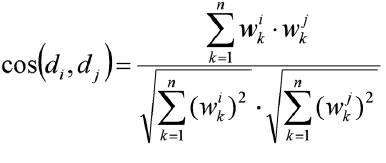
donde n es el número de términos (dimensiones) del espacio de representación w_ik y w_jk son los pesos del término k en los documentos d_i y d_j, respectivamente.

Esta función de distancia retorna valores entre 0 y 1. El valor 0 se corresponde (al ser el dual de la semejanza) con la máxima semejanza entre los objetos, mientras que el valor 1 se corresponde con la mínima. Usualmente, a partir de un documento de consulta se desea conocer de su vecindad los primeros k-vecinos (k-NN) en orden decreciente de semejanza (o creciente de distancia) y los vecinos que se encuentran a menos de un radio dado (o con semejanza mayor que un umbral), entre otros casos. En el apartado siguiente se explica cómo se construye la estructura de indexado y cómo a partir de un documento de consulta se calcula su vecindad.

1.2. Método de acceso propuesto

Al igual que otros métodos, en este caso se cuenta con dos conjuntos de documentos, el primero, y más pequeño (E), es conocido como conjunto de entrenamiento y es usado para construir la estructura de indexado; el segundo (T), que cuenta con un enorme volumen de documentos, es usado como consulta o conjunto de prueba. De los métodos descritos se ha utilizado la idea del uso de un grafo y de dividir el problema en dos etapas: construir primero la estructura de indexado con el conjunto de entrenamiento de modo offline y una sola vez, por lo que no importa su costo en tiempo, y realizar las consultas (o búsquedas) online tantas veces como se requiera y con el menor costo en uso de CPU y tiempo posibles, reduciendo el número de distancias entre documentos calculadas. Otra idea aplicada es el uso de centroides de grupos de documentos como pivotes durante la construcción de la estructura. Un centroide , es el documento representativo de un conjunto de documentos X. Éste puede ser calculado de distintas formas, por ejemplo, como el vector suma de todos los documentos del conjunto. En ese caso cada componente se calcula como:

 

donde w_ik se corresponde con el peso del término k en el documento

Si el conjunto X está constituido sólo por dos documentos {d_p, d_q}, por comodidad en la notación, en lugar de

La idea general del método propuesto es la siguiente: construir a partir de los documentos del conjunto de entrenamiento un grafo conexo contenido en un hiper-anillo, con centro en el centroide del conjunto y con dos bordes: uno interior, alrededor del centroide y formado por una selección de los documentos más cercanos a éste; y otro exterior, formado por una selección de los documentos más alejados de él. La fase de consulta se realiza en dos etapas. En la primera se determina, usando el método exhaustivo, cuál de los documentos que pertenecen a los bordes es el más cercano al documento de consulta. Este documento se toma como punto de entrada a la estructura y utilizando el criterio del mejor en profundidad se sigue un proceso de selección y descarte de documentos hasta que se obtiene el vecino más cercano. El proceso se detiene cuando no es posible seguir avanzando en la estructura sin alejarse del documento de consulta. El vecino más cercano encontrado pudiera ser el verdadero o una aproximación. Si se desea que la respuesta a la consulta contenga más documentos se aplica una última fase de búsqueda (kNN). Partiendo del vecino más cercano encontrado en la etapa anterior, se explora el grafo siguiendo una estrategia de primero en profundidad y se va construyendo el conjunto solución agregando nuevos documentos cercanos al de consulta hasta que se obtengan en un número de k , ordenados en orden creciente de distancia. A partir de estas ideas, las hipótesis que serán comprobadas con el método propuesto son:

• La suma del número de documentos que pertenecen a los bordes y el número de documentos que es evaluado durante el resto del proceso de búsqueda es menor que el total de documentos en la estructura, en contraposición con el método exhaustivo, que evalúa el 100% de los documentos.

• Si el método se usa embebido en un clasificador de documentos, (que es el objetivo final con que se ha diseñado) los resultados obtenidos en la clasificación son en alto grado semejantes a los obtenidos cuando se usa en las mismas condiciones el método exhaustivo.

1.3 Construcción de la estructura de indexado

La estructura de indexado propuesta es un grafo G=(E,U,C,B), donde los vértices son los documentos del conjunto de entrenamiento E={d1,d2,...,dn}, U es el conjunto de las aristas (relaciones de distancias entre los vértices); C contiene a los centroides de todos los pares de vértices relacionados en U ; y B es el conjunto de los elementos de E que pertenecen a los bordes del grafo. G se obtiene a partir de E y de un valor de conectividad suministrado, mediante la secuencia de pasos siguiente:

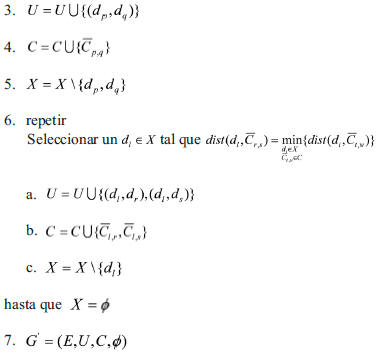
1.4 Estrategia de búsqueda

La estrategia de búsqueda que se sigue para encontrar el vecino más cercano y los k vecinos más cercanos del conjunto de entrenamiento a un documento de consulta se describe en los algoritmos 3 y 4, respectivamente.

2. Resultados

Experimentos realizados

Para comprobar la efectividad del método se tomó como base la colección de documentos Reuters Corpus Versión 1 (RCV1- v2). Esta colección contiene un total de 800000 documentos, clasificados manualmente en 103 tópicos. Se usó la partición LYRL2004 que contiene 23149 documentos de entrenamiento y 781265 documentos de prueba, conformando un espacio de representación de 47152 dimensiones. Para comprobar la selectividad del método propuesto se procedió como sigue:

Experimento 1. Estudio de la selectividad. Se construyeron 6 subconjuntos de entrenamiento de diferentes tamaños, seleccionando el 5, 10, 15, 20, 25 y 30% del conjunto de entrenamiento original, manteniendo la distribución de probabilidades de los tópicos y se construyeron los grafos correspondientes. Se seleccionaron, además, 20000 documentos de prueba de forma aleatoria. Para cada documento de prueba se halló el vecino más cercano utilizando las seis estructuras de indexado creadas. En cada grafo se calculó el porcentaje promedio de distancias calculadas en los documentos de prueba. Utilizando los mismos datos se compararon los vecinos más cercanos de cada documento de prueba obtenidos por el método exhaustivo de búsqueda y el método propuesto, calculando en cada grafo los porcentajes de soluciones exactas obtenidas. Además, se reportó para cada grafo el tiempo promedio consumido por las consultas.

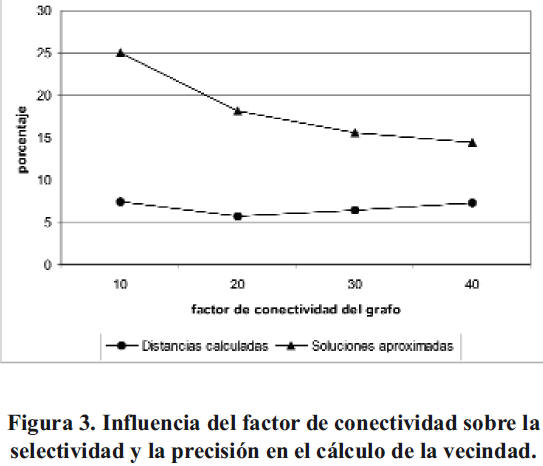
Experimento 2. Estudio del porcentaje de soluciones aproximadas obtenidas en las consultas al variar el factor de conectividad durante la construcción de la estructura de indexado. Se construyó un subconjunto de entrenamiento seleccionando 4000 documentos del conjunto de entrenamiento original. Se seleccionaron, además, 20000 documentos de prueba de forma aleatoria. Se construyeron grafos usando como factor de conectividad 10, 20, 30 y 40. Para cada documento de prueba se halló el vecino más cercano utilizando las cuatro estructuras de indexado creadas. En cada grafo se calculó el porcentaje promedio de distancias calculadas en los documentos de prueba y el porcentaje de soluciones aproximadas obtenidas. Para comprobar si el uso del método propuesto en un problema de clasificación afecta o no la calidad, se procedió como se explica a continuación. Artigas, F. et al. Cálculo de la vecinidad mediante grafos en minería de textos 168

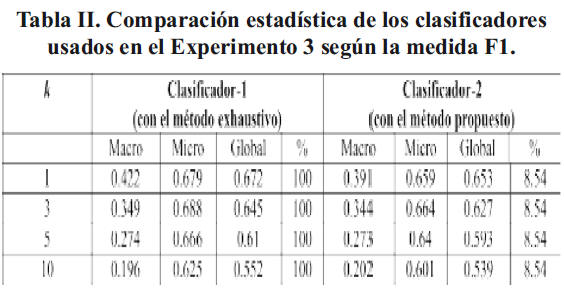
Experimento 3. Aplicación del método a la clasificación de documentos. Se seleccionaron 9884 documentos de entrenamiento (lo que representa el 35% del conjunto original). El espacio de representación de estos documentos es de 31761 dimensiones. Se seleccionaron además 20000 objetos de prueba de forma aleatoria. Para el experimento se usó el conocido clasificador k -NN (18) que asigna el documento de consulta a la clase (o tópico) más votada. Se denominará clasificador-1 al uso en el k -NN del método de búsqueda exhaustivo para la obtención de los k - vecinos más cercanos, y clasificador-2 cuando en su lugar se usa el método de búsqueda propuesto.

En ambos clasificadores se varió el parámetro k en los valores 1, 3, 5 y 10 y se clasificó a los documentos de prueba. Para evaluar la calidad de la clasificación se usaron las tradicionales medidas de Precisión, que mide del total de documentos clasificados la porción que lo fue correctamente; Relevancia, que mide de los documentos pertenecientes a un tópico la porción que le fue asignado; y la medida F1 que es la media armónica de las anteriores. Para obtener la medida F1 sobre todos los tópicos se utilizaron las variantes micro y macro-promediadas, así como la global (19), debido a que los tópicos de la colección utilizada difieren significativamente en tamaño. La medida macro-F1 asigna igual importancia a todos los tópicos, mientras que la micro-F1 y la F1 global asignan una mayor importancia a los tópicos más poblados.

Todos los experimentos anteriores fueron realizados usando implementaciones del método propuesto y del exhaustivo sobre C estándar y compilados con el gcc 4.1.2, sobre un Pentium D a 3.40 MHz y 2 Gb de RAM, con la distribución Gentoo del Linux y el kernel 2.6.23 para 64 bits.

3. Discusión de los resultados

Como resultado del experimento 1 se obtuvieron los datos que se muestran en la Figura 1.

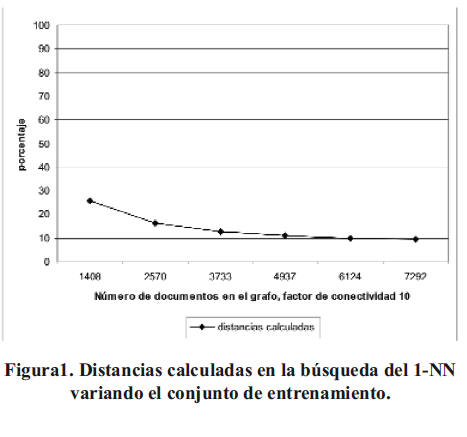
Como se aprecia, a medida que aumenta el número de documentos de entrenamiento en la estructura de indexado, menor es el porcentaje promedio de comparaciones entre éstos y el documento de consulta, llegando a ser menor del 10% cuando contiene aproximadamente 6000 documentos. Por lo tanto, la selectividad del método se incrementa con el aumento del tamaño del conjunto de entrenamiento. Es necesario tener en cuenta de que en este porcentaje se incluye el costo fijo de evaluar todos los documentos que pertenecen a los bordes del grafo. En la Tabla I se muestran los porcentajes de vecinos más cercanos exactos obtenidos por el método propuesto.

Se nota que en todos los casos se obtiene un alto porcentaje de soluciones exactas. Como se muestra en la Figura 2, el tiempo promedio consumido por las consultas se mantiene estable en el método propuesto, siendo menor que para el método exhaustivo a partir de grafos con más de 1000 documentos.

Como resultado del Experimento 2, en la Figura 3 se muestra cómo disminuye el porcentaje de soluciones aproximadas, al aumentar el factor de conectividad del grafo, mientras que el porcentaje promedio de documentos comparados se mantiene relativamente estable.

 

La Tabla II muestra un resumen de los resultados obtenidos en el Experimento 3. Como se aprecia, la calidad de la clasificación obtenida en ambos métodos es similar, con la ventaja adicional de que se reduce sustancialmente el número de comparaciones entre documentos realizadas en el método propuesto y, por tanto, el tiempo necesario para realizar el mismo número de clasificaciones.

Nótese que en los experimentos reportados el porcentaje promedio de distancias calculadas al incrementar el k no varía en el método propuesto. Esto se debe a que la búsqueda de los k vecinos más cercanos (k>1) no implica cálculos adicionales de distancias, porque éstas ya fueron calculadas durante el recorrido realizado en el grafo durante la búsqueda del vecino más cercano. Como resultado del análisis del comportamiento de la selectividad, calidad en la clasificación y costo en tiempo del método propuesto se concluye que es factible su uso en problemas de Minería de Textos que requieran del cálculo de la vecindad de una consulta por semejanza en los rangos de cantidad de objetos de entrenamiento mostrados.

III. CONCLUSIONES

A continuación se resumen las principales conclusiones obtenidas con el método de búsqueda de vecindad propuesto aplicado a la clasificación de documentos. 1. La selectividad crece con la cantidad de documentos presentes en el grafo, llegando a ser del 90% cuando este número llega a 6000, reduciendo drásticamente la cantidad de comparaciones necesarias durante las búsquedas. 2. El costo en tiempo es mucho menor en el método propuesto que en la estrategia de búsqueda exhaustiva a partir de grafos con más de 1000 documentos. 3. El porcentaje de soluciones exactas obtenidas durante las búsquedas es alto y se incrementa con el aumento del factor de conectividad usado en la construcción de la estructura de indexado. 4. La calidad de la clasificación obtenida para la colección Reuters (RCV1-v2), usando el método propuesto, es similar a la obtenida con el método exhaustivo. 5. Resulta factible el uso del método propuesto en problemas de Minería de Textos, que involucran espacios de representación de muy alta dimensionalidad.

IV. REFERENCIAS

1. Schek, H. et al. “A quantitative analysis and performance study for similarity-search methods in high-dimensional spaces”, VLDB´98, New York, 1998, pp: 194-205.         [ Links ]

2. Ciaccia, P. et al. “M-tree: an efficient access method for similarity search in metric spaces”, VLDB´97, Atenas, 1997, pp: 426-435.         [ Links ]

3. Dickerson, M. “Algorithms for proximity problems in higher dimensions”, Computational geometry theory and applications, vol. 5, 1996, pp: 277-291.         [ Links ]

4. Bern, M. et al. “Probably good mesh generation”, J. Computer and Systems Science, vol. 48, 1994, pp: 384- 409.         [ Links ]

5. Nene, S. y Nayar, S. “A simple algorithm for nearest neighbour search in high dimensions”, IEEE Transactions on Pattern Analysis and Machine Intelligence”, vol. 19, num. 9, 1997, pp: 969-1003.         [ Links ]

6. Friedman, J. et al. “An algorithm for finding nearest neighbors”, IEEE Transactions on Computer, C-24, Oct 1975, pp: 1000-1006.         [ Links ]

7. Weber, R. y Blott, S. “An approximation based data structure for similarity search”, Technical report 24, ESPRIT project ERMES (no. 9141), 1997, pp: 1-25.         [ Links ]

8. Berchtold, S. et al. “Independent quantization: an index compression technique for high-dimensional data spaces”, ICDE´00, San Diego, USA, 2000, pp: 577-588.         [ Links ]

9. Yang, Y. y Pederson, J. “A comparative study on feature selection in text categorization”, ICML’97, Nashville, 1997, pp: 412-420.         [ Links ]

10. Ciesielski, K. et al. “Histogram-based dimensionality reduction of term vectors space”, CISIM’07, vol. 28, Artigas, F. et al. Cálculo de la vecinidad mediante grafos en minería de textos 170 num. 30, 2007, pp: 103-108.

11. Young-Sheng, C. et al. “Fast and versatile algorithm for nearest neighbor search based on a lower bound tree”, Pattern recognition letters, Elsevier, New York, vol. 40, num. 2, 2007, pp: 360-375.         [ Links ]

12. Gómez-Ballester, E. et al. “Some improvements in tree based nearest neighbour search algorithms”, CIARP’2003, Spring-Verlag, Berlin, 2003, pp: 456-463.         [ Links ]

13. Hjaltason, G. y Samet, H. “Ranking in spatial databases”, Symposium on Large Spatial Databases, Portlan, 1995, pp: 83-95.         [ Links ]

14. Seidl, T. y Kriegel, H. “Optimal multi-step k-nearest neighbor search”, SIGMOD´98, Seattle, Washington, USA, 1998, pp: 154-165.         [ Links ]

15. Pagel, B. et al. “Deflating the dimensionality curse using multiple fractal dimensions”, ICDE, San Diego, USA, 2000, pp: 589-598.         [ Links ]

16. Ciaccia, P. y Patella, M. “Pac nearest neighbour queries: approximate and controlled search in high-dimensional and metric spaces”, ICDE´00, Washington DC, 2000, pp: 244.         [ Links ]

17. M. R. K. y Shahabi, C. “Voronoi-based k nearest neighbor search for spatial network databases”, VLDB´2004, Toronto, 2004, pp: 840-851.         [ Links ]

18. Dasarathy, B. V. “Nearest Neighbor (NN) Norms: NN Pattern Classification Techniques”, Los Alamitos, California, IEEE Computer Society Press, 1991, 447 págs.         [ Links ]

19. Sebastiani, F. “Machine learning in automated text categorization”, ACM Computing Survey, vol. 34, num. 1, 2002, pp: 1-47.        [ Links ]