MODELADO Y SIMULACIÓN DEL MEDIDOR DE LA SENSACIÓN INSTANTANEA DE FLICKER DEL FLICKERMETRO DE LA NORMA IEC-61000-4-15 MEDIANTE REDES NEURONALES

Montoya Andrade, Dan El Andrés   Regoli, Carolina

El MSc. Dan El Andrés Montoya Andrade y la Ing. Carolina Regoli son Profesor Agregado y Profesora Instructora respectivamente en la Facultad de Ingeniería, Escuela de Ingeniería Eléctrica, Universidad Central de Venezuela, Ciudad Universitaria, Av. Los Estadios, Los Chaguaramos, Caracas, Fax 0212-6053105, teléfonos y correos electrónicos 0212-6053106, danelmontoya@gmail.com  y 0212-6053114, carolina.regoli@gmail.com  respectivamente.

Resumen:

La norma IEC-61000-4-15 plantea el diseño de un medidor de flicker de cinco etapas. Una primera etapa de adaptación de la señal, una segunda etapa de demodulación de la fluctuación de tensión, una tercera etapa de filtros ponderadores que simulan la respuesta en frecuencia a las fluctuaciones del sistema de visión humana, una cuarta etapa de premediación cuya salida representa la sensación instantánea de flicker, y una quinta etapa que realiza un análisis estadístico del nivel de flicker permitiendo el cálculo de parámetros de evaluación significativos (Pst y Plt). El objetivo del presente trabajo es modelar y simular hasta la cuarta etapa el flickermetro de la norma IEC-61000-4-15 mediante redes neuronales. Para esto se cuenta con un modelo de simulación del flickermetro realizado en Simulink desarrollado y probado según el estándar IEC-61000-4-15. Este modelo sirvió de referencia para efectos de validación y a través del mismo se obtuvieron los datos con los cuales se entrenó y probó la red neural. Mediante el estudio comparativo realizado se pudo concluir que el modelo neural representa satisfactoriamente al flickermetro de la norma IEC-61000-4-15.

Palabras clave: Flicker/ Red neuronal/ Sensación instantánea de flicker/ Flickermetro/ IEC-61000-4-15.

MODELATION AND SIMULATION OF THE FLICKER INSTANTANEOUS SENSATION TESTER OF THE IEC- 61000-4-15 STANDARD FLICKERMETER BASED ON NEURAL NETWORKS

Abstract:

The standard IEC-61000-4-15 present a five stages flickermeter design. A first one of signal adaptation, a second one that it demodulates and retrieveres of flicker voltage fluctuation, a third stage of filtered that it simulates the frequency respond of the human vision if this is excited by flicker fluctuations, a stage four of signal averaged with output signal the flicker instantaneous sensation, and a stage five that it makes an statistical analysis of the flicker level allowing the calculus of important parameters Pst and Plt. The object of this work is to model and to simulate a part of IEC-61000-4-15 flickermeter through neural network. For that we have a Simulink simulation model flickermeter developed and proved on IEC-61000- 4-15 standard. This model was used as reference to comparison and also it was used to generate the data to prove and validate the neural network model. Through of a comparative analysis it was concluded that the flickermeter neural network model represents satisfactorily the IEC-61000-4-15 flickermeter.

Keywords: Flicker/ Neural Network/ Flicker Instantaneous Sensation/ Flickermeter/ IEC-61000-4-15.

Manuscrito finalizado en Caracas, Venezuela el 2008/09/31, recibido el 2008/10/29, en su forma final (aceptado) el 2009/01/28.

I. INTRODUCCIÓN

La fluctuación en magnitud es la primera causa del efecto lumínico flicker. Para cuantificar el grado del voltaje flicker y facilitar la solución de los problemas relativos a él, se han propuesto varias definiciones y estándares [1]. Los estándares definen niveles de voltaje flicker permisibles en función de la frecuencia o índices de voltaje flicker, que es también expresado en función del voltaje flicker a varias frecuencias. Las redes neuronales, combinadas con el análisis ondícula de señales, se han usado ampliamente en la clasificación de las perturbaciones típicas en las mediciones de la calidad de potencia. Esto se observa en los trabajos de Santoso [2], Angrisani [3], Gaouda [4], Gaing [5], [6] y Lin [7]. En los trabajos de Lee [8] y Janik [9] se aplican las redes neuronales, conjuntamente con la Transformada S y las Máquinas de Soporte Vectorial, para clasificar eventos que afectan la calidad de potencia.

En el trabajo de Szlosek [10] se utilizó una red neuronal para la determinación de la sensación instantánea de flicker del flickermetro de la norma IEC-61000-4-15. En este trabajo se entrena una red neural con señales de variación de voltaje flicker senoidales de 20 Hz y amplitudes 0.15, 0.199, 0.35, 0.45 y 1 respectivamente. Para estas entradas se obtiene una red neural con precisión de 10-5 en 1500 iteraciones. El presente trabajo tiene como objetivo modelar y simular parte del flickermetro de la norma IEC-61000-4-15, mediante redes neuronales para todo el rango de frecuencias y amplitudes de variaciones de voltaje flicker senoidales, especificadas en el estándar IEC-61000-4-15. Específicamente se modelará la salida del bloque 4 o sensación instantánea de flicker de la norma antes mencionada. Para alcanzar el objetivo se utilizó un modelo de simulación del flickermetro, desarrollado y validado según la norma IEC- 61000-4-15 en la plataforma Simulink. A través de este modelo se generaron los datos de entrenamiento y prueba necesarios para el diseño de la red. Adicionalmente este modelo sirvió de referencia en la estimación de la eficiencia del medidor de flicker implementado a través de la red neural. Los resultados encontrados durante las pruebas permiten afirmar que se puede implementar mediante una red neural el flickermetro de la norma IEC-61000-4-15 de manera satisfactoria.

II. DESARROLLO

1. Marco Teórico

1.1. Redes Neuronales

Las redes neuronales son modelos computacionales que tratan de imitar la función de aprendizaje del cerebro. Están formadas por un conjunto de unidades de procesamiento llamadas “neuronas” conectadas en paralelo, que pueden filtrar y procesar las entradas para tomar decisiones. Una red neuronal se parece al cerebro en dos ideas básicas: La red necesita una cantidad de información para entrenarse y las conexiones entre las neuronas se usan para almacenar la información. El proceso utilizado para adaptar las conexiones o sinapsis se llama aprendizaje.

Para imitar las neuronas biológicas mediante neuronas artificiales se deben hacer algunas restricciones, llegándose a un modelo muy simplificado de neurona artificial que reproduce básicamente la actuación de las neuronas naturales. El uso de redes neuronales ofrece ventajas tales como el aprendizaje adaptativo, el procesamiento en paralelo en tiempo real, la tolerancia a fallas por la codificación redundante de la información y la capacidad autoorganizativa. El modelo de neurona artificial tiene cuatro elementos básicos: Un conjunto de sinapsis o enlaces caracterizados por un peso wi, un sumador que recibe las señales de las entradas xi de la neurona, las pondera por los respectivos pesos sinápticos y luego las suma, una función de activación o transferencia θ para limitar la amplitud de la salida de la neurona (existen varios tipos de funciones como la función escalón, la rampa y la sigmoidea) y una entrada b directa e independiente, que puede ser positiva o negativa. El modelo de la neurona descrito anteriormente se presenta en la ecuación 1 [13].

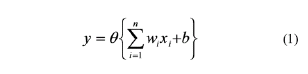
Existen muchos tipos de redes neuronales artificiales y cada una tiene su método de conectividad y a su vez su algoritmo de entrenamiento. Las más comunes son la red neuronal de una sola capa y la red neuronal de propagación multicapa. El entrenamiento de una red neuronal se asemeja a las técnicas de ajuste de curvas, donde las entradas y salidas de una función son conocidas pero la función en sí misma no lo es. El proceso de entrenamiento de una red neuronal consiste en encontrar los valores de los pesos sinápticos que conectan las entradas a la primera capa oculta, los pesos entre las capas ocultas y los pesos de la capa oculta previa a la capa de salida. Para esto debe calcularse el error de salida como la diferencia entre las salidas obtenidas a través de la red y las salidas deseadas. Una vez determinado el error de salida se propaga hacia atrás para encontrar los cambios adecuados en los pesos sinápticos de tal forma que se minimice el error de la salida. Este método de entrenamiento llamado retropropagación, minimiza el error mediante el algoritmo del máximo descenso que requiere del gradiente local en la capa de salida, respecto a los pesos sinápticos, el cual a su vez se propaga hacia la capa de entrada para tener un gradiente local para cada neurona en cada capa [13].

1.2 Flickermetro de la Norma IEC-61000-4-15

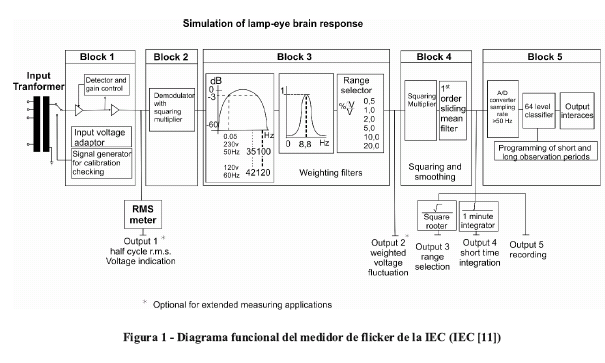
La norma IEC-61000-4-15 plantea el diseño de un medidor de flicker de cinco etapas. La primera etapa consta de un adaptador de tensión y un circuito para comprobación de calibración. La segunda etapa es un demodulador cuadrático recuperador de la fluctuación de tensión. La etapa 3 se compone de dos filtros dispuestos en cascada y un selector de margen. El primer filtro elimina las componentes de corriente continua y de rizado al doble de la frecuencia de salida del demodulador. El segundo filtro simula la respuesta en frecuencia a las fluctuaciones del sistema de visión humana. La etapa 4 está compuesta por un multiplicador cuadrático y un filtro pasabajo de primer orden. La salida de esta etapa representa la sensación instantánea de flicker. La etapa 5 realiza un análisis estadístico del nível de flicker permitiendo el cálculo de parámetros de evaluación significativos. En el diagrama de la Figura 1, al final del artículo, se presentan las diferentes etapas del flickermetro de la norma IEC-61000-4-15.

En el presente trabajo los autores proponen modelar y simular los bloques 3 y 4 del flickermetro mediante una red neuronal multicapa.

2. Metodología

El diseño de la red neuronal se realizó en Matlab tomando como datos de entrenamiento y prueba variaciones de voltaje flicker senoidales. Los datos de entrenamiento y prueba se obtuvieron del modelo de simulación realizado por Montoya [12] presentado en la Figura 2.

Este modelo fue desarrollado y simulado en el ambiente Matlab a través del Simulink y comprende los siguientes bloques generales recomendados en el estándar IEC-61000- 4-15:

• Bloque 1 adaptador de voltaje: En el estándar IEC-61000- 4-15 se especifica que debe escalarse el valor eficaz de la tensión de entrada a un nivel de referencia interno. De esta manera, pueden independizarse las medidas del flicker del nivel real de la tensión de entrada para así expresarlas en valores porcentuales.

• Bloque 2 demodulador cuadrático: El propósito de este bloque es recuperar la fluctuación de tensión elevando al cuadrado la tensión de entrada escalada, con el fin de simular el comportamiento de una lámpara. Este bloque se modela en el Simulink mediante una función cuadrática

• Bloque 3 filtros pasabajo, pasaalto y de ponderación: El bloque 3 está conformado por tres filtros, un retentor de orden cero y un amplificador. Los primeros dos filtros forman el filtro pasabanda que elimina la componente DC y la componente al doble de la frecuencia de alimentación. El primer filtro es pasaalto de primer orden con frecuencia de corte 0.05 Hz. El segundo filtro es Butterworth pasabajo de décimo orden con frecuencia de corte 42 Hz. El tercer filtro ponderador simula la respuesta en frecuencia a las fluctuaciones senoidales de tensión de una lámpara de gas (60 W - 120 V) con filamento enrollado en combinación con el sistema de visión humano. La función de transferencia del filtro de ponderación se presenta en la siguiente ecuación:

• Bloque 4 multiplicador cuadrático y filtro promediador: El propósito de elevar al cuadrado la señal flicker ponderada es la simulación del modelo de percepción visual no lineal del sistema ojo-cerebro. El filtro promediador se emplea para simular el efecto de almacenamiento en el cerebro. Este filtro es modelado con un filtro pasabajo de primer orden con constante de tiempo τ = 300ms. El último elemento del bloque 4 es un amplificador lineal que calibra la medición total a la salida del bloque. Como se ha comentado, la salida del bloque 4 es una medida de los cambios de voltaje ponderados por la sensibilidad del sistema lámpara-ojo-cerebro y representa la sensación instantánea de flicker.

• Bloque 5 analizador estadístico en línea de la señal flicker: El análisis estadístico comienza con el muestreo de la sensación instantánea de flicker a la frecuencia de 100 Hz. Luego se almacenan 60000 muestras que corresponden a un tiempo de 10 minutos. Con las muestras almacenadas se realiza un histograma de 64 clases que ayuda a construir la función distribución acumulativa de la permanencia de la señal flicker en cada una de las clases del histograma. Con ayuda de la función distribución acumulativa se calculan por interpolación lineal los percentiles alisados P0.1, P1, P3, P10 y P50 que son los niveles de flicker excedidos en el 0.1, 1, 3, 10 y 50% del tiempo de medición, respectivamente. Con estos percentiles se calcula el Pst o índice de severidad del flicker a corto plazo a través de la ecuación 3. El cálculo del histograma de la función distribución de probabilidades y del Pst se realizó con rutinas escritas en Matlab.

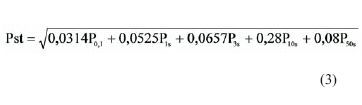
Basados en el modelo de simulación del flickermetro del trabajo de Montoya [12] se generaron para cientocincuenta (150) variaciones de tensión senoidales, especificadas a través de la frecuencia y la amplitud, cientocincuenta (150) valores de sensación instantánea de flicker. La frecuencia de la señal senoidal se varió entre 0.1 y 40 Hz y la amplitud entre 0.0005 y 0.2, obteniéndose sensaciones instantáneas de flicker entre 0.04 y 25. Debe comentarse que dentro de los valores de entrenamiento se encuentran los valores de prueba del flickermetro que recomienda la norma IEC-61000-4-15 para variaciones de voltaje flicker senoidales y sensación instantánea de flicker unitaria. Con estos valores se entrenó, mediante el algoritmo de retropropagación, una red neuronal con entradas la frecuencia y la amplitud de la señal variación de voltaje senoidal y con salida el valor de la sensación instantánea de flicker.

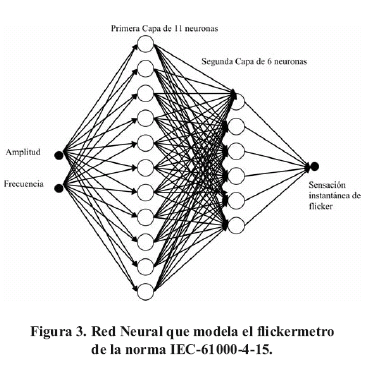
Partiendo del modelo de red neuronal de Szlosek [10], de tres (3) capas y doce (12) neuronas para la primera y segunda capa y una neurona para la tercera capa, se varió el número de capas y neuronas hasta obtener la red con mejor desempeño. La red que arrojó el menor error corresponde a una de tres (2) capas. La primera capa está formada por once (11) neuronas, la segunda capa está formada por seis (6) neuronas y la última capa por una (1) neurona. El entrenamiento de la red neuronal se detuvo en 25000 ciclos con un error de aproximadamente 10-4. La red neural se presenta en la Figura 3.

3. Resultados

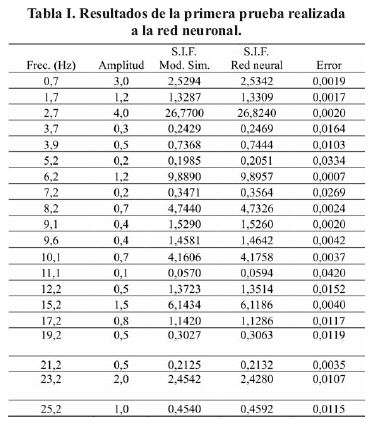
Las primeras veinte (20) pruebas realizadas a la red neuronal se presentan en la Tabla I. El error presentado es el relativo y se calculó mediante la diferencia de la sensación instantánea de flicker, calculada mediante el modelo de simulación, menos el valor obtenido de la red neuronal entre el valor arrojado por el modelo de simulación. Se puede observar que el error presente en las pruebas varía entre 0.17 % y 3.34 % obteniéndose un error promedio de 1.08%.

En una segunda fase de prueba se entrenó la red neuronal con 150 datos de entradas que incluían los valores de la Tabla 1. En este segundo examen a la red neuronal se obtuvo una variación del error entre 0.01 % y 15 % y un error promedio de aproximadamente 3 %.

4. Análisis de Resultados.

De los resultados obtenidos del proceso de entrenamiento y prueba de la red neuronal que simula los bloques 3 y 4 del flickermetro de la norma IEC-61000-4-15, se puede comentar lo siguiente: • Para variaciones de voltaje flicker senoidales, la sensación instantánea de flicker modelada y simulada con la red neuronal de retropropagación de tres (3) capas entrenada con veinte (20) datos, presenta un error promedio despreciable de 1.08% presentándose errores entre 0.17% y 3.34%. • Al aumentar el número de datos de entrenamiento ciento cincuenta (150) incluyendo las pruebas sugeridas en el estándar IEC-61000-4-15, el error promedio se ubicó entre 0.01% y 15% con un error promedio despreciable de 3%. • Debe entrenarse la red neuronal tanto con variaciones de voltaje flicker senoidales como rectangulares, dado que la norma IEC-61000-4-15 las exige en sus pruebas. • Estos resultados pueden tomarse como punto de partida para el modelado del último bloque del flickermetro de la norma IEC, es decir, podría diseñarse una red neuronal que modele en conjunto los bloques 3, 4 y 5 del dispositivo medidor de flicker.

III. CONCLUSIONES

Sobre la base de las pruebas realizadas al modelo de simulación neuronal del flickermetro de la norma IEC-61000- 4-15 en todo el rango de frecuencias y amplitudes de variaciones de voltaje flicker senoidales, especificadas en el estándar IEC-61000-4-15, incluyendo las pruebas que sugiere la norma, se puede concluir que la red neural con entradas la frecuencia y la amplitud de la variación del voltaje flicker, con tres capas con once (11), seis (6) y una (1) neurona respectivamente, y con salida la sensación instantánea de flicker, modela con un error despreciable el flickermetro del estándar IEC-61000-4-15.

IV. REFERENCIAS

1. Wierda R. Cuaderno Técnico Nro. 176. Flicker o parpadeo de las fuentes luminosas. Schneider Electric. 2001.         [ Links ]

2. Santoso S., et al. Power Quality Disturbance Waveform Recognition Using Wavelet-Based Neural Classifier - Part 1: Theoretical Foundation. IEEE Transactions on Power Delivery, Vol. 15, No. 1, January 2000, P. 222- 228.         [ Links ]

3. Angrisani L., Daponte P., D’Apuzzo M. Wavelet Network-Based Detection and Classification of Transients. IEEE Transactions on Instrumentation and Measurement, Vol. 50, No. 5, October 2001, P. 1425- 1435.         [ Links ]

4. Gaouda A, et al. Pattern Recognition Applications for Power System Disturbance Classification. IEEE Transactions on Power Delivery, Vol. 17, No. 3, July 2002, P.677-683.         [ Links ]

5. Gaing Z., Huang H. Wavelet-Based Neural Network for Power Disturbance Classification. Proceedings of IEEE Power Engineering Society Meeting, July 2003, P. 1621- 1628.         [ Links ]

6. Gaing Z. Wavelet-Based Neural Network for Power Disturbance Recognition and Classification. IEEE Transactions on Power Delivery, Vol. 19, No. 4, October 2004, P. 1560-1568.         [ Links ]

7. Lin C., Tsao M. Power Quality Detection with Classification Enhancible Wavelet-Probabilistic Network in a Power System Proceedings of Generation, IEE Transmission and Distribution Meeting, Vol. 152, No. 6,. November 2005, P.969-976.         [ Links ]

8. Lee I., Dash P. An S-Transform Based Neural Pattern Classifier for Non-Stationary Signals. Proceedings of IEEE International Conference on Signal Processing, August 2002, P. 1047-1050.         [ Links ]

9. Janik P., Lobos T. Automated Classification of Power- Quality Disturbances Using SVM and RBF Networks. IEEE Transactions on Power Delivery, Vol. 21, No. 3, July 2006, P. 1663-1669.         [ Links ]

10. Szlosek M., et al. Application of Neural Networks to Voltage Fluctuations Measurement - A Proposal for a New Flickermeter. Proceedings of 11th IEEE International Conference on Harmonics and Quality of Power, April 2004, P. 403-407.         [ Links ]

11. IEC. Norma Internacional. CEI IEC 61000-4-15. AENOR 1999.         [ Links ]

12. Montoya D. Realización del Flickermetro de la Norma IEC-61000-4-15 mediante la Transformada de Ondícula. Trabajo de ascenso a la categoría de Profesor Agregado, Escuela de Ingeniería Eléctrica, UCV. Junio 2006.         [ Links ]

13. Haykin S. Neural Networks, a Comprehensive Foundation. Prentice Hall. 2005.         [ Links ] Volumen 13, Nº 51, junio 2009. pp 137-142 142