Simulación mediante pspice de un modelo simplificado y de alta eficiencia de una batería de plomo - ácido

Fernández, Herman; Martínez, Abelardo; Guzmán, Víctor; Giménez, María.

El Dr. Herman Fernández es Profesor Titular en el Dpto. de Electrónica de la Universidad Nacional Experimental Politécnica “Antonio José de Sucre”, UNEXPO Vicerrectorado Puerto Ordaz, Telefax 0286-9621205, correo electrónico hermanfernand@gmail.com.

El Dr. Abelardo Martínez Iturbe es Profesor Titular en el Centro de Estudios Superiores de la Universidad de Zaragoza, España. Teléfono 34-976-761974, fax 34-976-762111, correo electrónico amiturbe@posta.unizar.es.

Los Dres. Víctor Guzmán Arguis y María Isabel Giménez son Profesores Titulares en el Dpto. de Electrónica y Circuitos, Universidad Simón Bolívar, Sartenejal, Baruta, Caracas, teléfono 0212-9063677, fax 0212-9063631, correos electrónicos vguzman@usb.ve. mgimenez@usb.ve respectivamente.

Resumen: Se presenta un nuevo modelo de una batería de plomo-ácido con un número reducido de elementos, menor tiempo de procesamiento, de alta eficiencia, con capacidad para admitir la parametrización de las resistencias de carga y descarga y de fácil adaptabilidad a otras herramientas de simulación. Para comprobar el funcionamiento del modelo se aplica una fuente externa que permite evaluar los modos de funcionamiento en carga y descarga. El ensayo de simulación demuestra una respuesta satisfactoria del modelo en los modos de carga y descarga, con una eficiencia que supera el 99%. Además se establecen comparaciones con otros modelos desarrollados, destacando sus ventajas y desventajas.            

Palabras clave: Baterías de plomo – ácido / Modelaje de baterías / Simulación de batería / Fuentes controladas / Bloques funcionales.

Pspice simulation of a simplified and highly efficient lead-acid battery model

Abstract: A new lead-acid battery model is presented, with a reduced component count, lower processing time, high efficiency, able to parametrize the charge and discharge resistances and easily adaptable to other simulation platforms. To prove the model, an external supply is used to evaluate the charge and discharge operating modes. The simulated test shows the satisfactory model response in the charge and discharge modes, with over 90% efficiency. Furthermore comparisons are made with other models, underlaying its advantages and disadvantages.

Keywords: Lead-acid batteries / Battery modeling / Battery simulation / Controlled sources / Function blocks.

Manuscrito finalizado en Puerto Ordaz, Venezuela el 2008/01/25, recibido el 2008/02/14, en su forma final (aceptado) el 2009/02/01.

I. INTRODUCCIÓN

Se ha reportado una gran variedad de modelos para representar los modos de funcionamiento de las baterías de plomo-ácido. Si bien es cierto que se ha conseguido producir modelos simplificados de baterías, basados en circuitos sencillos formados por resistencias, diodos y un condensador como elemento de almacenamiento [1]-[2], que pueden ser simulados en gran parte con las herramientas de simulación disponibles, dichos modelos requieren, por su misma topología, de una asignación directa de los parámetros comerciales de una batería: el voltaje en sus terminales y la capacidad de carga.

Ya se ha reportado un modelo de una batería basada en fuentes dependientes y bloques funcionales, que admite estos parámetros como variables de entrada al mismo [3]. Aunque los ensayos con este modelo demostraron un funcionamiento correcto en los distintos modos de operación, su estructura está formulada utilizando interruptores controlados por tensión, fuentes dependientes de voltaje y corriente, fuentes de corriente tipo espejo y una cantidad importante de objetos de tratamiento analógico (sumadores, restadores y elementos de retardo). Por otra parte, los valores de las resistencias de carga y descarga que utiliza el modelo deben ser calculados previamente a la puesta en marcha del programa, por no emplear el comando de asignación por vía de parámetros externos, lo cual resulta engorroso cuando se requiere examinar los efectos de los cambios en las resistencias en forma dinámica (paramétrica). La eficiencia alcanzada por este modelo fue menor al 85%, con un tiempo de corrida considerable y de difícil portabilidad a otras herramientas de simulación.

Para lograr obtener un modelo más eficiente, en este desarrollo se ha reducido el número de fuentes dependientes de voltaje gobernadas por tensión, y se han eliminado los interruptores controlados por voltaje y las fuentes tipo espejo de corriente. Con el fin de verificar la efectividad del modelo propuesto respecto a la primera versión, se realiza un ensayo de carga y descarga de la batería, en el que se demuestra su mayor eficiencia y un menor tiempo de procesamiento por parte de la herramienta de simulación.

En el presente trabajo se expone un resumen de las ecuaciones usadas para la simulación de una batería de plomo – ácido, se discute el modelo propuesto, se obtiene su respuesta en los modos de carga y descarga, se realizan las mediciones de la eficiencia de la batería y finalmente, se establecen las comparaciones con otros modelos y se exponen las conclusiones.

II. DESARROLLO

1. Ecuaciones del modelo de una batería de plomo-ácido

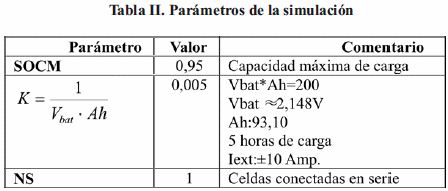
Con el análisis detallado de las ecuaciones que definen el modelo de las baterías de plomo-ácido realizado por Castañer [4], en la Tabla I se han resumido las ecuaciones que definen el voltaje y la resistencia durante los modos de carga y descarga.

2. Desarrollo del modelo

Una contribución de este trabajo es la propuesta de un esquema simplificado para el modelo de la batería que pueda ser usado por la mayoría de las herramientas de simulación capaces de admitir fuentes controladas y bloques matemáticos de operaciones fundamentales [5]. La Fig. 1 ilustra el modelo desarrollado, basado en los bloques de procesamiento analógicos disponibles en la librería del Pspice. El modelo propuesto puede ser usado directamente en la mayoría de los programas de simulación que utilizan fuentes controladas y bloques funcionales (PSpice, PSIM, PSCAD, etc.).

La fuente de intensidad I_ext se usa para comprobar el proceso de carga de la batería de acuerdo a los parámetros asignados como el voltaje de la batería, el número de celdas en serie, ns, la capacidad Ah y el estado de carga inicial, SOC1. Los elementos Dcarg, F2, Rcarga, Rcmeg, Ercarga y Ecarga representan el circuito de carga de la batería. El conjunto F2 – Rcarga – Ercarga modela la resistencia de carga R1. Debido a las restricciones del programa Pspice, que no permite asignar directamente variables calculadas en los nodos del circuito como parte de los parámetros del modelo de la resistencia disponible en la librería del Pspice, se ha representado la resistencia de carga con una topología formada por una fuente de corriente controlada por corriente, F2, actuando en configuración tipo “espejo de intensidad”, para producir un voltaje equivalente en la resistencia 1Ω, de magnitud igual al valor de corriente proveniente de la fuente externa conectada en la entrada del banco de baterías. La caída de voltaje en la resistencia se aplica como entrada a la fuente de voltaje controlada por voltaje, E_rcarga, que genera un voltaje de salida de acuerdo a la ecuación que determina la resistencia de carga de la batería. Los terminales de salida del módulo E_rcarga están conectados en serie con la fuente Ecarga. Este conjunto de partes (exceptuando la fuente E_carga) permite representar la resistencia de carga en función del valor del estado de carga calculado por el propio modelo, el número de celdas conectadas en serie y el estado de carga inicial; estos dos últimos parámetros debe ser asignados externamente al modelo mediante la instrucción “PARAMETERS”.

Es necesario incluir la resistencia R_cmeg para evitar el “error de flotación” que genera Pspice cuando detecta un nodo flotante respecto al terminal común del circuito. Cuado se detecta esta situación, la corrida del programa es abortada automáticamente.

El voltaje de carga interno de la batería se describe mediante la fuente dependiente Ecarga. El circuito de descarga de la batería se modela de manera similar, tomando en consideración la polaridad de la corriente de descarga que circula a través de Desc, cuando se aplica una fuente externa.

Es importante destacar que este modelo se basa en la existencia en Spice de las fuentes dependientes de voltaje controladas por voltaje, denominadas fuentes tipo “E” en el programa. El valor de la tesión de salida de estos elementos se define sobre la base de fórmulas que contienen valores constantes, variables provenientes calculadas en los nodos del circuito y parámetros externos asignados mediante el comando “PARAMETERS” del programa.

Esto permite definir el circuito para obtener el estado de carga de la batería, SOCN, a partir de la ecuación del estado de carga, tomando en cuenta el voltaje, Vbat, la corriente de la batería, Ibat y el estado inicial de carga, SOC1. El estado de carga del banco de baterías es calculado por los bloques aritméticos integradores (bloques de forma triangular) mostrados en la Fig. 1; el término del estado de carga en el instante anterior (t- t), es calculado por el bloque de procesamiento d/dt.

Para comprobar la respuesta del modelo se ha realizado un ensayo usando los datos reportados en la Tabla II y considerando que la celda es de 2,148V.

Para validar el funcionamiento del modelo se ha considerado un proceso de carga – descarga empleando una fuente de corriente bipolar en la entrada del circuito descrito en la Fig. 1.

3. Presentación y Discusión de Resultados

Para evaluar el proceso de carga, se aplica una fuente de corriente de +10A. Se ha asignado un valor inicial de estado de carga, SOC1=0,5. Los resultados obtenidos se ilustran en la Fig. 2a. En dicha figura se aprecia como la batería alcanza un estado de carga de 0,951 al transcurrir aproximadamente 5 horas. Este valor se corresponde con el valor de tiempo necesario para que la batería se cargue a 2,148V, tomando en cuenta el estado inicial del 50%. La energía transferida a la batería durante el proceso de carga es de 531,261Kwh. Cuando se somete la batería a un proceso de descarga, se toman nuevamente los valores al cumplirse 5 horas del proceso. Como se puede apreciar en la Fig. 2a, la batería se descarga nuevamente alcanzando un SOC1=0,5. La energía extraída de la batería es de 530,500Kwh.

La eficiencia calculada durante el proceso de carga-descarga simulado con el nuevo modelo ha sido del 99,85%, lo cual demuestra un comportamiento del modelo acorde con los valores asignados en el ensayo y con los resultados obtenidos en trabajos anteriores, donde la eficiencia conseguida varió entre el 90% [6] y cerca del 100% [7].

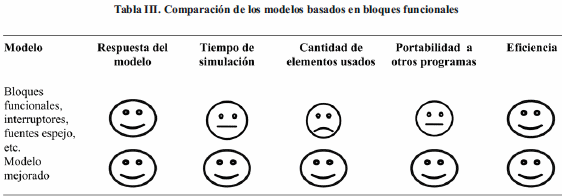
La Tabla III resume un estudio comparativo del modelo simplificado respecto a la primera versión. Ambos modelos funcionan adecuadamente, sin embargo, se aprecia que el modelo simplificado ofrece mejoras significativas respecto al modelo de bloques funcionales, en cuanto al tiempo de simulación, número de elementos y portabilidad a otros programas.

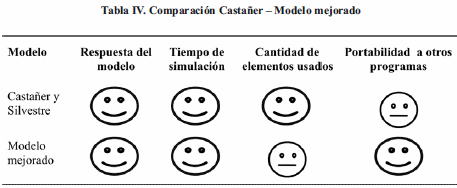
Comparándolo con el modelo desarrollado por Castañer (Tabla IV), el modelo simplificado es ahora aproximadamente igual en cuanto al número de partes. Sin embargo, el modelo propuesto en este trabajo se puede adaptar más fácilmente a otras herramientas computacionales que dispongan de bloques de procesamiento aritméticos.

El modelo desarrollado permite asignar los parámetros de capacidad de carga de la batería en Ah y del estado inicial de carga de la misma, necesarios para determinar el tiempo de respaldo que puede suministrar un banco de baterías cuando se usa como parte de un vehículo eléctrico, una fuente de alimentación ininterrumpida o un sistema fotovoltaico [8]- [10].

III. CONCLUSIONES

1. Usando los elementos disponibles en la librería “ABM” del Pspice, se ha podido representar una resistencia variable usando fuentes dependientes de voltaje y corriente.

2. Además de aceptar parámetros externos fijados por el usuario, cambia su magnitud de acuerdo al valor registrado en los nodos del circuito.

3. El modelo de la batería de plomo – ácido, trabaja satisfactoriamente.

4. Para la evaluación del modelo sólo se requieren asignar parámetros como la tensión de la celda, el valor Ah y el estado inicial de carga.

5. Este modelo permite demostrar la evolución de los estados de carga y descarga del banco cuando se aplica una fuente que obliga a conmutar entre dichos estados dinámicamente.

6. El modelo desarrollado permite asignar los parámetros de la capacidad de la batería en Ah y del estado inicial de carga del conjunto, necesarios para determinar el tiempo de respaldo que proporciona la energía disponible en la batería.

7. Este es uno de los elementos más importantes cuando se trata de modelar la operación global de sistemas complejos tales como cargadores de baterías, fuentes de alimentación ininterrumpida, sistemas fotovoltaicos, etc.

IV. REFERENCIAS

1. Salameh, Z., Cassacca, M., and Lynch W. “A Mathematical Model for Lead-Acid Batteries Determination of Lead-Acid Battery ”. IEEE Trans. On Energy Conversion, vol. 7, No. 1, March 1992, pp. 93-97.        [ Links ]

2. Casacca, M., and Salameh, Z. “Determination of Lead- Acid Battery Capacity Via Mathematical Modeling Techniques”. IEEE Trans. On Energy Conversion, vol. 7, No. 3, September 1992, pp. 442-446.        [ Links ]

3. Fernández, H., et. al. “Modelaje y simulación de una batería de plomo-ácido mediante fuentes dependientes de voltaje-corriente y bloques funcionales”. Universidad, Ciencia y Tecnología, Marzo 2005, Nº33, Vol.9, pp.35-41.        [ Links ]

4. Castaner. L. and Silvestre, S. 2002, “Modelling Photovoltaic Systems”. Wiley, London pp. 117-131.        [ Links ]

5. Fernández, H. Septiembre 2007, “Contribución al diseño de células de generación mixta eólica y fotovoltaica para ser usadas en emplazamientos aislados”. Tesis de doctorado en Ingeniería Electrónica. Universidad de Zaragoza. pp.48-55.        [ Links ]

6. Krim F. 2001, “A novel intelligent battery charge controller for stand-alone PV system”. EPE Conference, EPE, Gratz pp 1-9.        [ Links ]

7. Gergaud O, et al. 2003, “Energy modeling of a lead-acid battery within hybrid wind/photovoltaic systems”. EPE Conference, EPE, Toulouse  pp 1-10.        [ Links ]

8. García J. F., et al. 1997, “El vehículo eléctrico, tecnología, desarrollo y perspectivas de futuro”. Mc. Graw Hill, Madrid, pp.136-155.        [ Links ]

9. Gualda J. 1979, “Sistemas de alimentación ininterrumpida. “Electrónica y automática industriales”. Mundo electrónico. Barcelona, España,  pp.139-153.        [ Links ]

10. Gualda J.A., Martínez S., y Martínez P. 1992, “Electrónica industrial. Técnicas de potencia”. Alfaomega, Madrid, pp. 444-456.        [ Links ]