Universidad, Ciencia y Tecnología
versión impresa ISSN 1316-4821versión On-line ISSN 2542-3401
uct v.13 n.53 Puerto Ordaz dic. 2009
Identificación y validación del modelo no lineal de la temperatura del aceite superior de transformadores de potencia aplicando algoritmos genéticos.
Pérez, Rómulo Matos, Enrique Fernández, Sergio
El trabajo fue presentado en el IV Congreso Internacional de la IEEE ANDESCON 2008, realizado en la Ciudad de Cusco Peru durante los dias 15 al 17 de octubre de 2008.
El Dr. Romulo Perez es Profesor Asistente de la UNEXPO Vicerrectorado Barquisimeto, Tel/fax, 58-251-4423549, rperez@unexpo.edu.ve, romuloperez2003@gmail.com;
El Lic. Enrique Matos es Profesor de la Universidad de Cienfuegos Carlos Rafael Rodriguez, Facultad de Informatica, Cuba, gardero@gmail.com;
El Dr. Sergio Fernandez es Profesor Titular e Investigador del ISPJAE CIPEL, Av. 114-11901 Marianao, CP 19390, Cuba, Telef./fax 537-2663023, sfg@electrica.cujae.edu.cu.
Resumen:
Este trabajo presenta una técnica basada en Algoritmos Genéticos para la identificación y validación del modelo no lineal de la temperatura del aceite superior en los transformadores de potencia que está siendo utilizado en el sistema de monitoreo y diagnostico en línea instalado en un transformador de 100 MVA 230/115/24 kV OA/FA/FOA de la Subestación Barquisimeto de ENELBAR Venezuela desde el año 2003. Los resultados de la identificación por algoritmos genéticos se comparan con resultados obtenidos con identificación por mínimos cuadrados lineales y de las mediciones reales de la temperatura del aceite superior. Estos resultados además evidencian una reducción significativa del error en el modelo al realizar la identificación por algoritmos genéticos, lo cual mejora su desempeño como herramienta de diagnóstico para transformadores de potencia.
Palabras Clave:
Algoritmos Geneticos/ Transformadores de Potencia/ Identificacion/ DiagnosticoIdentification and validation of power transformers top oil temperature no lineal model by applying genetic algorithms.
Abstract:
This paper presents a technique based on Genetic Algorithms for the identification and validation of the top oil temperature no lineal model in power transformers used in on line diagnosis and monitoring systems, installed in a 100 MVA 230/115/24 kV OA/FA/FOA transformer of Substation Barquisimeto ENELBAR Venezuela since 2003. The results of the identification by genetic algorithms are compared with identification by least-squares and measured top oil temperature. The results demonstrate a significant reduction of the mistake in the model when making the identification by genetic algorithms, which improves its performance like as power transformer diagnosis tool.
Key words:
Genetic Algorithms/ Power Transformer/ Identification/ Diagnosis.Manuscrito finalizado en Barquisimeto, Edo. Lara, Venezuela, en el año 2008.
I. INTRODUCCIÓN.
Los transformadores de potencia son actualmente sometidos a estudios muy rigurosos para lograr su utilización en forma confiable y segura, dada la importancia que tienen en los sistemas electroenergéticos a nivel mundial. En años recientes, en los países más industrializados se han instalado sistemas de diagnóstico en tiempo real (SDTR) para transformadores, con la finalidad de conocer de forma instantánea el estado o condición y supervisar su funcionamiento en óptimas condiciones, de forma tal de lograr introducir un mantenimiento adecuado [1].
Uno de los componentes básicos de este tipo de sistema diagnóstico son los modelos térmicos, los cuales han tenido un amplio desarrollo de forma tal de mejorar la exactitud de sus resultados y de adaptarlos a las mediciones en tiempo real. En la solución de estos modelos a escala mundial se han utilizado diferentes técnicas y herramientas, y su desarrollo en forma general se puede sintetizar comenzando por los recomendados en la norma IEEE Std. C.57.91[2] e IEC-354[3], el anexo G de la norma IEEE Std. C.57.91-1995 propuesto por Pierce[4] y otros desarrollados en los últimos años por Lesieutre[5], Tylavsky[6], Swift[7]-[8], Lachman[9], Predhan[10], Tang [11] y Susa[12]-[14], entre otros.
La introducción y aplicabilidad de estos modelos está profundamente ligada a las características de los transformadores y a los transductores que componen los SDTR. Su desarrollo ha variado con el tiempo y en la actualidad se utilizan varios modelos en tiempo real cuyos resultados dependen casi directamente de los datos obtenidos en dichas instalaciones, de las técnicas empleadas para su tratamiento que permiten garantizar la identificación correcta de sus parámetros y de la experiencia en la interpretación de sus resultados. Por estas razones en los trabajos previos [15]-[19], los autores seleccionaron desde el año 1999, entre otros, el modelo para el cálculo de la temperatura del aceite superior propuesto por Lesieutre [5] también conocido como modelo del MIT (Instituto de Tecnología de Massachusetts) en su solución lineal, sobre el cual se han aplicado los métodos de estimación de parámetros por mínimos cuadrados y recientemente por Algoritmo Genético (AG) para el caso de la solución lineal [19].
Se han realizado diferentes estudios sobre las posibles fuentes de error de estos modelos [5, 20, 21, 22, 23] debido a los métodos utilizados en la estimación de sus parámetros y en lo relativo a la naturaleza, obtención y procesamiento de los datos, los cuales se han analizado diariamente durante más de 5 años con resultados similares a los anteriormente mencionados. Durante todo este tiempo los autores han experimentado con técnicas relacionadas con la calidad de los datos, como es el caso del tratamiento estadístico y el uso de filtros a partir de la transformada de Wavelet [18] con la finalidad de mejorar los resultados en identificación del modelo lineal (n = 1) teniendo como objetivo fundamental la disminución del error en los resultados.
Sin embargo consideraron propicio emplear el modelo no lineal para poder identificar el término n a partir de datos experimentales de campo con la aplicación de AG. Este es el objetivo fundamental que los autores ponen a consideración de los lectores y los resultados prácticos obtenidos en su aplicación. El desarrollo del trabajo presenta la estación experimental y tratamiento de los datos, el modelo matemático, la importancia de la identificación, breve análisis de los AG, AG para la estimación de parámetros y la metodología empleada para la identificación y validación del modelo térmico.
II. DESARROLLO.
1. Estación experimental y tratamiento de los datos.
En el ano 2003 se introdujo una instalacion en tiempo real en el transformador N° 2 de 100 MVA 230/115/24 kV OA/FA/FOA, de la subestacion Barquisimeto propiedad de la Energía Eléctrica de Barquisimeto ENELBAR en Venezuela [17] - [19], la cual aporta las variables necesarias que garantizan la aplicabilidad del modelo propuesto en línea y la de otros posibles modelos que están siendo incorporados al sistema de diagnóstico original. En la Fig. 1, se muestra el transformador seleccionado para su estudio.
El tiempo de muestreo escogido fue de 10 minutos. Las variables empleadas en el modelo son la corriente de carga, la temperatura ambiente y la temperatura del aceite superior, las cuales son registradas con equipos de adquisición de datos que garantizan el límite del error en ± 0,5 %. El rango de medición de las variables son de hasta 40 °C para la temperatura ambiente, hasta 150 °C para la temperatura del aceite superior y de 502 A para la corriente de carga. Una vez comenzado a registrar y almacenar dichas variables, las cuales son analizadas estadísticamente, se comprobó que en algunos casos se comportan erráticamente y se observaron problemas eventuales en la medición producto de factores ambientales, picos de corriente de carga y respuesta del instrumento de medición de la temperatura del aceite superior. Para corregir esta situación y poder acceder a datos experimentales confiables para la estimación de parámetros del modelo térmico, se aplicó un control de calidad y filtrado de datos, cuyos procedimientos se explican en detalle en [18].
2. Modelo Matemático
El grupo de investigación del MIT liderado por Lesieutre[5] propuso en el año 1997 un ingenioso modelo modificado para el cálculo de la temperatura del aceite superior donde consideran las variaciones continuas de la temperatura ambiente durante el ciclo de carga y que no son tenidas en cuenta en el modelo de la norma IEEE Std. C57.91 en su cláusula 7[2], en el cual la temperatura del aceite superior está dada por una ecuación diferencial de primer orden:
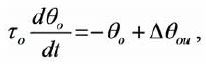 (1)
(1)
donde:
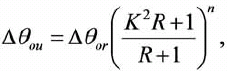 (2)
(2)
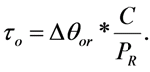 (3)
(3)
De esta manera, la temperatura del aceite superior esta dado por:
![]() (4)
(4)
Este modelo fundamental tiene la limitacion de que no es aplicable en sistemas de monitoreo en linea (on-line) [5].
El modelo modificado del MIT propone:
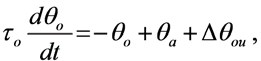 (5)
(5)
de la cual se obtiene:
 (6)
(6)
donde:
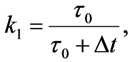 (7)
(7)
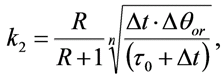 (8)
(8)
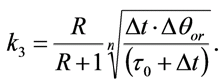 (9)
(9)
2.1. Importancia de la Identificación.
Para realizar una adecuada modelación de la temperatura del aceite superior, se necesita que el modelo físico descrito anteriormente sea ajustado al transformador específico que se analiza. Esto implica la obtención de los parámetros o identificación del modelo anteriormente mencionado. De no ser así, sería imposible obtener una buena predicción del modelo para fines de diagnostico, debido a que los errores previstos deben ser de baja cuantía (menor a 2 °C) [5, 10, 11, 24].
Este proceso se hace a partir de las mediciones experimentales en tiempo real obtenidas de la instalación experimental inicialmente mencionada, con las cuales se puede aplicar diversos métodos de cálculo que contemplen ecuaciones no lineales, ya que las magnitudes involucradas son independientes.
Con el objetivo de determinar los exponentes involucrados en los modelos no lineales se necesita un método de optimización capaz de contemplar este tipo de ecuaciones.
En este trabajo se presenta un enfoque basado en Algoritmos Geneticos, una tecnica de la inteligencia artificial que puede ser usada en la optimizacion de ecuaciones, sin depender de su naturaleza.
2.2.Breve Análisis de Algoritmos Genéticos (AG).
Los Algoritmos Genéticos (AG) son una técnica de la Inteligencia Artificial donde los problemas a resolver son enfocados desde un punto de vista análogo a la teoría de la evolución genética [26, 27, 28]. Los AG resuelven problemas clásicos de optimización de ecuaciones:
![]() (10)
(10)
donde:
D = Espacio de busquedaHaciendo pequenas transformaciones en la funcion, se puede analogamente maximizar el valor de
f(x) .Las posibles soluciones x al problema planteado son representadas como un vector (o cromosoma) de componentes (o genes), que contienen la información de la solución. Entre ellas se definen procedimientos de selección, cruzamiento (encargados de mezclar, de forma aleatoria, partes de la información que tienen dos individuos) y mutación (encargados de cambiar aleatoriamente la información perteneciente a un individuo) [27].
Los individuos son seleccionados por un proceso análogo a la selección natural, que basado en el criterio que se persigue (min. ó máx. f(x) ) y también en cierta aleatoriedad, escoge los más fuertes; para con ellos realizar cruzamientos y mutaciones explorando el espacio de búsqueda D y de esta manera encontrar la mejor solución al problema [27, 28].
Cada paso del proceso define una población (conjunto de j soluciones posibles) en la cual se conservan las z (generalmente z = 1) mejores soluciones de la población anterior. Este proceso es llamado Elitismo [28], importante en los algoritmos genéticos, ya que garantiza la convergencia de estos a medida que aumenta el número de iteraciones. En la tabla I se describe el procedimiento utilizado para la implementación de un algoritmo genético.
Se define además un criterio adicional de parada para el proceso descrito, que puede estar en función de un valor lo suficientemente bueno de f(x), una cantidad máxima de generaciones o generaciones sin mejoras en la solución, o incluso en función del tiempo demorado o tiempo demorado sin mejoras en la solución. Al final del proceso se escoge el mejor de los individuos. La convergencia al óptimo global está demostrada cuando los algoritmos genéticos utilizan el proceso de elitismo [28].
2.3. Algoritmos Genéticos para la estimación de parámetros.
La estimación de parámetros k1, k2, k3, kx de una ecuación f(x) se puede definir como un problema de optimización donde la función de optimización (FO) será el mínimo error cuadrático medio (ECM) de la diferencia entre los valores reales yi (valores obtenidos mediante mediciones experimentales) y los valores estimados utilizando los valores de los parámetros en f(x) o sea:
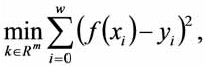 (11)
(11)
donde se supone que se tiene un conjunto de entrenamiento (xi , yi) en el cual se encuentran los w datos a emplear en la estimación de los parámetros. Un individuo es un vector k (de m componentes) de los parámetros de la función f(x). Para ese vector de valores reales, se pueden definir las operaciones de mutacion y cruzamiento lo que permite que el AG pueda explorar el espacio de soluciones del problema.
Para resolver (6), la ecuacion no lineal (n ≠ 1), se necesitan identificar: k1, k2, k3 y n. Como funcion de optimizacion en el AG se utiliza:
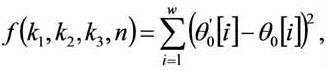 (12)
(12)
donde
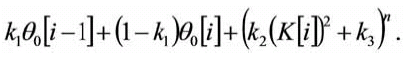 (13)
(13)
Esta ecuacion evalua la exactitud de los parametros del modelo, para un conjunto de entrenamiento formado por mediciones experimentales de las magnitudes
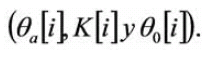 (13.1)
(13.1)
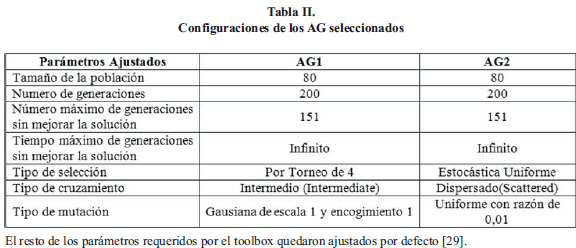
Para la identificación del modelo se empleo el programa Matlab® y su toolbox de algoritmos genéticos [29]. Se implementaron dos algoritmos genéticos con diferentes técnicas de selección, cruzamiento y mutación denominados AG1 y AG2. Sus ajustes fueron seleccionados en función de resultados previos obtenidos de múltiples configuraciones, para así escoger de entre ellas las dos mejores. En la tabla 2 se muestran sus ajustes.
2.4. Metodología para la identificación y validación del modelo térmico.
Los datos seleccionados para realizar el estudio fueron las semanas 1, 2 y 3 del mes de Abril de 2008.
Los conjuntos de entrenamiento (CE) son formados por las semanas 1 y 2 de forma independiente.
El conjunto de datos donde se evalúan los parámetros encontrados del modelo a partir del de entrenamiento, se denomina conjunto de validación (CV). El conjunto de validación de la semana 1 es la semana 2. El conjunto de validación de la semana 2 es la semana 3.
Se realizan 10 corridas de cada uno de los AG (AG1y AG2), se calcula el promedio para evitar los efectos estocásticos de estos algoritmos y se presenta la mejor solución particular.
Se realiza la identificación del modelo por mínimos cuadrados (MC) empleando el software Gret1 [30] para efectos comparativos.
Los criterios matemáticos empleados para evaluar los resultados de la estimación de parámetros son:
Raiz del error medio cuadratico (REMC); dado por la expresion:
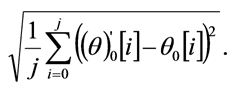 (14)
(14)
Media de los valores absolutos de los errores (ME) evaluados en todos los puntos; esta dado por la expresion:
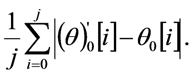 (15)
(15)
Error Maximo (EMax) evaluado en todos los puntos; esta dado por la expresion:
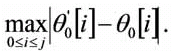 (16)
(16)
3. RESULTADOS
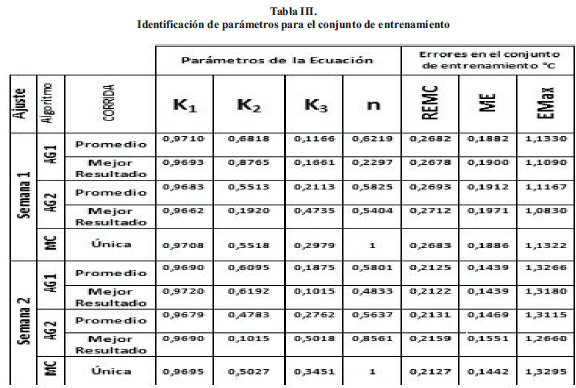
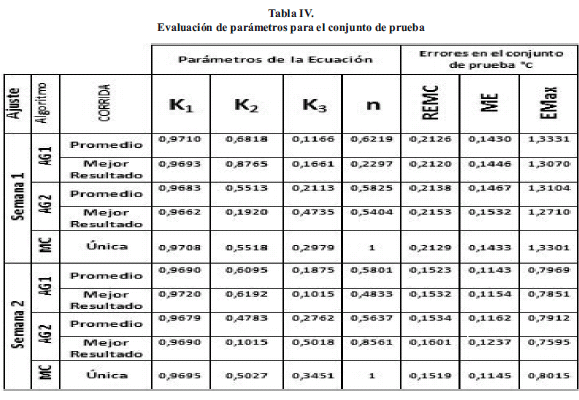
A continuacion se presenta los resultados en las Tablas III y IV correspondientes a la identificacion y evaluacion de parametros para los conjuntos de entrenamiento y validacion.
4. ANÁLISIS DE RESULTADOS
Conjunto de Entrenamiento (CE)
Al comparar los valores de los errores descritos en la Tabla III correspondiente a la identificación de parámetros para el conjunto de entrenamiento en la semana 1, se observa que la temperatura del aceite superior estimada con AG2 en su promedio es más exacta que la estimada con AG1 y MC. El error máximo del mejor resultado de la estimación AG2 es de 1,08 °C, el del AG1 es de 1,10 °C y el del MC es de 1,13 °C, lo que resulta en una mejora del AG2 en la reducción del EMax del 4,42 % con respecto al MC.
En la semana 2, se observa que la temperatura del aceite superior estimada con AG2 en su promedio es más exacta que la identificada con AG1 y MC. El error máximo del mejor resultado de la estimación AG2 es de 1,26 °C, el del AG1 es de 1,31 °C y el del MC es de 1,33 °C, lo que resulta en una mejora en la reducción del EMax del 5,26 % con respecto al MC.
Conjunto de Prueba (CV)
Al comparar los valores de los errores descritos en la Tabla IV correspondientes a la evaluación de parámetros para el conjunto de prueba de la semana 1, se observa que la temperatura del aceite superior estimada con AG2 en su promedio es más exacta que la estimada con AG1 y MC. El error máximo del mejor resultado de la estimación AG2 es de 1,27 °C, el del AG1 es de 1,30 °C y el del MC es de 1,33 °C, lo que resulta en una mejora en la reducción del EMax del 4,51 % con respecto al MC.
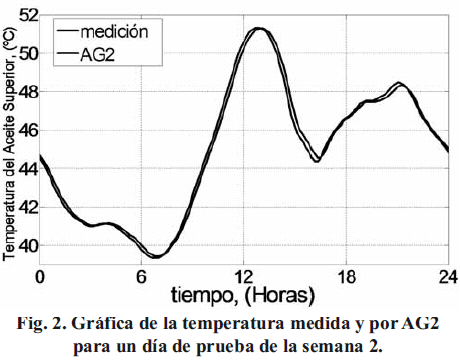
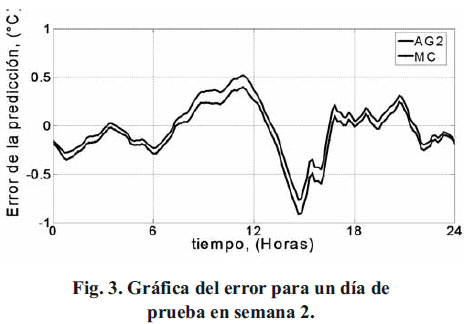
En cuanto al conjunto de prueba de la semana 2, se observa que la temperatura del aceite superior estimada con AG2 en su promedio es más exacta que la estimada con AG1 y MC. El error máximo del mejor resultado de la estimación AG2 es de 0,76 °C, el del AG1 es de 0,78 °C y el del MC es de 0,80 °C, lo que resulta en una mejora en la reducción del EMax del 5 % con respecto al MC. En la Fig. 2 se muestra la grafica ampliada de la temperatura del aceite superior real medida y la resultante con AG2, para un día de prueba de la semana 2.
A continuacion, en la Fig. 3 se muestra la grafica del error para el dia anteriormente graficado entre el AG2 y el MC
Finalmente se puede evidenciar a partir de los resultados mostrados en la Tabla IV que el modelo no lineal estimado a partir del Algoritmo Genético AG2 tiene un mejor desempeño que el modelo estimado a partir de los mínimos cuadrados para la predicción de la temperatura del aceite superior en transformadores de potencia.
Símbolos y Acrónimos
θ
o Temperatura del aceite superior, °C.θ
a Temperatura ambiente, °C.θ
ou Ultima temperatura del aceite superior, °C.Δθ
o Aumento de la temperatura del aceite superior sobre la temperatura ambiente, °C.Δθ
or Aumento de la temperatura del aceite superior sobre la temperatura ambiente a carga nominal. °C.Δθ
oi Aumento de la temperatura inicial del aceite superior para t = 0, °C.Δθ
ou Ultimo aumento de temperatura del aceite superior, °C.n Exponente empirico usado para calcular la variacion de
Δθo con los cambios en la corriente de carga y generalmente dado en funcion del sistema de enfriamiento.Δ
t Intervalo de tiempo, h.to Constante de tiempo del aceite, h.
K
Relacion de corriente de carga / a corriente nominal.R Relacion entre perdidas con carga nominal y sin carga.
C Capacidad termica del transformador (W-h/°C).
PR
Perdidas totales en W a carga nominal.Ir Corriente de carga nominal, A.
5. CONCLUSIONES
1) Se ha evidenciado que el uso de los algoritmos genéticos en sus dos variantes AG1 y AG2, para la identificación de parámetros del modelo de la temperatura del aceite superior en su solución no lineal, tiene un mejor desempeño que la estimación de parámetros por mínimos cuadrados, que se refleja en un menor EMax al compararlo con los valores experimentales medidos y donde además las REMC y EM se encuentran en valores muy cercanos al obtenido por MC.
2) Se observa que en línea general el algoritmo AG2, tiene un mejor comportamiento promedio que el AG1, motivado al uso de diferentes tipos de cruzamiento, mutación y selección que el AG1.
3) Se evidencia resultados más exactos dado a que se estima el valor del parámetro n, lo que mejora la predicción de la temperatura del aceite superior para diferentes niveles de temperatura ambiente, corriente de carga y sistema de enfriamiento al cual es sometido el transformador en su ciclo de carga diario.
4) Se recomienda el uso del modelo no lineal debido a que los transformadores no siempre operan en condiciones de n=1, como es el caso bajo estudio.
5) Conociendo entonces que los algoritmos genéticos permiten la identificación de parámetros de los modelos, sin importar cuán complicados estos sean, se sugiere el desarrollo de trabajos futuros en la identificación de otros modelos desarrollados para la predicción de la temperatura del aceite superior.
6) Finalmente, se puede observar que ambas técnicas (AG y MC) son excelentes para la predicción de la temperatura del aceite superior, donde se evidencia un bajo error máximo que está muy por debajo de los 2 °C empleados por diferentes autores [5],[10],[11],[24].e instituciones internacionales para la validación de sus resultados de modelación térmica.
AGRADECIMIENTOS
Los autores expresan su reconocimiento a la Empresa Energía Eléctrica de Barquisimeto ENELBAR y a la Universidad Nacional Experimental Politécnica Antonio José de Sucre UNEXPO en Venezuela, por facilitar el financiamiento y la instalación de la estación experimental de diagnostico de grandes transformadores en la Subestación Barquisimeto, lo que garantizó recabar los datos necesarios desde hace 5 años para llevar adelante este y futuros trabajos de investigación.
6. REFERENCIAS
1. FERNÁNDEZ, S., DIAGNÓSTICO, TÁCTICA Y ESTRATEGIA. REVISTA INGENIERÍA ENERGÉTICA, VOL. XX, N° 4, JUL. 1999, PP. 47-53. [ Links ]
2. IEEE, Guide for Loading Mineral-Oil-Immersed Transformers, Standard C57.91-1995, 1995. [ Links ]
3. IEC, Loading Guide for Oil Inmersed Power Transformers, IEC-354. 1991, 1991. [ Links ]
4. Pierce, L., Predicting Liquid Filled Transformer Loading Capability. IEEE Transactions on Industry Applications, Vol. 30, N° 1, Ene./Feb. 1994, pp. 170- 178. [ Links ]
5. Lesieutre, B., Hagman, W. y Kirtley, J., An Improved Transformer Top Oil Temperature Model for Use in An On-Line Monitoring and Diagnostic System. IEEE Transactions on Power Delivery, Vol. 12, N° 1, Ene. 1997, pp. 249-256. [ Links ]
6. Tylavsky, D., He, Q., Si, J. y McCulla, G., Transformer Top-Oil Temperature Modeling and Simulation. IEEE Transactions on Industry Applications, Vol. 36, N° 5, Sep./Oct. 2000, pp. 1219-1225. [ Links ]
7. Swift, G., Molinski, T. y Lehn, W., A Fundamental Approach to Transformer Thermal Modeling. Part I. IEEE Transactions on Power Delivery, Vol. 16, N° 2, Abr. 2001, pp. 171-175. [ Links ]
8. Swift, G., Molinski, T., Bray, R. y Menzies, R., A Fundamental Approach to Transformer Thermal Modeling. Part II. IEEE Transactions on Power Delivery, Vol. 16, N° 2, Abr. 2001, pp. 176-180. [ Links ]
9. Lachman, M., Griffin, P., Walter, W. y Wilson, A., Real- Time Dynamic Loading and Thermal Diagnostic of Power Transformers. IEEE Transactions on Power Delivery, Vol. 18, N° 1, Ene. 2003, pp. 142-148. [ Links ]
10. Pradhan, M. y Ramu, T., Prediction of Hottest Spot Temperature (HST) in Power and Station Transformers. IEEE Transactions on Power Delivery, Vol. 18, N° 4, Oct. 2003, pp. 1275-1283. [ Links ]
11. Tang, W., Wu, H. y Richardson, Z., A Simplified Transformer Thermal Model Based on Thermal-Electric Analogy. IEEE Transactions on Power Delivery, Vol. 19, N° 3, Jul. 2004, pp. 1112-1119. [ Links ]
12. Susa, D., Matti, L. y Hasse, N., Dynamic Thermal Modelling of Power Transformers. IEEE Transactions on Power Delivery, Vol. 20, N° 1, Ene. 2005, pp. 197- 204. [ Links ]
13. Susa, D. y Matti, L., Dynamic Thermal Modelling of Power Transformers - Further Development :part I. IEEE Transactions on Power Delivery, Vol. 21, N° 4, Oct. 2006, pp. 1961-1970. [ Links ]
14. Susa, D. y Matti, L., Dynamic Thermal Modelling of Power Transformers: further Development-part II. IEEE Transactions on Power Delivery, Vol. 21, N° 4, Oct. 2006, pp. 1971-1980. [ Links ]
15. Ramírez, O., Modelación físico-matemática para el diagnóstico de grandes transformadores en tiempo real. Tesis doctoral dirigida por Sergio Fernández Centro de Investigaciones y Pruebas Electroenergéticas CIPELISPJAE. CUBA, 2001. [ Links ]
16. Pérez, R., Fernández, S., Ramírez, O., Modernos métodos de diagnóstico aplicados a grandes transformadores en tiempo real. Revista Edelca, Año XXV, N° 4, 2002, pp. 22-23. [ Links ]
17. Pérez, R., Fernández, S., Ramírez, O., Sistema de Diagnostico de Transformadores de Potencia a Distancia. Revista Universidad Ciencia y Tecnología, Volumen 10, Nº 41, Dic. 2006, pp. 269-275. [ Links ]
18. Pérez, R., Fernández, Y., Matos, E., Fernández, S., Procesamiento de Datos Mediante Wavelet para la Modelación Térmica de Grandes Transformadores. Articulo actualmente arbitrado para su publicación en la Revista Técnica de la Universidad del Zulia. Venezuela, May. 2009. [ Links ]
19. Pérez, R., Matos, E., Fernández, S., Estimación de Parámetros y Validación del Modelo Lineal de la Temperatura del Aceite Superior en Transformadores de Potencia Aplicando Algoritmos Genéticos. Articulo actualmente arbitrado para su publicación en la Revista Técnica de la Universidad del Zulia. Venezuela, May 2009. [ Links ]
20. Tylavsky, D., Mao, X. y McCulla, G., Transformer Thermal Modeling: Improving Reliability Using Data Quality Control. IEEE Transactions on Power Delivery, Vol. 21, N° 3, Jul. 2006, pp. 1357-1366. [ Links ]
21. Morris, A., Comparing Parameter Estimation Techniques for an Electrical Power Transformer Oil Temperature Prediction Model. Langley Research Center NASA, Tech Rep. TM-1999-208974, Ene. 1999. [ Links ]
22. Jauregui-Rivera, L., Tylavsky, D., Acceptability of Four Transformer Top-Oil Thermal ModelsPart I: Defining Metrics. IEEE Transactions on Power Delivery, Vol. 23, N° 2, Abr. 2008, pp. 860-865. [ Links ]
23. Jauregui-Rivera, L., Tylavsky, D., Acceptability of Four Transformer Top-Oil Thermal ModelsPart II: Comparing Metrics. IEEE Transactions on Power Delivery, Vol. 23, N° 2, Abr. 2008, pp. 866-872. [ Links ]
24. Vilaithong, S. Tenbohlen, T. Stirl, Improved Top Oil Temperatute model for Unsteady-State Conditions of Power Transformers. Proceedings of the XIVth International Symposium on High Voltage Engineering, China (2005) F-42, Disponible en www.unistuttgart.de/ieh/forschung/veroeffentlichungen/2005_ish_rummiya.pdf. [ Links ]
25. Vilaithong, R., Tenbohlen, S. y Stirl, T., Investigation of Different Top-oil Temperature Models for On-line Monitoring System of Power Transformer.. Institute of Power Transmission and High Voltage Technology, University of Stuttgart, Tech. Rep. 2006. Disponible en www.unistuttgart.de/ieh/forschung. [ Links ]
26. Holland, J., Adaptation in Natural and Artificial Systems. Ann Harbor, University of Michigan Press, 1975. [ Links ]
27. Gen, M y Cheng, R., Genetic Algorithms and Engineering Optimization. New York, Wiley-IEEE, 2000. [ Links ]
28. Coello, C., Introducción a la Computación Evolutiva. Ediciones CINVESTAV-IPN. Instituto Politécnico Nacional, México, May. 2003. [ Links ]
29. Matlab®. The Language of Technical Computing. Toolbox Genetic Algorithm. Version 7.2.0.232, (2006). [ Links ]
30. Software Gnu Regression, Econometrics and Timeseries Library. Gret1 (2009). [ Links ]












 uBio
uBio