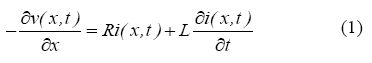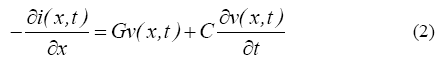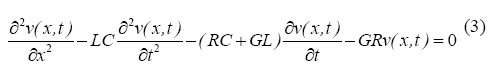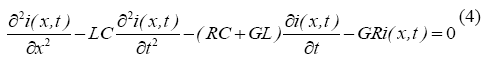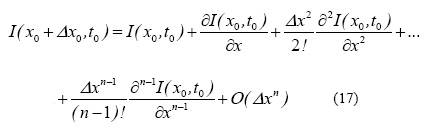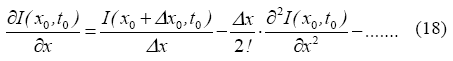Modelación de la onda del rayo a través de las ecuaciones del telegrafista

Requena Durlym¹, Contreras Ely¹, Roque Juan¹

1 UNEXPO, Vicerrectorado Puerto Ordaz, Venezuela, Dpto. de Ingeniería Mecánica Email: drequena@poz.unexpo.edu.ve

Resumen:

Este artículo describe un modelo de onda de impacto del rayo utilizando las ecuaciones diferenciales del telegrafista y su solución numérica a través del método de los elementos finitos. A través de un algoritmo de simulación y utilizando los recursos del MatLab, se describe el comportamiento en el tiempo y el espacio del efecto transitorio de la onda del rayo en condiciones ideales y con pérdidas. Se reproduce una onda doble-exponencial de Heidler para ilustrar aplicabilidad y validación del método propuesto.

Palabras clave: Onda del Rayo/ Ecuación del Telegrafista/ Elementos Finitos/ Discretización.

Recibido Marzo 2013, Aceptado Junio 2013

I. INTRODUCCIÓN

Las tormentas eléctricas y los rayos constituyen un matrimonio casi indisoluble, y con toda certeza donde exista actividad atmosférica con nubes altamente cargadas existirán los rayos. Los procesos eléctricos e intercambios de cargas que se desarrollan en el interior de las tormentas están íntimamente relacionados con la dinámica o movimiento de la nube y la microfísica de esta [1], [2]. Las ondas de corriente producidas por la descarga de un rayo, pueden producir altos niveles de tensión en tiempos muy cortos por el orden de los microsegundos y pueden causar daños permanentes en el aislamiento interno no regenerativo y cebados en el aislamiento externo del sistema eléctrico causando las salidas forzadas de este.

Durante muchos años, se han realizado una gran cantidad de estudios sobre este tema. Algunos se han preocupado sólo en la recolección de estadísticas, algunos en la toma de mediciones [3], [4] y otros han tratado de sondear más profundamente la naturaleza física del fenómeno del rayo.

El estudio y el cálculo numérico de la propagación de una onda de corriente o de tensión tipo rayo sobre una línea de transmisión como resultado de los impactos directos e indirectos sobre esta, revisten gran importancia por cuanto permiten el diseño seguro y económico del aislamiento, así como la selección de los dispositivos de protección adecuados para mitigar el efecto de estas.

El cálculo de los campos eléctricos y electromagnéticos radiados por un rayo, requieren del desarrollo de modelos que especifiquen el pulso de corriente en función del tiempo y del espacio en todos los puntos a lo largo del canal del rayo radiado, tal como lo investiga [5]. Estos campos pueden ser utilizados como elementos de entrada para el estudio de los modelos de acoplamiento electromagnético, los cuales son muy importantes en el estudio de las tensiones inducidas [6], [7] y en la determinación de los parámetros eléctricos de una línea eléctrica.

La onda electromagnética producida por un rayo, puede ser analizada a través del modelo de ondas viajeras en una línea de transmisión, tal como ha sido referenciado por los autores [8], [9], [10]. Si suponemos la nube cargada y la superficie de la tierra como dos placas que forman un gran condensador, y suponemos una alta intensidad de campo eléctrico a punto de producir una descarga disruptiva entre ambas placas, podemos decir que el canal de descarga dentro de la nube de tormenta estará completamente desarrollado formando un cortocircuito en el momento de producirse la descarga del líder y el subsecuente impacto de retorno. La propagación de la onda electromagnética a lo largo de la ruta de acceso puede ser tratado como un problema de circuito, donde la tensión V(x, t) y corriente i(x, t) se expresan en función de la variable espacial x y la variable temporal t.

En teoría, las características de propagación de una onda de corriente tipo rayo sobre una línea de transmisión puede ser descrita matemáticamente en forma de ecuaciones diferenciales en derivadas parciales a través de las ecuaciones de Oliver Heaviside basado en las ecuaciones del Telegrafista referenciado en los trabajos realizados por los autores [10], [11], [12], las cuales permiten ser resueltas pasando de una ecuación diferencial a una ecuación algebraica, y describen el comportamiento de una onda viajera en el tiempo y el espacio para el análisis de transitorio de la tensión y la corriente sobre una línea de transmisión.

Los problemas en ecuaciones diferenciales en derivadas parciales que hacen escena en los fenómenos físicos, se suelen clasificar en tres tipos principales: problemas parabólicos, elípticos e hiperbólicos, siendo estos últimos utilizados para estudiar fenómenos oscilatorios, vibraciones de cuerdas, membranas y oscilaciones electromagnéticas, cuya principal característica es la velocidad infinita de propagación de la perturbación, la cual corresponde a nuestro estudio.

En el caso de las líneas sin pérdidas cuando se desprecia la resistencia y la conductancia en derivación que representan las pérdidas de aislamiento, las ecuaciones del sistema pueden ser simplificadas en forma de la ecuación de onda para representar una onda viajera tipo rayo que se propaga a lo largo de la línea sin ningún tipo de atenuación. Aunque las ecuaciones diferenciales en derivadas parciales hiperbólicas de onda tienen ecuaciones exactas, en algunos casos pueden aparecer discontinuidades sobre la línea de transmisión, las cuales producen pérdidas y problemas de reflexiones que puede aumentar la complejidad y no linealidad de las ecuaciones del sistema.

En este trabajo hemos utilizado el método de las diferencias finitas como una herramienta para hallar la solución numérica de la ecuación del telegrafista, el cual aplica en modelos matemáticos de sistemas continuos.

Esta publicación ha sido organizada en seis secciones separadas. En la Sección II se presenta un desarrollo breve del modelo matemático de una línea de transmisión como modelo para el estudio de propagación de la onda del rayo, así como la formulación de la forma de onda doble-exponencial de Heidler. La Sección III describe el método de discretización y de elementos finitos empleado en la aplicación del estudio de propagación de la onda del rayo en una línea de transmisión. La Sección IV describe el algoritmo de simulación empleado y las condiciones de estabilidad aplicadas. La Sección V se presenta la discusión y análisis de los resultados obtenidos. La Sección VI corresponde al apartado de las conclusiones.

II.- DESARROLLO

1. Modelo de onda sobre una línea de transmisión.

1.1. Modelación matemática

Las líneas de transmisión son utilizadas en muy diversas áreas de la ingeniería eléctrica, desde el transporte de grandes bloques de energía en alta tensión, como canal de transmisión de datos, voz, transmisión de señales de protección y hasta la recepción de señales satelitales. Si bien es muy diverso el tipo de líneas que se utiliza para cubrir cada necesidad específica, todas ellas responden a los mismos principios básicos de funcionamiento descritos a través de las denominadas "Ecuaciones del Telegrafista" que dan las expresiones de las tensiones y corrientes a lo largo de la línea, en función del tiempo y el espacio.

Oliver Heaviside desarrolló un modelo matemático de línea de transmisión, que describe la variación instantánea de la tensión y corriente eléctricas a lo largo de un conductor. La teoría fue desarrollada para las líneas de transmisión de comunicaciones, como los hilos telegráficos y los conductores de radiofrecuencia; sin embargo, también es aplicable en su totalidad al diseño de las líneas de transmisión de potencia.

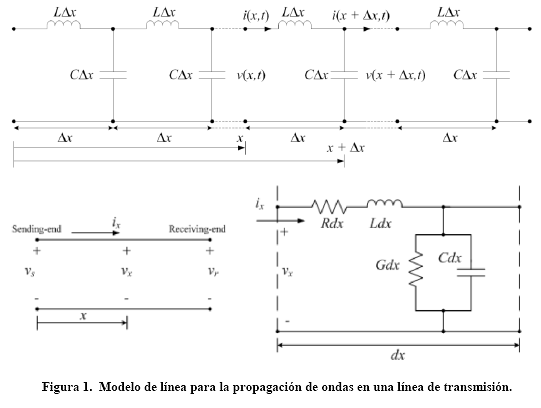
La Figura. 1 muestra la estructura y el circuito equivalente de una pequeña sección de una línea de transmisión eléctrica monofásica, el cual también ha sido utilizado por los autores [10], [11] y [12].

Si suponemos que los conductores de línea son paralelos al suelo y distribuido de manera uniforme, las características de dominio de tiempo en forma de ecuaciones diferenciales parciales de la línea se pueden expresar de la siguiente manera.

Derivando la ecuación (1) respecto de "X" y la ecuación (2) respecto de "t", con ayuda de manipulación algebraica y combinando ambas, se obtiene un par de ecuaciones diferenciales parciales hiperbólicas de una sola incógnita, las cuales se muestran.

Donde:

I(x, t) es la función de onda de la corriente transitoria.

V(x, t) es la función de onda de la tensión transitoria.

La inductancia "L" modela el proceso de almacenamiento energético en forma de campo magnético que se produce en la línea, se expresa en Henrios por unidad de longitud (H/longitud). La capacitancia "C" modela el proceso de almacenamiento energético en forma de campo eléctrico que se produce en la línea, y se expresa en Faradios por unidad de longitud (f/Longitud). La resistencia "R" modela la disipación de potencia debido a la no idealidad de los conductores (pérdidas óhmicas) y la conductancia "G" modela la disipación de potencia que se produce por la no idealidad del medio dieléctrico (pérdidas dieléctricas).

Según ecuaciones diferenciales (3) y (4), la descripción de los fenómenos que se presentan en una línea, se expresan convenientemente por medio de los valores que adoptan la tensión "v" y la corriente "i", cuyos valores varían punto a punto a lo largo de la línea y son funciones del tiempo y del espacio, es así que tenemos expresiones del tipo u(x, t) e i(x,t). De esta manera el comportamiento de la línea puede conocerse resolviendo las expresiones que vinculan a ambas expresiones.

Cuando los parámetros R y G son muy pequeños, sus efectos se pueden ignorar, y la línea de transmisión se puede considerar ideal y sin pérdidas. En este caso, el modelo depende sólo de los parámetros L y C, de los cuales obtenemos un par de ecuaciones diferenciales parciales, una de ellas para la tensión y otra para la corriente, ambas en función de la posición o distancia "X" y del tiempo "t".

Consideremos la ecuación de onda (3). Para que el planteamiento del problema esté completo, es necesario especificar las condiciones de contorno y las condiciones iniciales. La tensión v(x, t) en el suelo se supone que es cero, mientras que la corriente i(x, t) en la nube se supone que es de un valor pequeño y constante el cual puede ser considerado también como cero. Por lo tanto, las condiciones de contorno son:

Donde h es la altura de la nube o canal del rayo.

Para t = 0, se asume que la distribución de la tensión es un valor constante conocido, excepto en el suelo donde tiene el valor de cero. Por lo tanto, la condición inicial es:

1.2. Formulación de la forma de onda del rayo.

Los estudios de las ondas de corriente tipo rayo con altos valores de cresta, provienen de los trabajos realizados por Berger’s [3¡Error! Marcador no definido.], [4], [13]. Según los investigadores, la onda del primer impacto de retorno tiende a elevarse de manera gradual hasta la cresta en contraste con las ondas de los subsiguientes impactos. El frente de onda de los impactos subsecuentes, tienen la capacidad de crear tensiones superiores sobre los apoyos de las líneas de transmisión. Sin embargo, la cola que tiende a caer rápidamente y ayuda a remediar cualquier tensión que se desarrolle.

Todas las formas de onda del rayo presentan una característica básicamente cóncava, pero no existe un modelo único. En esta sección se presenta la forma típica para representar el rayo, la cual es a través de una función doble exponencial (9) desarrollada por Heidler [14], la cual es ampliamente utilizada para modelar el comportamiento de los transitorios de frente rápido cuando un rayo impacta sobre una línea de transmisión.

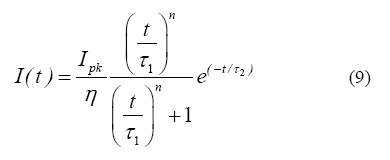
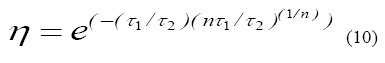
Ipk Valor de cresta de la corriente

t₁  Constante de tiempo de subida

t₂ Constante de tiempo de cola

n Factor de concavidad (Usualmente n = 5)

h Factor de corrección del valor de cresta

El factor de corrección del valor de cresta de la función de Heidler, es válida sólo para factores de concavidad n > 3.

La naturaleza aleatoria del rayo hace que la magnitud de la corriente (Ipk) inyectada por este y las constantes del tiempo de subida y bajada (t₁ y t₂) no sean las mismas en cada descarga [15]. Si esta onda de corriente es inyectada sobre una línea de transmisión, tomando en consideración variables como la impedancia características de los apoyos (Z_t), características del aislamiento, puesta a tierra y otros elementos importantes involucrados en el desempeño transitorio de la descarga, la onda de corriente implicará la generación de ondas de tensión también expresadas en forma de una doble exponencial experimentando la atenuación correspondiente y las subsecuentes reflexiones durante su viaje.

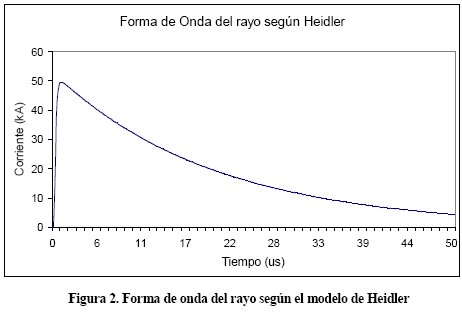
En la actualidad, los parámetros que definen la forma de onda del rayo, es a través del tiempo del frente t_f, el cual es 1.6 veces el tiempo para pasar del 30 % al 90 % del máximo valor de cresta, y el tiempo de cola t_t, el cual corresponde al tiempo para alcanzar el 50 % del máximo valor de cresta ya alcanzado. La Fig. 2 muestra la forma de onda de corriente del rayo de Heidler, para un tiempo de barrido de 0 – 50 μs. Los valores de los parámetros de ploteo que la describen son los siguientes: η = 0.9566, n = 5, t₁ = 0.5 μs, t₂ = 20 μs, t_f = 1.2 μs, t_t = 15 μs .

La ecuación (9) satisface dos requerimientos básicos necesarios para la simulación del rayo, los cuales consisten en que la corriente no debe tener discontinuidades en t = 0 s, así como la primera derivada de la corriente respecto al tiempo (dI/dt).

2. Modelación numérica y metodo de discretización.

La idea principal del cálculo con diferencias finitas, es reemplazar las derivadas parciales con combinaciones lineales de valores de funciones discretas. Las diferencias finitas tienen la virtud de simplificar y pueden ser utilizadas para representar una gran proporción de los métodos numéricos empleados en diferentes aplicaciones de la física. El método consiste en discretizar primero el problema dominante, de manera que las variables dependientes exhiban puntos discretos y para luego aproximar las derivadas con diferencias finitas, lo que resulta en una representación algebraica de la ecuación diferencial parcial [16]. La naturaleza de la ecuación resultante dependerá del carácter y complejidad del problema.

Si consideramos la ecuación (4) para representar la variable dependiente "I" en un dominio bidimensional representado por las coordenadas (x,t), la función continua I(x,t) puede ser sustituida por la función I(iΔx, jΔt) Los puntos pueden ser situados de acuerdo a las coordenadas de los valores de (i, j), realizando las siguientes sustituciones:

Aplicando la definición de derivada para la función I(x₀,t₀) tenemos que:

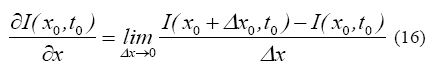
Si I(x,t) es continua, la ecuación (17) será una aproximación razonable de   para un Δx₀ finito lo suficientemente pequeño.

El desarrollo de la aproximación diferencial se realiza a través de una serie de Taylor [17], [18] expandiendo la función I(x_o+ Δx_o, t_o).

El desarrollo de la aproximación diferencial se realiza a través de una serie de Taylor [19], [20] expandiendo la función I(x_o+ Δx_o, t_o).

Resolviendo la ecuación (17) se obtiene la diferencia hacia delante, la cual es de la forma:

Si realizamos las sustituciones de las ecuaciones (11) y (15) en la expresión (18), obtenemos:

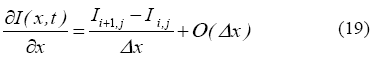
De manera similar se obtiene la diferencia hacia atrás.

La segunda derivada es aproximada como: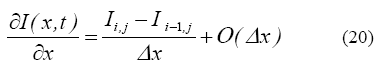

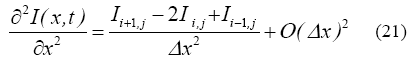
De manera similar, las derivadas en función de "t" pueden ser resueltas, resultando una representación 2D, obteniéndose una imagen de la ecuación de cinco puntos de la expresión de Laplace en 2D, donde:

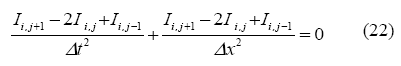
Con una truncación de o(Δx)²  + o(Δt)²

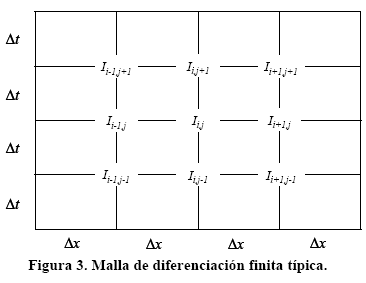
El desarrollo expuesto tiene como propósito resolver sistemas diferenciales continuos, en sistemas discretos a través de aproximaciones finitas, lo cual se logra mediante la creación de un número finito de puntos que dividen cada eje en pasos de diferenciación [17],[18]. La malla para el caso estudiado se muestra en la Figura. 3.

Consideremos la ecuación (4) y realicemos las sustituciones correspondientes, resulta una expresión algebraica de la forma:

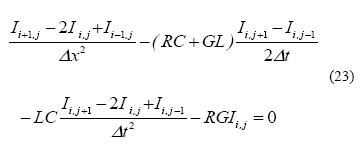
Luego, según la malla de diferenciación finita de la Figura. 3 y a objeto de obtener un término futuro en el tiempo de discretización, se procede a despejar el término

I_i,j , resultando la expresión (24), la cual es resuelta a través de elementos finitos mediante simulación.

3. Simulación y condiciones de estabilidad

3.1. Algoritmo de simulación.

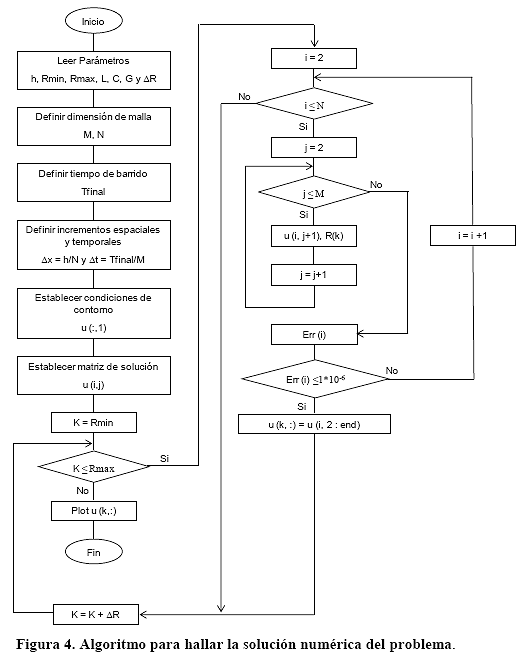
Para hallar la solución numérica de la ecuación (24), se ha procedido a la elaboración de un algoritmo que ha sido implementado en código MatLab, el cual se muestra en la Figura 4.

En este caso es importante tomar en cuenta las siguientes consideraciones.

◊ Definir e introducir los parámetros eléctricos de la línea que reproducirán las características del canal del rayo, tales como la altura (h) de la nube, la resistencia del canal (R_min y R_max), la inductancia (L), la capacitancia (C), la conductancia (G).

◊ Para proceder a discretizar, es necesario definir las dimensiones de la malla (N, M).

◊ Definir el tiempo de barrido de la gráfica de salida de discretización (T_final).

◊ Definir los incrementos espaciales ( ) y los incrementos temporales ( ) establecidos durante el proceso de discretización en la malla de diferenciación finita. Conocido los incrementos espaciales y temporales, es posible determinar el número de nodos mínimo que darán la solución del problema.

◊ Establecer las condiciones de contorno y las condiciones iniciales apropiadas para la solución del problema.

◊ Establecer una malla de solución que permita disponer la solución gráfica de problema.

3.2. Condiciones de estabilidad.

La estabilidad de un sistema totalmente discreto, se logra escogiendo espacios de tiempo que satisfagan la condición CFL (Counrant Friedrich Levy). En matemáticas, la condición CFL es un estado de convergencia de las ecuaciones diferenciales en derivadas parciales solucionadas a través de algoritmos y el método de las diferencias finitas. En este caso, el paso de tiempo debe ser inferior a un valor característico, de lo contrario la simulación podría producir resultados incorrectos e inestabilidad.

Por ejemplo, si una onda está cruzando una malla de diferenciación finita, entonces el intervalo de tiempo debe ser inferior que el tiempo necesario para que la onda atraviese los puntos de la malla adyacente. Cuando la separación entre los puntos de la malla se reduce, el límite superior para el intervalo de tiempo es inferior.

El número de Counrant (C) se expresa como sigue:

El valor de "C" puede cambiar de acuerdo con el método utilizado para resolver la ecuación de discretización. Si la solución es explícita, el valor máximo de C es 1 (C_max ≤ 1). Si la solución es implícita, esta es menos sensible a la inestabilidad numérica, de manera que valores de C mayores de 1 pueden ser tolerados.

Para garantizar la estabilidad del proceso se debe cumplir la siguiente condición donde Δx es la longitud del elemento espacial.

4. Discusión de resultados.

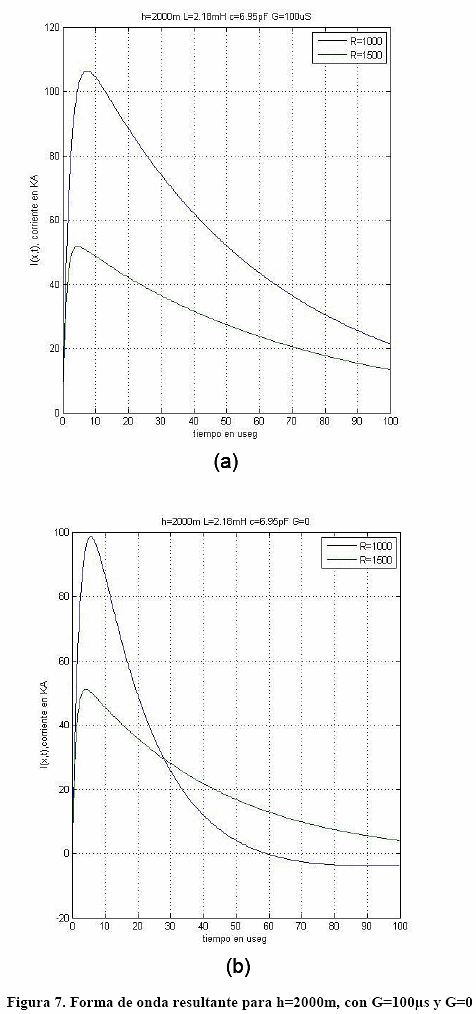
En el problema se han considerado alturas (h) del canal del rayo de 1000, 1500 y 2000 m los cuales son valores típicos, la inductancia (L) se le ha asignado un valor de 2.18 mH, mientras que a la capacitancia (C) un valor de 6.95 pF, conductancia (G) de 100μs y resistencia (R) en magnitudes de 1000 Ω y 1500 Ω.

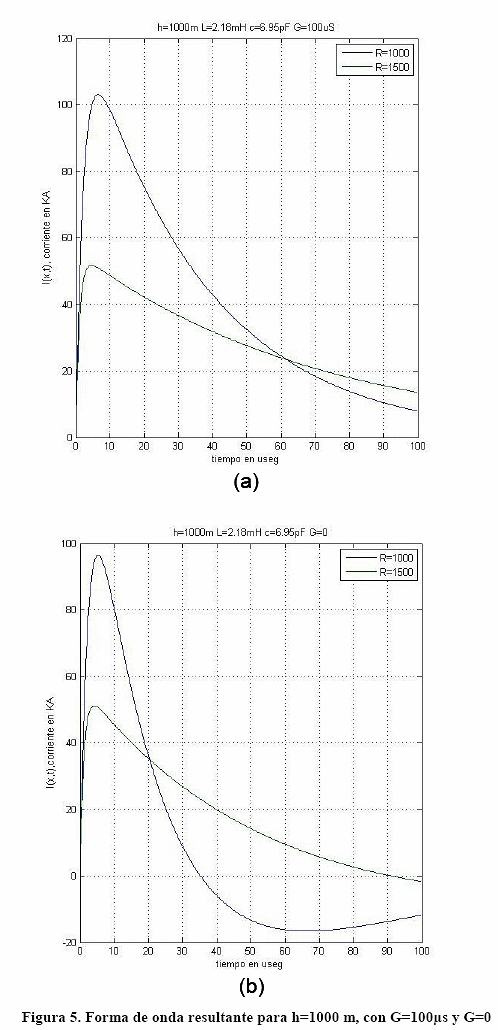
La simulación ha sido realizada valuando dos casos particulares, el primero considerando el circuito modelo con pérdidas (G ≠ 0), el segundo en condiciones ideales y sin pérdidas (G = 0). Las Fig. 5, 6 y 7, muestran las formas de ondas de la corriente del rayo obtenidas en la simulación, las cuales han sido realizadas con los parámetros indicados.

Las formas de ondas de la Figura. 5 obtenidas a través del código MatLab, corresponden al caso para una altura (h) del canal del rayo 1000 m, conductancia (G) 100 μS y 0 μS, así como resistencia de 1000 Ω y 1500 Ω, manteniendo inalterables el resto de los parámetros según los valores ya declarados. Según las ondas registradas en ambos escenarios de la Figura. 5, observamos a primera vista el efecto de atenuación introducido por la resistencia R y la conductancia G. Se aprecia en la Fig. 5a, que para un valor de resistencia de 1000 Ω, el valor de cresta de la onda del rayo alcanza aproximadamente los 104 kA, mientras que para los 1500 Ω la misma consigue alcanzar los 54 kA. También se observa un efecto de atenuación en el tiempo de cola "t_f", se puede apreciar que para un valor de resistencia de 1000 Ω, el tiempo de cola es aproximadamente 34 μs, mientras que para 1500 Ω, el mismo es de unos 42 μs, lo cual otorga una mayor residencia de energía del rayo, aun que con un menor valor de cresta.

También se aprecia efecto de atenuación introducido por la conductancia G, por ejemplo, para el caso de una línea ideal y sin pérdidas (G = 0), los valores de cresta alcanzados son mayores en contraste con el caso de conductancia de 100 μS. También se aprecia una disminución del tiempo de cola "t_f" para ambos casos.

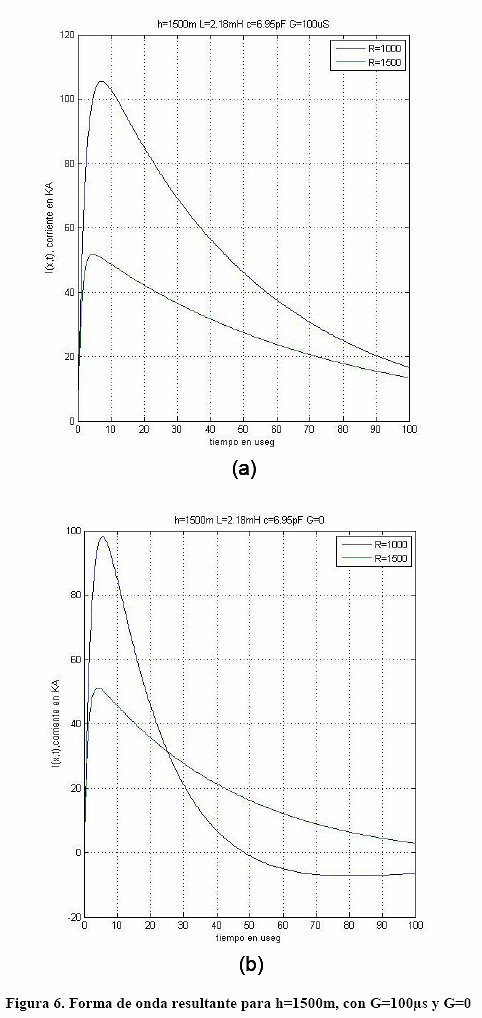
Al contrastar el efecto de la altura del canal del rayo en las Figuras. 5, 6 y 7, lo primero que se observa es un ligero incremento del valor de cresta de la corriente del rayo a medida que la altura también incrementa.

El fenómeno se puede observar tanto para el caso de conductancia 100 μS y 0 μS. No obstante, el mayor efecto observado es, a medida que incrementa la altura también incrementa el tiempo de viaje, lo cual se evidencia al examinar incremento del tiempo de cola para todos los casos analizados.

III. CONCLUSIONES

1. En este trabajo se ha presentado la ecuación del telegrafista para modelar la forma de onda de un rayo.

2. Se ha demostrado que la aplicación de las ecuaciones diferenciales parciales y su solución numérica a través del método de los elementos finitos es viable para reproducir el comportamiento de onda viajera del rayo en contraste con los métodos clásicos utilizados por otros investigadores.

3. Se modeló una onda del rayo a través de las expresiones de Heidler, la cual contrasta con los resultados obtenidos.

IV. REFERENCIAS

1. Richard E. Orville, Lightning Phenomenology, State University of New York at Albany, The National Academy of Sciences, 2000.        [ Links ]

2. E. Philip Krider, Physics of Lightning, University of Arizona, The National Academy of Sciences, 2000.

3. R. B. Anderson, A. J Eriksson "Lightning Parameters for Engineering Application", ELECTRA N° 69, 1980, Study Commitee n° 33 (Overvoltages and Insulation Co-ordination), CIGRE.

4. Lightning and Insulator Subcommittee of the T&D Committee, Parameters of Lightning Strokes: A Review, IEEE Transactions on Power Delivery, Vol. 20, N° 1, January 2005.

5. Celio Fonseca Barbosa and José Osvaldo Saldanha Paulino. "A Time-Domain Formula for the Horizontal Electric Field at the Earth Surface in the Vicinity of Lightning". IEEE TRANSACTIONS ON ELECTROMAGNETIC COMPATIBILITY, VOL. 52, NO. 3, AUGUST 2010. p.640.

6. P. Chowdhuri. "Electromagnetic Transients in Power Systems". Research Studies Press Ltd, John Wiley & Sons Inc, Copyright 1996.

7. Alexandre Piantini, and Jorge M. Janiszewski. Lightning-Induced Voltages on Overhead. Lines—Application of the Extended Rusck Model. IEEE TRANSACTIONS ON ELECTROMAGNETIC COMPATIBILITY, VOL. 51, NO. 3, AUGUST 2009.

8. Chang-Chou Hwang. "Numerical Modeling of Lightning Based on the Traveling Wave Equations". IEEE TRANSACTIONS ON MAGNETICS, VOL. 33, NO. 2, 1520 MARCH 1997.

9. Kokiat Aodsup and Thanatchai Kulworawanichpong. "Simulation of Lightning Surge Propagation in Transmission Lines Using the FDTD Method". World Academy of Science, Engineering and Technology 71 2012.

10. G. Hariharan, R. Rajaraman, K. Kannan. "Haar wavelets approach of traveling wave equation-A plausible solution of lightning stroke model". International Journal of Engineering and Technology, 2 (2) (2013) 149-156.

11. C. F. Chen and C. H. Hsiao, "Haar wavelet method for solving Inmped and distributed-parameter systems". IEE Proc. -Control Theory Appl. Vol. 144, no 1, January 1997.

12. I.T. Chiang and S.K. Jeng. "A Haar Wavelet Approach for Solving the Transient Response of Inhomogeneous Transmission Lines" Antennas and Propagation Society International Symposium, 2000. IEEE Volume: 4 Page(s): 2183 - 2186 vol.4.

13. IEEE Working Group Report, "Estimating Lightning Performance of Transmission Lines II- Updates to Analytical Models". IEEE Transactions on Power Delivery, Vol 8, N° 3, July 1993.

14. F. Heidler, J.M.CvetiC and. V. Stanic. "Calculation of Lightning Current Parameters". IEEE Transactions on Power Delivery, Vol. 14, No. 2, April 1999, p. 399.

15. William A. Chisholm, John G. Anderson, Reviewer: Mat Darveniza. Chapter 6: Lightning and Grounding. EPRI AC Transmission Line Reference Book—200 kV and Above, Third Edition. Final Report, December 2005.

16. Enrique Zuazua. "Métodos Numéricos de resolución de Ecuaciones en Derivadas Parciales". Basque Center for Applied Mathematics (BCAM), Bilbao, Spain, zuazua@bcamath.org. http://www.bcamath.org/zuazua/. January 2009.

17. José Antonio Ezquerro Fernández. "Iniciación a los Métodos Numéricos", Capítulo 6: Resolución numérica de los problemas de valor inicial. Iberus, Universidad de la Riojas, Servicio de publicaciones, 2012, p.62.

18. D. M Causon. ―Introductory Finite Difference Methods for PDEs. 2010 Professor C.G Mingham &Ventus Publishing ApS. ISBN 978-87-7681-642-1. (Ec Dif Parci y Serie Taylor).

19. Zulma Millán, Leonor de La Torre, Laura Oliva, María del Carmen Berenguer. "SIMULACIÓN NUMÉRICA. ECUACIÓN DE DIFUSIÓN". Revista Iberoamericana de Ingeniería Mecánica. Vol. 15, N.º 2, pp. 29-38, 2011.

20. Juan David Jaramillo Jaramillo, Antonio M. Vidal Maciá, Francisco José Correa Zabala. Métodos Directos para la Solución de Sistemas de Ecuaciones Lineales Simétricos, Indefinidos, Dispersos y de gran Dimensión. UNIVERSIDAD EAFIT, Medellin, Febrero De 2006. Documento 40-022006.