Universidad, Ciencia y Tecnología
versión impresa ISSN 1316-4821
uct vol.20 no.78 Puerto Ordaz mar. 2016
Modelo para la estimación de las pérdidas de propagación en redes WLAN operando en 2,4 ghz y 5,8 ghz, para ambientes interiores de edificios comerciales
Juan M. Torres1, Ángel Pinto-Mangones1, Mario R. Macea A.2, Nelson A. Pérez-García3 y Leidy Marian Rujano3
1 Escuela de Ingeniería de Sistemas, Universidad del Sinú, Montería, Colombia. 2 Escuela de Ingeniería de Sistemas, Universidad de Córdoba, Montería, Colombia. 3 Grupo de Investigación de Telecomunicaciones, Universidad de Los Andes, Mérida, Venezuela.
Resumen: El prácticamente indetenible despliegue de redes WLAN a nivel mundial, tanto en ambientes interiores como exteriores, exige el desarrollo de estrategias, modelos, métodos y técnicas que incremente la precisión en el proceso de planificación y dimensionamiento de las mismas, en uno de sus principales segmentos como lo es el de radio propagación, estrechamente relacionado con la estimación de la cobertura, con el fin de disminuir la probabilidad de sub-dimensionamiento o sobredimensionamiento de dichos sistemas. Por ello, en este artículo se desarrolla un modelo semi-empírico para la predicción de pérdidas de propagación en ambientes interiores, utilizando mediciones de la potencia recibida, realizadas en dos edificios comerciales de la ciudad de Guayaquil, Ecuador. El nuevo modelo incluye la atenuación sufrida por la señal al atravesar pisos y paredes, un factor de pérdidas dependiente de la altura del transmisor y además considera un exponente de pérdidas de potencia también relacionado con dicha altura. El modelo desarrollado es comparado con otros modelos existentes en la literatura, en términos de la raíz del error medio cuadrático o RMSE, observándose un mejor desempeño de dicho modelo en los todos los escenarios de medición considerados.
Palabras Claves: Redes WLAN, pérdidas de propagación, ambientes interiores, modelo semi-empírico.
Path loss predictionmodel for WLAN operating at 2.4 ghz and 5.8 ghz, in indoor environments of commercial buildings
Abstract: The practically unstoppable deployment of WLAN in the worldwide, both indoor and outdoor environments, requires the development of strategies, models, methods and techniques that increase accuracy in the planning and dimensioning process, in one of its main segments as radio propagation, thatit is closely related to the coverage prediction, in order to decrease the likelihood of oversized or undersized of such systems. Therefore, in this paper, it is developed a semi-empirical model for path loss prediction using the received power measurements in indoor environments performed on two commercial buildings of the Guayaquil city, Ecuador. The new model includes the signal attenuation when it to pass through floors and walls and a losses factor dependent of height transmitter as well considered a power loss exponent also related to that height. The developed model is compared with other existing models in the literature, in terms of the root mean square error (RMSE), showing a better performance of that model in all measurement scenarios considered.
Keywords: Wireless LAN, path loss propagation, indoor environments, semi-empirical model
Recibido (01/07/15), aceptado (16/11/15)
I. INTRODUCCIÓN
Desde su advenimiento en la década de los años 90 [1], las redes inalámbricas de área local (WLAN= Wireless Local Area Network), también conocidas como redes IEEE 802.11, se han convertido en una de las alternativas más atractivas para la transmisión de datos, especialmente para los usuarios, debido a las ventajas inherentes a toda comunicación inalámbrica y a los bajos costos para el acceso a dichas redes, esta última, producto principalmente de la operación de redes WLAN en las bandas de frecuencias llamadas libres o no licenciadas, tales como ISM (Industrial, Scientific and Medical) [1] y banda green-field [2].
Actualmente, las redes WLAN copan el escenario con estándares IEEE 802.11 de reconocida madurez tecnológica, tales como IEEE 802.11a [3], IEEE b/g [4] e IEEE 802.11n [5,6], así como algunos considerados como emergentes, tal es el caso de IEEE 802.11ad [7], IEEE 802.11ac [8,9], IEEE 802.11af [10], IEEE 802.11ah [11], entre otros.
Ahora bien, para garantizar el mejor desempeño posible de dichos estándares una vez puestos en operación, es necesariollevar a cabo previamente un adecuado proceso de planificación y dimensionamiento (PyD), entre cuyas principales aristas está el segmento de radiopropagación, enfocado especialmente a la estimación de la cobertura de los APs (Access Point) o enrutadores inalámbricos encargados de transmitir la señal RF (radiofrecuencia) hasta los usuarios. Para ello, se cuenta en la literatura con diversos modelos que permiten predecir las pérdidas de propagación de acuerdo a las características técnicas de los equipos, los requerimientos de desempeño y las características de radiopropagación de los entornos físicos. Sin embargo, para el caso específico de las redes WLAN operando en 2,4GHz y 5,8GHz (por ejemplo, IEEE 802.11n), ninguno de esos modelos ha sido desarrollado considerando las características típicas de propagación, por ejemplo, de ambientes interiores de edificios comerciales de la ciudad de Guayaquil, Ecuador, por lo que la aplicación de cualquiera de esos modelos en la planificación y dimensionamiento de redes WLAN en dichos entornos introducirá errores en la predicción de la cobertura de la red a ser implementada, que pudieran redundar en un sobredimensionamiento o sub-dimensionamiento de la misma.
En ese sentido, en este trabajo se desarrolla un modelo de propagación para las bandas de frecuencia de 2,4GHz y 5,8GHz, basado en mediciones realizadas en ambientes interiores de un par de edificios comerciales de la ciudad de Guayaquil, Ecuador; modelo que también podrá ser utilizado para la estimación de las pérdidas de propagación en ambientes interiores similares.
En este artículo, primero se lleva a cabo una revisión bibliográfica acerca de algunos de los modelos de propagación reportados en la literatura para ambientes interiores. Seguidamente, se describe el setup experimental (conjunto de equipos y herramientas auxiliares) utilizado para las mediciones, para posteriormente reseñar los ambientes y rutas o caminos seleccionados para la realización de dichas mediciones y luego presentar los principales resultados obtenidos. En seguida, se desarrolla el modelo como tal, y finalmente, se compara el desempeño del modelo desarrollado con el de algunos de los modelos de la literatura.
II. DESARROLLO
1. Modelos de Propagación en Ambientes Interiores para 2,4 GHz y 5,8 GHz
Para la predicción de las pérdidas de propagación en ambientes interiores en frecuencias de 2,4 GHz y 5,8 GHz existen diversos modelos reportados en la literatura, clasificados principalmente en determinísticos y semi-empíricos. Los primeros son basados en la técnica de trazado de rayos [12,13], método FDTD (Finite Difference Time Domain) [14,15], Teoría Uniforme de la Difracción (UTD = Uniform Theory of Diffraction) [16], Método de los Momentos (MoM = Method of Moments) [17], ecuaciones parabólicas [18], entre otros, que si bien resultan más precisos en la predicción de las pérdidas de propagación, por basarse en mayores detalles físicos del ambiente, prácticamente pueden ser aplicados sólo en entornos muy similares a los utilizados para su desarrollo. Por su parte, los modelos semi-empíricos, basados en la obtención de ecuaciones que se ajusten a mediciones de campo, a pesar de no ser tan precisos en su estimativa de las pérdidas, presentan la ventaja de ser menos complejos para su desarrollo, debido a que no son afectados de manera tan crítica por las singularidades del ambiente; además, son aplicables a una mayor diversidad de ambientes, sin que los mismos necesariamente tengan que presentar una alta similitud con los utilizados en el desarrollo del modelo. En esta sección se describen de manera sucinta algunos de los modelos de propagación semi-empíricos más utilizados en la literatura para ambientes interiores aplicables para las frecuencias de 2,4 GHz y 5,8 GHz.
A. Modelo Log-distance
Desarrollado para ambientes interiores y exteriores, es uno de los modelos más clásicos. Está basado en la ley de potencia con la distancia, según la cual las pérdidas de propagación aumentan con el logaritmo (de base 10) de la distancia, dependiendo del valor del exponente de pérdidas n. La atenuación es dadas por [19,20]:
![]()
Donde:
d = Distancia transmisor-receptor (km)
L(do) = Pérdidas de propagación (dB) a una distancia do
do = Distancia de referencia (km) (para ambientes interiores, generalmente es igual a 0,001km)
Xσ = Variable aleatoria (gaussiana o normal), en dB, con media igual a cero y desviación estándar igual a σ, también en dB. Esta variable describe el comportamiento estadístico de las pérdidas de propagación para distancias mayores a do
Las pérdidas L(do) se calculan utilizando el modelo de pérdidas en el espacio libre o a través de mediciones de campo realizadas a la distancia do. En todo caso, el modelo de propagación de espacio libre es representado por [21]:
Lel(dB) = 92,44 + 20 log f + 20 log d (2)
Donde f es la frecuencia de operación en GHz.
El exponente de pérdidas n y la desviación estándar σ, dependen de la frecuencia de operación e implícitamente de las características físicas (tipos de entornos interiores, disposición de los elementos físicos presentes en esos entornos, tipos de material de construcción, etc.) inherentes al camino o ruta de medición. En [19] se presentan valores n, los cuales varían desde 1,6 (para una frecuencia de 1,3 GHz y un ambiente industrial de metalurgia con línea de vista entre transmisor y receptor) hasta 3,3 (para la misma frecuencia y el mismo ambiente, pero con obstrucción total entre transmisor y receptor). Asimismo, de [19] se pueden obtener los valores de σ, los cuales varían desde 5,2 dB (para una frecuencia de 914 MHz y un ambiente correspondiente a una tienda expendedora de alimentos) hasta 14,1 dB (para un ambiente de oficinas con divisiones delgadas y una frecuencia de 1,9 GHz).
Unas de las variantes más usadas del modelo log-distance incorpora un factor de atenuación (FAF =Floor Attenuation Factor) debido a la presencia de pisos en el camino de la señal entre transmisor y receptor, así como un factor de pérdidas adicional, α, con la distancia. La variante en cuestión es conocida como modelo de Devasirvatham [22].
B. Modelo de ITU-R para ambientes interiores.
Válido para el rango de frecuencias comprendido entre 900 MHz y 100 GHz, es un modelo exclusivo para la estimación de las pérdidas de propagación en ambientes interiores. De manera implícita, el modelo considera las pérdidas a través del mobiliario, puertas y paredes, a través del exponente de pérdidas n que depende del tipo de edificios (residencial, comercial, de oficinas, etc.). Asimismo, toma en cuenta, de forma explícita, las pérdidas a través de pisos. En resumen, las pérdidas de propagación en el referido modelo se determinan a partir de [23]:
![]()
Donde:
N = 10n, obtenido de la Tabla 2 [23]
d = Distancia entre transmisor y receptor, en metros (d > 1 m).
do = Distancia de referencia (igual a 1 m)
L(do) = Pérdidas (dB) para una distancia de referencia do igual a 1 m. Asumiendo, propagación en espacio libre, entonces L(do) = 20 logf – 28 (con f en MHz)
Nf = Número de pisos atravesados por la trayectoria directa (para Nf = 0, resulta Lf = 0 dB)
Lf = Factor de pérdidas por penetración en pisos (dB), que además de depender de Nf, también depende de la frecuencia (se obtiene de la Tabla 3 de [23])
C. Modelo Keenan-Motley.
También aplica sólo para ambientes interiores y considera pérdidas en el espacio libre adicionadas a pérdidas producidas por la presencia de paredes y pisos en la trayectoria directa de la señal entre transmisor y receptor. Para el modelo en cuestión, la atenuación total de la señal es dada por [24]:
L(dB) = Lel+ Lc+ (ΣIi=1Nf,iLf,i + ΣJj=1Nw,jLw,j) (4)
Donde:
Lel = Pérdidas en el espacio libre (dB), calculadas a partir de la expresión (2)
Lc = Constante (empírica) (dB)
Lf,i = Pérdidas de propagación (dB) a través de los pisos
Nf,i = Número de pisos con las mismas características
Lw,j = Pérdidas de propagación (dB) a través de paredes
Nw,j = Número de paredes con las mismas características.
I = Número de tipos de pisos atravesados por la señal
J = Número de tipos de paredes atravesadas por la señal
El factor Lc es obtenido mediante regresión lineal aplicada a mediciones sobre pérdidas en paredes y pisos. Adicionalmente, también incluye otros efectos en la señal que se está propagando, como por ejemplo, el del mobiliario. En [24] se pueden conseguir algunos valores de Lc para diferentes tipos de paredes en cuanto al material de construcción y espesor, obtenidos a partir de mediciones realizadas en una frecuencia de 2,45 GHz.
Existe una versión simplificada del modelo Keenan- Motley para el caso de no contar con la suficiente información sobre los tipos de paredes y pisos. Esta versión, que considera un único tipo de piso y hasta dos (2) tipos de paredes, permite calcular las pérdidas de propagación mediante [25]:
L(dB)= 37 + 20 logd + NfLf+Σ2j=1Nw,jLw,j (5)
Donde:
Nf = Número de pisos atravesados
Lf = Pérdidas de propagación (dB), a través de los pisos
Lw,1= Pérdidas de propagación (dB), en paredes ligeras de madera, puertas, etc.
Lw,2 = Pérdidas de propagación (dB), en paredes gruesas, tabiques de ladrillo, cemento, etc.
Típicamente, Lf varía entre 13 dB y 27 dB, Lw,1 de 2 dB a 4 dB y Lw,2 entre 8 dB y 12 dB [25].
D. Modelo COST 231 Multi-Wall
Desarrollado sólo para entornos interiores, considera una componente de pérdidas que es proporcional al número de paredes atravesadas, pero asume una dependencia no lineal entre la atenuación total, causada por múltiples pisos y el número de pisos atravesados, que aumenta más lentamente, para pisos adicionales, después del primer piso atravesado. Las pérdidas de propagación se determinan de [26]:
![]()
Donde Nf es el número de pisos atravesados y los factores Lc y b dependen del ambiente interior considerado y son obtenidos por regresión lineal a partir de mediciones experimentales, siendo valores típicos Lc= 37 y b = 0,46 [27].
Por su parte, de modo general, para un ambiente de oficinas el exponente de pérdidas n es considerada igual a 4 y ambiente interior menos pesimista puede ser igual a 3 [27], mientras que un valor típico para Lf es 18,3 [27].
E. Modelo Venezuela
Basado en mediciones realizadas en ambientes interiores de la Universidad Experimental del Táchira (UNET), ubicada en la ciudad de San Cristóbal, Venezuela, en la frecuencia de 2,4 GHz, es un modelo de propagación que incluye la atenuación de la señal debida hasta seis paredes y un piso. Adicionalmente, incorpora un factor de incremento de las pérdidas que depende directamente de la altura del transmisor en la estimación de las pérdidas totales, las cuales son dadas por [28]:
L(dB) = -56,11 + 29,71h + (74,33 - 21,40h)log(d) + Lf1 + Lw (7)
Donde h se refiere a la altura del transmisor (en metros), Lf1 es igual 14,94 dB y Lw implícitamente depende del número de paredes atravesadas, variando desde 2,46 dB (cuando la señal atraviesa la primera pared) hasta 14,92 dB (cuando la señal atraviesa seis paredes) [28].
Además, se puede observar que en el modelo Venezuela, el exponente de pérdidas también depende de la altura del transmisor.
2. Equipo Utilizado para las Mediciones.
Como transmisores fueron utilizados dos (2) APS (Access Point). Para la banda de frecuencia de 2,4 GHz se empleó un AP con una potencia de transmisión de 20 dBm y una ganancia de la antena interna de 5 dBi, mientras que para las mediciones en la frecuencia de 5,8 GHz el AP utilizado tenía una potencia de transmisión de 30 dBm y una antena interna con ganancia también a 5 dBi. Para ambos transmisores las pérdidas de alimentación fueron consideradas iguales a 0 dB.
Fungiendo como receptor fue utilizado un computador portátil con tarjeta de red inalámbrica incorporada. Para la captura del nivel de señal recibido (potencia recibida) se recurrió a la herramienta computacional InSSIDer [29].
Es importante resaltar que, las mediciones fueron realizadas a partir de una distancia, en este caso un (1) metro, que garantizase que los puntos de medición estuviesen siempre en la región de campo lejano de la antena, es decir, aquella en la cual la onda electromagnética es plana, no es afectada por su fuente de radiación (antena) y tiene sus campos eléctrico y magnético fuertemente acoplados entre sí. Por tanto, en dicha región, para obtener mediciones fiables de la potencia recibida es suficiente con considerar sólo el campo eléctrico, al que está asociada directamente la potencia recibida [30, 31].
3. Ambientes y Rutas Seleccionadas para las Mediciones.
Las mediciones fueron implementadas en dos entornos interiores, que aquí serán denominados Ambiente 1 y Ambiente 2, localizados en la ciudad de Guayaquil, Ecuador. El Ambiente 1 correspondió a uno los estacionamientos del sótano de un centro comercial, en un área contigua a locales comerciales. El Ambiente 2 consistió en dos pisos consecutivos de un área de oficinas situados en un edificio comercial.
Ambiente 1
En este Ambiente 1 fueron realizadas las siguientes mediciones:
Medición 1: Nivel de potencia recibida versus distancia, línea de vista, frecuencia igual a 2,4 GHz, altura del AP igual 2,5 m.
Medición 2: Nivel de potencia recibida versus distancia, presencia de paredes en la ruta de medición, frecuencia igual a 2,4 GHz, altura del AP igual a 2,5 m (ruta paralela a la de la Medición 1).
Medición 3: Nivel de potencia recibida versus distancia, línea de vista, frecuencia de 2,4 GHz, alturas variables del AP (es el mismo camino de la Medición 1, pero variando la altura del AP entre 2,2 m y 2,5 m).
Medición 4: Similar al caso de la Medición 3, pero para una frecuencia de 5,8 GHz.
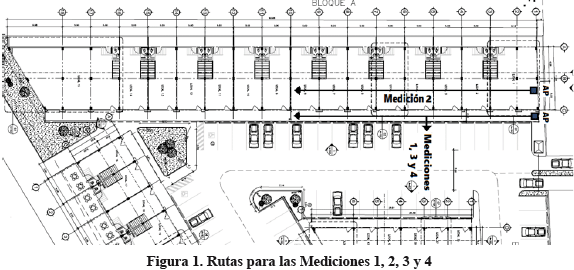
En la Figura 1, se muestra el plano del Ambiente 1, así como las rutas correspondientes a cada una de las cuatro mediciones realizadas en el mencionado ambiente.
Ambiente 2
Las mediciones realizadas en este Ambiente 2 fueron:
Medición 5: Nivel de potencia recibida versus distancia, presencia de paredes en la ruta de medición, frecuencia iguala 2,4 GHz, altura del AP igual a 2,5 m, piso 2.
Medición 6: Nivel de potencia recibida versus distancia, presencia de paredes y un piso en la ruta de medición, frecuencia igual a 2,4 GHz, altura del AP igual a 2,5 m, piso 3.
Medición 7: similar al camino de Medición 5, pero con frecuencia igual a 5,8 GHz.
Medición 8: similar al camino de Medición 6, pero con frecuencia igual a 5,8 GHz.
En las Figuras 2a y 2b, se puede observar el plano correspondiente al Ambiente 2 junto con las cuatro rutas de mediciones llevadas a cabo dicho ambiente.
4. Resultados de las Mediciones.
A. Pérdidas de propagación en función de la distancia y la frecuencia.
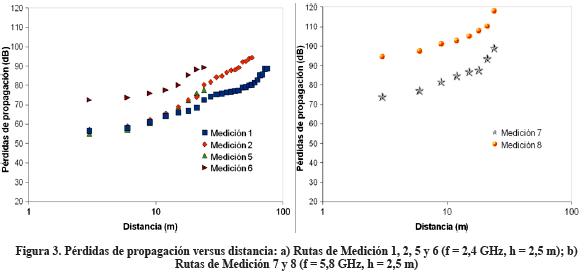
En la Figura 3a se muestran los gráficos de dispersión de las pérdidas de propagación, en función de la distancia, para las rutas de Medición 1 y 2 (Ambiente 1), con frecuencia de operación de 2,4 GHz y altura h del AP de 2,5 m. Asimismo, en la Figura 3a también se pueden observar los gráficos de dispersión para los caminos de Medición 5 y 6 (Ambiente 2), con igual frecuencia de operación y misma altura del AP.
Por su parte, en la Figura 3b, aparecen los gráficos de dispersión de las pérdidas de propagación en función de la distancia, para las rutas de Medición 7 y 8 medidas en el Ambiente 2, con una frecuencia de operación de 5,8 GHz y altura del AP de 2,5 m.
En las Figuras 3a y 3b, se observa que, como era de esperarse, las pérdidas de propagación aumentan a medida que la distancia entre el transmisor y el receptor también incrementa. Además, se percibe que el camino de Medición 1 es el que presenta menos pérdidas, lo cual se debe a que es un camino con línea de vista y además corresponde a la frecuencia de operación más baja de las dos consideradas (2,4 GHz), contrariamente a lo observado en la ruta de Medición 8, en la cual se obtuvieron las mayores pérdidas, debido a que, además de tratarse de una trayectoria de la señal obstruida por algunas paredes y un piso, la medición fue realizada a la frecuencia superior, es decir, 5,8 GHz. Asimismo, se puede notar que las líneas de tendencia de cada curva pueden ser aproximadas a una recta.
Es importante destacar que, las pérdidas de propagación de la Figura 4 fueron estimadas a partir del nivel de señal recibido en cada punto de medición, a partir de [32]:
L(dB) = PT + GT + GR + LT + LR + PR (8)
Donde:
PT = Potencia transmitida (dBm)
GT,R = Ganancias de la antenas del transmisor y receptor, respectivamente (dBi)
LT,R = Pérdidas en las líneas de transmisión del transmisor y del receptor, respectivamente (dB)
PR = Nivel de señal recibido
B. Pérdidas de propagación en función de la altura del transmisor.
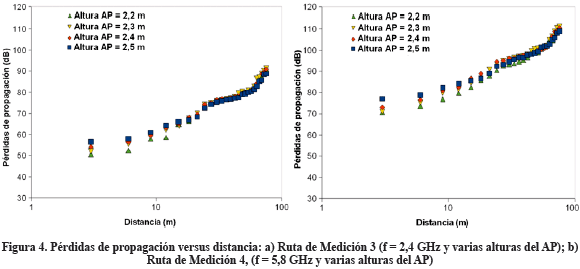
Los resultados obtenidos para la variación de las pérdidas de propagación en función de la altura del AP, son mostrados en las Figuras 4a y 4b. Para ello, se consideraron lasrutas de Medición 3 y 4 (Ambiente 1), con frecuencia de operaciones iguales a 2,4 GHz y 5,8 GHz, respectivamente. Las alturas consideradas para del AP fueron 2,2 m, 2,3 m, 2,4 m y 2,5 m.
En las Figuras 4a y 4b se puede apreciar nuevamente el aumento de las pérdidas de propagación con la distancia, así como la tendencia de línea recta de todas las curvas. Asimismo, una vez más se aprecia el aumento de las pérdidas con la frecuencia. Adicionalmente, se nota que, en general, el comportamiento de dicha pérdida con la altura es similar para los cuatro (4) valores de h considerados para la medición, para una misma frecuencia. Empero, se puede verificar que la tendencia lineal correspondiente a cada h tiene una pendiente que disminuye con el que aumento de dicho parámetro, es decir, se verifica que las pérdidas de propagación también varían con la altura del transmisor.
C. Variación de las pérdidas de propagación con la presencia de paredes y pisos.
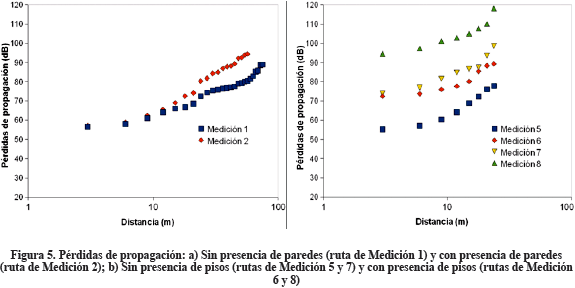
La comparación más clara que permite observar el comportamiento de las pérdidas de propagación con las paredes es la referida a las rutas de Medición 1 y 2, los cuales son aproximadamente las mismas rutas físicas, con la misma frecuencia de operación (2,4 GHz) y misma altura h (2,5 m), pero con la diferencia que la ruta de Medición 1 corresponde al caso de línea de vista, mientras que en la otra ruta la trayectoria directa de la señal atraviesa paredes. La Figura 5a ilustra la referida comparación, en la que se puede percibir que las pérdidas en la ruta de de Medición 2 son mayores que en el camino de Medición 1, a partir de la presencia de la primera pared, es decir, después de una distancia de aproximadamente 9 m del transmisor.
Por su parte, las pérdidas en pisos, que en estas mediciones fue uno (1), se pueden observar en la Figura 5b, en la que se compara el comportamiento de dichas pérdidas en las rutas de Medición 5 y 6, así como las rutas de Medición 7 y 8, que corresponden a mediciones en pisos paralelos, uno arriba del otro, para las frecuencias de operación de 2,4 GHz y 5,8 GHz, respectivamente. Se experimentan mayores pérdidas de propagación para las rutas de Medición 6 y 8, respecto a las rutas de Medición 5 y 7, respectivamente. En la Figura 5b también se verifica el incremento de las pérdidas de propagación a medida que aumenta la frecuencia.
5. Desarrollo del Modelo de Propagación para Ambientes Interiores.
En principio, se sigue un procedimiento similar al utilizado en [28], recurriendo a las rutas de Medición 3 y 4, en las cuales se midieron las pérdidas de propagación, para cada punto, con cuatro (4) alturas diferentes del AP, sin existencia de paredes y pisos en la trayectoria directa de la señal. Sin embargo, a diferencia de [28], dado que a las pérdidas de propagación se adiciona un factor dependiente de la frecuencia, para el ajuste de la ecuación correspondiente a una primera aproximación del nuevo modelo se emplean técnicas de regresión no lineal, tales como Quasi-Newton, Simplex, Hooke- Jeeves PatternMoves, RosenbrockPatternSearch, entre otras [33], las cuales fueron implementadas con el auxilio de la herramienta computacional STATISTICA [33].
Seguidamente, para incorporar las pérdidas por pisos, que en las mediciones objeto de este artículo sólo se pudo evaluar el efecto de un piso, se utilizan los resultados mostrados en la Figura 5b. De manera similar a [28], para cada punto de medición, se restan las pérdidas de propagación de la ruta de Medición 6 menos las de la ruta de Medición 5 (para la frecuencia de 2,4 GHz) y de forma similar se procede para los caminos de Medición 7 y 8.
Ahora bien, para tomar en cuenta las pérdidas por la presencia de las paredes, se recurre a los resultados mostrados en la Figura 5a y se aplica el mismo procedimiento seguido para el caso de presencia de un piso. Los incrementos de las pérdidas de propagación, Lw, debido a la presencia de Nw paredes en la trayectoria directa de la señal son mostrados en la Tabla I.
En la Tabla I, cada valor de LW corresponde a la pérdida acumulada que se debe adicionar a las pérdidas totales, dependiendo del número de paredes atravesadas por la señal RF en su recorrido directo entre transmisor y receptor. Sin embargo, a rigor, los factores LW que aparecen en la Tabla I son válidos para el ambiente correspondiente a la ruta de Medición 2, o similares, implementada en las mediciones realizadas en este trabajo. Por tanto, dado que en la práctica rara vez se tiene la posibilidad de contar con los factores de pérdidas de propagación por pisos y paredes, se procede a expresar el factor Lw como función solamente del número de paredes NW, resultando la ecuación final del nuevo modelo de propagación, dada por:
L(dB) = (-56,75 + 30,66h) + (72,15 - 19,15h)logd + 51,78logf + Lf1 + 1,37NW0,18 (9)
donde h y d están dadas en metros, f en GHz y el factor de pérdida, Lf1, por la presencia de un piso, para cada frecuencia, resultó ser 13,90 dB para la frecuencia de 2,4 GHz y 19,20 dB para la frecuencia de 5,8 GHz (se observa que la frecuencia de operación también afecta el valor del factor de incremento de las pérdidas de propagación debido a la presencia de pisos en la trayectoria directa de la señal).
6. Comparación de los Resultados.
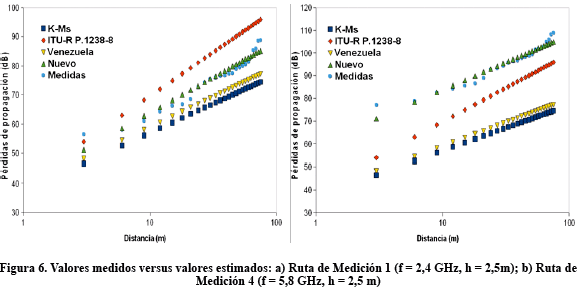
A fin de evaluar el desempeño del modelo aquí desarrollado, se procede a comparar los valores medidos de la pérdida de propagación, L, con los valores estimados por el modelo desarrollado y algunos de los modelos de propagación para ambientes interiores revisados en este artículo. En ese sentido, a modo de ejemplo, en las Figuras 6a y 6b se ilustra esa comparación para las rutas de Medición 1 (f = 2,4 GHz; h = 2,5 m) y Medición 4 (f =5,8 GHz; h = 2,5 m). En ese caso, en la expresión (9) Lf1 y NW son iguales a cero pues no existen ni pisos ni paredes.
En las Figura 6a y 6b, se observa que el nuevo modelo es el que mejor se ajusta a los valores medidos, mientras que para el caso de f igual a 2,4 GHz el modelo de ITU-R es el que aparentemente más se aleja (sobrestimando las pérdidas de propagación), a la vez que los modelos Keenan y Motley simplificado (que en la Figura 6a aparece como K-Ms) y Venezuela, subestiman dichas pérdidas. Para f igual a 5,8 GHz, se puede apreciar que los modelos Venezuela, Recomendación ITU-R P.1238- 8 y Keenan y Motley simplificado, subestiman las pérdidas de propagación, con el más bajo desempeño en sus estimaciones para los modelos Venezuela y Keenan y Motley simplificado.
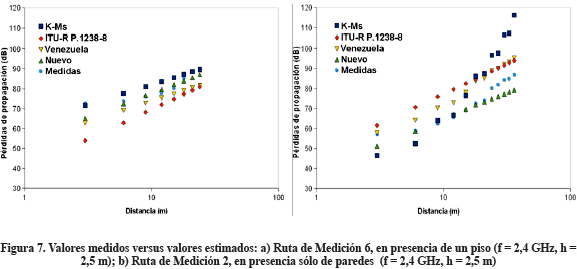
Para mostrar el desempeño del modelo ante la presencia de pisos en la trayectoria directa de la señal, en la Figura 7a aparecen los valores medidos y estimados para la ruta de Medición 6, que corresponden a la presencia de un piso. En este caso, Nw en la expresión (9) es igual a cero, debido a que el transmisor, que se colocó en el piso de abajo, se encontraba muy próximo al techo de dicho piso.
Por su parte, la Figura 7b permite percibir el desempeño de los modelos cuando existen paredes en la trayectoria directa de la señal RF, en cuyo caso se seleccionó la ruta de Medición 2 y se utilizó la expresión (9) con Lf1 igual a cero, al tratarse de un camino en un mismo piso.
En las Figuras 7a y 7b, se puede apreciar nuevamente el mejor desempeño del nuevo modelo en comparación con el arrojado por los restantes modelos incluidos en la comparación. No obstante, de acuerdo a la Figura 7a, correspondiente a la ruta de Medición 6, se puede observar que el desempeño del modelo Keenan y Motley simplificado también puede ser considerado como bastante aceptable. Por parte, en la Figura 7b, que se refiere a la ruta de Medición 2, se muestra que en el caso de presencia de paredes en el camino directo de la señal, el desempeño del nuevo modelo tiende a deteriorarse con el aumento de la distancia, pero a pesar de ello sigue siendo aparentemente mejor que el mostrado por los restantes modelos.
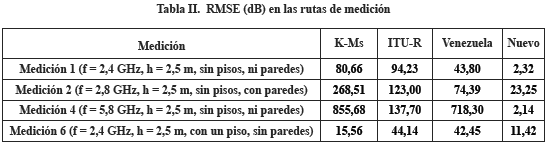
En todo caso, para cuantificar el desempeño de los modelos considerados en las comparaciones mostradas en las Figuras 6a, 6b, 7a y 7b, se determina la raíz cuadrada del error medio cuadrático (RMSE = Root Mean Square Error), los cuales se resumen en la Tabla II y permiten comprobar el mejor desempeño del nuevo modelo en todos los casos considerados. Nótese el desempeño también aceptable del modelo Keenan y Motley simplificado para la ruta de Medición 6, con un RMSE de 15,56 dB. Asimismo, obsérvese el RMSE más alto del nuevo modelo fue para la ruta de Medición 2.
Un resultado también interesante fue el obtenido en la ruta de Medición 8 (f = 5,8 GHz; h = 2,5 m), el cual arrojó valores de RMSE considerablemente mayores para los modelos Venezuela y Keenan y Motley simplificado (1022,45 dB y 383,13 dB, respectivamente), en comparación con los RMSE de dichos modelos en la ruta de Medición 6. Ello se debe a que el modelo Venezuela fue desarrollado sólo para la frecuencia de 2,4 GHz y el modelo Keenan y Motley simplificado fue obtenido para una frecuencia de 2,45 GHz.
III. CONCLUSIONES
En este artículo ha sido propuesto un nuevo modelo semi-empírico para estimar las pérdidas de propagación en redes WLAN operando en las frecuencias de 2,4 GHz y 5,8 GHz, en ambientes interiores de edificios comerciales de la ciudad de Guayaquil, Ecuador. Se consideró como variable dependiente la potencia recibida y como variables independientes la distancia transmisor-receptor, frecuencia de operación y altura del transmisor. El modelo también incluye factores de atenuación de la señal debido a la presencia de pisos y paredes en la trayectoria directa de la señal. Para el ajuste de ecuación del mencionado modelo se recurrió a técnicas de regresión no lineales.
El desempeño del nuevo modelo en la predicción de las pérdidas, comparado en términos del RMSE, con los modelos de modelos de propagación Venezuela, Keenan y Motley simplificado y Recomendación ITU-R P.1238-8, resultó siempre mejor en todos los casos de estudio considerados.
REFERENCIAS BIBLIOGRÁFICAS
1. Berg J. The IEEE 802.11 Standardization. Its History, Specifications, Implementations, and Future. Technical Report GMU-TCOM-TR-8, George Mason University, Fairfax, VA, USA, 2011. [ Links ]
2. Grieve D. (2012). IEEE 802.11ad PHY Layer Testing. Agilent Technologies. Documento en línea, disponible en http://www.keysight.com/upload/cmc_upload/All/WirelessSymp802_11adPHY.pdf? & cc=VE & lc=eng (consultado en enero 2016). [ Links ]
3. Tektronix (2013). Wi-Fi: Overview of the 802.11 Physical Layer and Transmitter Measurements. Documento en línea, disponible en http://www.cnrood.com/public/docs/WiFi_Physical_Layer_and_Transm_Meas.pdf (consultado en enero 2016). [ Links ]
4. Bastidas E, Ordoñez L. Propuesta de Diseño de una Red Inalámbrica 802.11b/g en la Universidad de Pinar del Río con Análisis de Cobertura y de Seguridad. Tesis, Ingeniero en Teleinformática, Universidad Técnica de Cotopaxi, Latacunga, Ecuador, 2010. [ Links ]
5. Leandro W.A. Comparativo entre IEEE 802.11g e 802.11n. 2012. Monografia, Especialização em Configuração e Gerenciamento de Servidores e Equipamentos de Rede, Universidade Tecnológica Federal do Paraná, Curitiba, Brasil, 2012. [ Links ]
6. Cuesta V., Romero C. Evaluación de Tecnología IEEE 802.11n en Redes de Larga Distancia. Trabajo de Fin de Titulación, Ingeniero en Electrónica y Telecomunicaciones, Universidad Técnica Particular de Loja, Ecuador, 2013. [ Links ]
7. Perahia E., Gong M. Gigabit Wireless LANs: An Overview of IEEE 802.11ac and 802.11ad. ACM SIGMOBILE Mobile Computing and Communications, Vol. 15, pp. 23-33, July 2011. [ Links ]
8. Siddiqui F., Zeadally S., Salah K. Gigabit Wireless Networking with IEEE 802.11ac: Technical Overview and Challenges. Journal of Networks, Vol. 10, No. 3, pp. 164-171, April 2015. [ Links ]
9. Shah Z., Rau S., Baig A. Throughput Comparison of IEEE 802.11ac and IEEE 802.11n in an Indoor Environment with Interference. 2015 International Telecommunication Networks and Applications Conference (ITNAC), Sydney, Australia, pp. 196-201, November 2015. [ Links ]
10. Hu H., Kaleshi D., Doufexi A., Li L.Performance Analysis of IEEE 802.11af Standard based Neighbourhood Area Network for Smart Grid Applications. IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, Scotland, UK, pp. 1-5, May 2015. [ Links ]
11. Sthapit P., Subedi S., Kwon G.R., Pyun J.Y. Performance Analysis of Association Procedure in IEEE 802.11ah. 10th International Conference on Systems and Networks Communications (ICSNC 2015), Barcelona, Spain, pp. 70-73, November 2015. [ Links ]
12. Dama Y., et al. MIMO Indoor Propagation Prediction using 3D Shoot-and-Bounce Ray (SBR) Tracing Technique for 2.4 GHz and 5 GHz. 5th European Conference on Antennas and Propagation (EUCAP), Rome, Italy, pp. 1655.1658, April 2011. [ Links ]
13. Soe T.W., Aye A.M. Indoor Radio Wave Propagation with Ray Tracing Technique. International Journal of Advances in Electronics and Computer Science, Vol. 2, No. 6, pp. 7-11, June 2015. [ Links ]
14. Sosa J., et al. Indoor 2.4 GHz Microwave Propagation Study using 3D FDTD Approach. Electronics Letters, Vol. 47, No. 24, pp. 1308-1309, November 2011. [ Links ]
15. Yamaguti S. ,Yonezawa S., Omiya M. Estimations of Indoor Propagation Characteristic at 5 GHz Band for IEEE802.11n Wireless LAN. International Symposium on Antennas & Propagation (ISAP 2014), Kaohsiung, Taiwan, pp. 577-578, December 2014. [ Links ]
16. Bernardi P., Cicchetti R., Testa O. An Accurate UTD Model for the Analysis of Complex Indoor Radio Environments in Microwave WLAN Systems. IEEE Transactions on Antennas and Propagation, Vol. 52, No. 6, pp. 1509-1520, June 2004. [ Links ]
17. Mitilineos S.A., Pnagiotou S.C., Varlamos P.K., Capsalis C.N. Indoor Environments Propagation Simulation using a Hybrid MoM and UTD Electromagnetic Method. Annales Des Télécommunications, Vol. 60, No. 9-10, pp. 1231-1243, October, 2005. [ Links ]
18. Barauna F.N., Souza J.F. Cozzolino K., Costa J.C., Santos G.P. A Model for Radio Propagation Loss Prediction in Buildings using Wide-angle Parabolic Equations. SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC 2009), Belem, Brasil, pp. 491- 495, November 2009. [ Links ]
19. Andersen J.B., Rappaport T.S., Yoshida S. Propagation Measurements and Models for Wireless Communications Channels. IEEE Communications Magazine, Vol. 33, No. 1, pp. 42-49, January 1995. [ Links ]
20. Rappaport T.S. Wireless Communications: Principles and Practice. 2nd Edition, Prentice Hall, 2002. [ Links ]
21. Parsons J.D. The Mobile Radio Propagation Channel. 2nd Edition, John Wiley & Sons, 2000. [ Links ]
22. Devasirvatham D.M.J., Banerlee C., Krain M.J., Rappaport D.A. Multi-frequency Radiowave Propagation Measurements in the Portable Radio Environment. IEEE International Conference on Communications (ICC '90), Atlanta, GA, USA, pp. 1334-1340, April 1990. [ Links ]
23. International Union Telecommunications. ITU-R P.1238-8 Recommendation: Propagation Data and Prediction Methods for the Planning of Indoor Radiocommunication Systems and Radio Local Area Networks in the Frequency Range 900 MHz to 100 GHz. Geneva, Switzerland, 2015. [ Links ]
24. Nagy L. Indoor Radio Network Optimization, in Communications and Networking, Peng J. Rijeka, Croatia: Sciyo Publisher, 2010, pp. 237-262. [ Links ]
25. Hernando J.M. Comunicaciones Móviles. 2ª Edición, Editorial Universitaria Ramón Areces, 2004. [ Links ]
26. Alhamoud A., et al. Empirical Investigation of the Effect of the Doors State on Received Signal Strength in Indoor Environments at 2.4 GHz. IEEE 39th Conference on Local Computer Networks Workshops (LCN Workshops), Edmonton, Canada, pp. 652-657, September 2014. [ Links ]
27. Cranley N. Model for Wireless LAN Transmitter Location for Optimal Performance. Dissertation of Master of Science, Computing for Commerce and Industry, The Open University, England, UK, 2004. [ Links ]
28. Pérez-Garcia N., Pabón C., Uzcátegui J.R., Malaver E. Nuevo Modelo de Propagación para Redes WLAN operando en 2.4 GHz, en Ambientes Interiores. Telematique, Vol. 9, No. 3, pp. 1-22, Septiembre- Diciembre 2010. [ Links ]
29. InSSIDer. Tiene bastante Preocupaciones, y Ahora el Wi‑Fi no Funciona. Documento en línea, disponible en http://www.inssider.com/es/inssider/ (consultado en junio 2015). [ Links ]
30. Duguay D. Guidelines for the Measurement of Radio Frequency Fields at Frequencies from 3 kHz to 300 GHz. Industry Canada, Ottawa, Canada, 2015. [ Links ]
31. Dlugosz T., Trzaska H. How to Measure in the Near Field and in the Far Field. Communication and Network, Vol. 2, No. 1, pp. 65-68, February 2010. [ Links ]
32. Pérez-García N. Cálculo de Cobertura de Sistemas WLL e LMDS. Dissertação de Mestrado em Engenharia Elétrica, Pontifícia Universidade Católica do Rio de Janeiro (PUC/Rio), Brasil, Abril 2000. [ Links ]
33. Dell Software. Statistica - Download Software. Documento en línea, disponible en https://support.software.dell.com/statistica/download-new-releases (consultado en noviembre 2015). [ Links ]












 uBio
uBio