Barrido de un mecanismo de rastrillo clasificador en función del ajuste individual de sus cinco paramétros geométricos calibrables

Jesús Alberto Mendoza Quiñonez¹, Lácides Rafael Pinto², Olenka Gómez Julio³

¹Universidad Nacional Experimental Politécnica "Antonio José de Sucre", Vicerrectorado Puerto Ordaz jmendoza@unexpo.edu.ve ;

^2,3Universidad de La Guajira. Riohacha. Colombia. Ciudadela Universitaria. lpintom@uniguajira.edu.co; ogomezjulio@uniguajira.edu.co

Resumen:

El presente trabajo muestra la trayectoria que describe el extremo del diente final de barrido en la zona de descarga de un mecanismo de rastrillo clasificador fabricado por Dorr-Oliver. Se lleva a cabo porque es necesario conocer cómo el ajuste individual de los cinco parámetros geométricos de calibración del mecanismo, modifica tanto la carrera de avance y retroceso del rastrillo como la altura a la que el rastrillo pasa respecto al fondo de la cuba de este dispositivo. Para graficar estas trayectorias se relacionan las seis coordenadas generalizadas de salida de los eslabones del mecanismo con la coordenada generalizada de entrada y con la magnitud de los veintisiete parámetros geométricos funcionales del mecanismo, dentro de los cuales se encuentran los cinco parámetros geométricos ajustables. Luego, se determina en el campo de las posiciones, la ecuación cinemática vectorial que permite ubicar el extremo de descarga del rastrillo a medida que la coordenada generalizada de entrada varía entre 0° y 360°. Se puede comprobar que el extremo del rastrillo describe una familia de trayectorias ligeramente diferentes de acuerdo con el valor de cada ajuste individual de los parámetros geométricos calibrables. El trabajo permite reconocer cuáles parámetros geométricos ajustables son más significativos o no para la calibración y sirve como una carta gráfica práctica de rápida consulta para las labores de operación y mantenimiento.

Palabras Clave: Trayectorias de puntos, Rastrillo clasificador de Dorr-Oliver, Calibración de mecanismos, Eslabones ajustables.

Rake classifier path as a function of the individual adjustment of its five calibration parameters

Abstract:

This paper shows a detailed calculation of the path of the rake on the sediment discharge end of a Dorr-Oliver rake classifier. This work is carried out in order to find the way in which the individual adjustment of the five calibration parameters of the mechanism modifies both the forward/backward stroke length and the distance from the rakes to the bottom of the slurry pool. To graph these paths, the six generalized output coordinates of the mechanism’s links are expressed as a function of the generalized input coordinate and the magnitude of the twenty-seven functional geometric parameters, which include the five calibration parameters. Subsequently, the kinematic vectorial equation is determined within the position field. This equation allows to locate the rake’s discharge end as the generalized input coordinate varies between 0º and 360º. Since the rake describes a set of slightly different paths depending on the individual adjustment of each calibration parameter, it is then possible to know which adjustable geometric parameter is more significant towards the calibration of the machine, which also serves as a fast graphical reference in case it is necessary to adjust the mechanism after maintenance.

Keywords: Point path, Rake Classifier, Mechanism calibration, Adjustable links.

Recibido (06/10/16), aceptado (12/12/16)

I. INTRODUCCIÓN

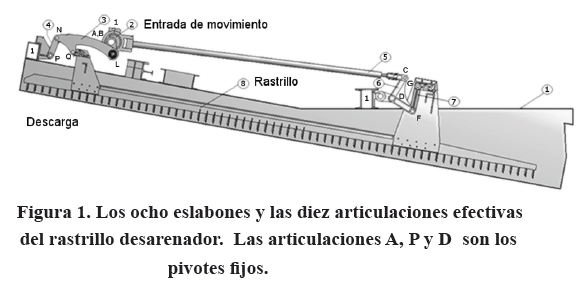
El rastrillo clasificador estudiado en este trabajo, también conocido como rastrillo desarenador, consiste de siete eslabones móviles más un bastidor. Un esquema a escala del eslabonamiento y de la cuba fija visto desde el lado motor, se muestra en la Figura 1. El elemento de salida del mecanismo es propiamente el rastrillo desarenador, numerado como 8. El rastrillo, de 7 m de largo, dispone de sesenta y nueve (69) dientes de barrido a lo largo de toda su longitud. Todas las articulaciones A, B, C, D, G, F, L, N, P y Q son rotatorias. En particular, las tres articulaciones A, P y D son los pivotes fijos del mecanismo durante el funcionamiento.

El rastrillo 8 se mueve con velocidad angular prácticamente nula y todos sus puntos describen una traslación curvilínea compleja. La inclinación del rastrillo durante el funcionamiento, es ligeramente menor que la inclinación de 10° de la cuba, como se observa en la figura 1 en la que los dientes lucen ligeramente más distantes del fondo de la cuba en su extremo derecho que en su extremo izquierdo. Este mecanismo es usado para recuperar sedimentos reusables en el proceso Bayer de Bauxilum. En la carrera de avance, los dientes del rastrillo se sumergen en el líquido lleno de barro que corre hacia abajo por el plano inclinado de la cuba, mientras que el rastrillo represa y arrastra hacia arriba en dirección de la boca de descarga, el barro que desciende. Una vez barrido el barro, el rastrillo retrocede sin trabajar para volver a posicionarse al inicio de la carrera de avance y volver a repetirse el proceso con una frecuencia de 15 ciclos por minuto.

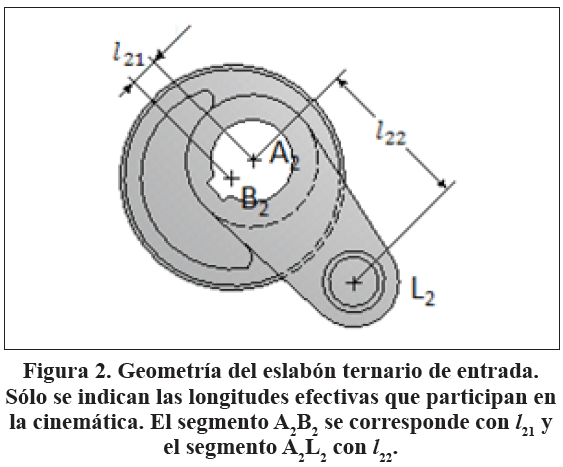
En este mecanismo, el eslabón de entrada 2, representado en la Figura 2, es una manivela doble que gira en sentido horario, constituida por una excéntrica y una palanca. Esta manivela tiene tres nodos cinemáticos A₂, B₂ y L₂ y en ella, los segmentos A₂B₂ y B₂L₂ son perpendiculares entre sí.

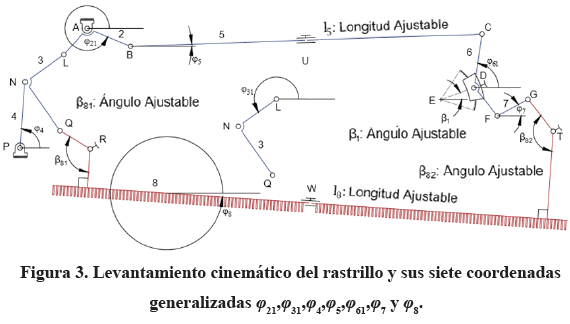
La Figura 3 es el esquema del levantamiento cinemático del mecanismo desde el lado motor. En esta representación se sigue las reglas de la IFToMM para la designación de las coordenadas generalizadas y los parámetros geométricos del mecanismo [1]. Se han enumerado con números los ocho elementos constituyentes del eslabonamiento y con letras mayúsculas los pares cinemáticos. La numeración empieza por el eslabón bastidor, numerado como 1 y sigue con el eslabón ternario de entrada, numerado como 2. El eslabón 3 es una biela ternaria, el 4 es un eslabón binario pivotado al bastidor en P. El 5 es un largo eslabón binario acoplador. El eslabón 6 es un eslabón ternario pivotado fijo al bastidor mediante un par especial rotatorio D que puede reposicionarse si se desea a una nueva posición fija a lo largo de un camino semicircular con centro en E y el eslabón 7 es una biela corta. El último eslabón es el rastrillo 8 que avanza y retrocede prácticamente en traslación curvilínea pura reciprocante para ejecutar el trabajo de barrido de sedimentos.

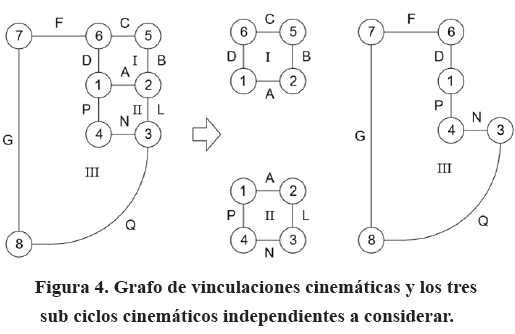
La Figura 4 es el grafo [2] de la cadena cinemática del mecanismo en el que cada eslabón se representa por un vértice y cada articulación cinemática por una arista que conecta los vértices correspondientes. Sirve para indicar cuáles eslabones se conectan con cuáles otros y a través de qué pares cinemáticos y para determinar el número de ciclos cinemáticos que se pueden trabajar de manera independiente para constituir posteriormente el conjunto de ecuaciones que rigen la cinemática.

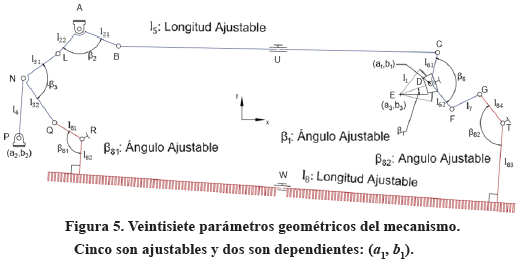
De acuerdo con el grafo, el eslabón 2 se conecta al bastidor mediante el par A, a 3 mediante el par L y a 5 mediante B. El eslabón 3, además de estar vinculado a 2 por el par rotatorio A, se vincula a 4 por medio del par rotatorio P y al rastrillo 8 por el par rotatorio Q. El eslabón 5, además de estar conectado con 2 por B, se conecta a 6 por el par rotatorio C. Por otra parte, además de estar conectado a 5 por C, el eslabón 6 está pivotado al bastidor mediante la articulación reposicionable D y al eslabón 7 mediante el par F. Finalmente, el rastrillo desarenador 8, está vinculado al eslabón 3 por Q y al eslabón 7 por G. En este esquema, E, R, T, U y W no son articulaciones durante el funcionamiento. E sirve para ajustar el ángulo β₁ en el bastidor. R y T sirven para ajustar los ángulos β₈₁y β₈₂ en el eslabón 8 y U y W para ajustar las longitudes de los eslabones 5 y 8. Una vez que se ajustan, los ángulos β₁,β₈₁ y β₈₂ y las longitudes l₅ y l₈ permanecen constantes durante la operación.

II. DESARROLLO

2.1 ANÁLISIS CINEMÁTICO

De acuerdo con la figura 3, el conjunto cuyos elementos son las siete coordenadas generalizadas que definen la posición angular q_i de todos los eslabones móviles de este mecanismo de palancas, está dado por (1).

{q_i} = {j₂₁, j₃₁, j₄, j₅, j₆₁, j₇, j₈}   (1)

Por otra parte, el conjunto {p_j} de veintisiete parámetros geométricos que definen la geometría funcional del mecanismo se representa en la Figura 4 y está dado en (2). Es de hacer notar que aunque el conjunto (2) tiene 27 parámetros geométricos, sólo 25 son independientes puesto que las coordenadas ajustables (a₁, b₁) del pivote D respecto al sistema de referencia ubicado en Axy, se obtienen a partir de las coordenadas (a₃, b₃) y de l₁, β₁ como se hará saber en las ecuaciones (7) y (8) que se muestran más adelante.

{p_j} = { l₂₁, l₂₂, β₂, l₃₁, l₃₂, β₃, l₄, a₂, b₂, l₅, l₆₁, l₆₂, β₆, l₇, a₃, b₃ , l₁, β₁, a₁ , b₁, l₈₁, l₈₂, β₈₁, l₈, l₈₃, l₈₄, β₈₂,} (2)

Cada uno de estos 27 parámetros geométricos del conjunto {pj} dado en (2) tiene asociado en la práctica una variación dimensional δp_j debido a múltiples factores [3], dentro de los cuales los más importantes son los errores de fabricación y montaje, las deformaciones debidas a la carga y las dilataciones térmicas [4]. Estas variaciones modifican la precisión deseada de funcionamiento [5], [6]. Por esta razón, el mecanismo se diseña para que los ajustes controlados longitudinales o angulares, según sea el caso, de los cinco parámetros geométricos de calibración del rastrillo, contrarresten estos inevitables errores.

Para poder graficar las trayectorias buscadas en función del ajuste de los cinco parámetros geométricos de calibración del mecanismo es necesario encontrar primero las ecuaciones cinemáticas vectoriales de restricción del movimiento en el campo de las posiciones {7] para cada uno de los tres sub circuitos cinemáticos que conforman el mecanismo. La solución de estas ecuaciones permitirá conocer la relación entre las coordenadas generalizadas dependientes de salida {φ₂₁,φ₃₁,φ₄,φ₅,φ₆₁,φ₇,φ₈} y la coordenada generalizada de entrada φ₂. Los ángulos relacionados con todas las coordenadas generalizadas, se medirán en sentido antihorario y respecto a la horizontal positiva, trazadas éstas en el origen de cada vector posición que sea necesario definir en cada lazo vectorial, según se indica en las Figuras 6, 7 y 8.

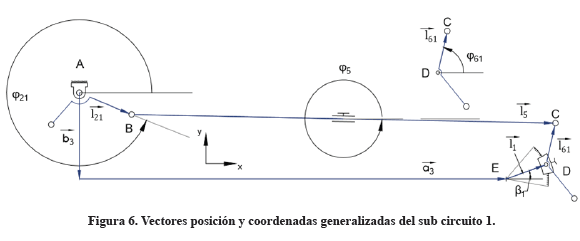
2.1.1 Sub circuito cinemático 1

El sub circuito cinemático arbitrariamente definido como sub circuito 1, mostrado en la Figura 5, está conformado por los eslabones 1, 2, 5 y 6. Se señalan también los vectores posición de cada eslabón en este sub circuito y las coordenadas generalizadas involucradas. Se trata de un sub circuito de cuatro barras que tiene al eslabón 1 como bastidor, al eslabón 2 como manivela, al eslabón 5 como biela y al eslabón 6 como balancín.

El ángulo β₁ en el bastidor 1 es un parámetro geométrico ajustable en este sub circuito. Este ángulo puede hacerse variar mediante el giro manual en torno del punto E del brazo l₁, el cual está conectado a un sector circular dentado movido por una rueda dentada más pequeña. Cuando se hace girar el sector circular, el pivote D en el bastidor se reposiciona a una nueva posición, y por tanto las coordenadas (a₃,b₃) medidas respecto al sistema Axy cambian. Esto se indica esquemáticamente en la Figura 5 mediante el camino circular de centro E y de radio l₁. Una vez que se ajusta el ángulo β₁ en el bastidor, este ángulo y el pivote D permanecen fijos durante el funcionamiento del rastrillo. Por otra parte, la longitud l₅ es otro parámetro geométrico ajustable en este sub circuito, puesto que su valor puede ser ligeramente acortado o alargado en U, respecto a su valor nominal de diseño.

2.1.1.1 Ángulo de salida φ61

Se desea hallar los ángulos de salida φ₅ y φ₆₁ en función del ángulo de entrada φ₂₁. Para ello se muestra en (3) la ecuación de lazo vectorial cerrado [8]del sub circuito 1.

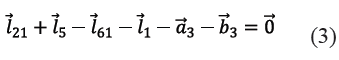
Las componentes x y y de la ecuación de lazo vectorial cerrado (3) generan las ecuaciones (4) y (5) de las que se obtendrán las coordenadas generalizadas dependientes φ₅ y φ₆₁ a partir de φ₂₁ y del valor de cada parámetro geométrico.

l₂₁ cos φ₂₁ + l₅ cos φ₅ -l₆₁ cos φ₆₁ - l₁ cos β₁ - a₃ = 0  (4)

l₂₁ sen φ₂₁ + l₅ sen φ₅ -l₆₁ sen φ₆₁ - l₁ sen β₁ - b₃ = 0    (5)

Para hallar el ángulo de salida φ₆₁ en función del ángulo de entrada φ₂₁ se reescriben las ecuaciones (4) y (5) como se muestra en las ecuaciones (6) y (7).

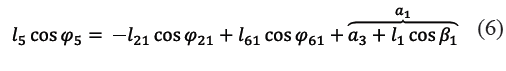
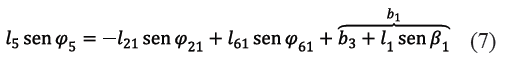
Las coordenadas (a₁,b₁) de ubicación del pivote D respecto al sistema de referencia Axy se obtienen a partir de las coordenadas (a₃,b₃) respecto de Axy del punto E, del radio l₁ y del parámetro geométrico ajustable β₁ en el bastidor, como se indica en las ecuaciones (8) y (9). Es de hacer notar que las coordenadas (a₃,b₃) tienen signo positivo o negativo según su ubicación respecto de Axy.

a₁= a₃ + l₁ cos β₁     (8)

b₁= b₃ + l₁ cos β₁     (9)

Sustituyendo (8) y (9) en (6) y (7) y elevando al cuadrado ambos miembros de las dos ecuaciones resultantes, se obtienen las ecuaciones (10) y (11).

(l₅ cos φ₅)²= (a₁- l₂₁ cos φ₂₁ + l₆₁ cos φ₆₁)²      (10)

(l₅ sen φ₅)²= (b₁- l₂₁ sen φ₂₁ + l₆₁ sen φ₆₁)²      (11)

Sumando (10) y (11), se elimina la coordenada generalizada de salida φ₅, quedando la ecuación (12).

l₅² = a₁² + b₁² + l₂₁² + l₆₁² - 2 l₂₁l₆₁ [cos φ₂₁ cos φ₆₁ + sen φ₂₁ + sen φ₆₁] - 2a₁ l₂₁ cos φ₂₁ + 2a₁l₆₁ cos φ₆₁ - 2b₁l₂₁sen φ₂₁ + 2b₁l₆₁sen φ₆₁    (12)

Dividiendo todos los términos de (12) entre el factor 2l₂₁ l₆₁ y definiendo las constantes k₁,k₂,k₃,k₄ y k₅ como se indica en las ecuaciones (13), (14), (15), (16) y (17), la ecuación (12) se puede reescribir como se indica en (18).

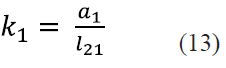
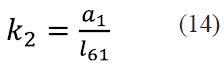
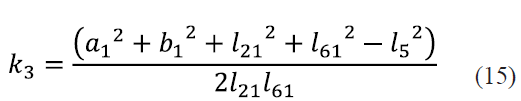
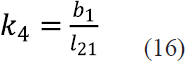
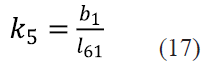
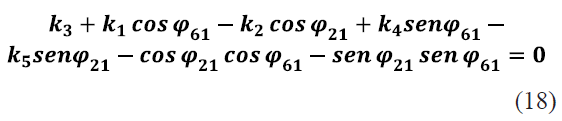
Para poder despejar φ₆₁ en (18) se introducen las identidades trigonométricas (19) y (20) y se obtiene (21).

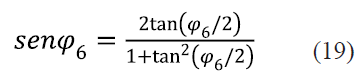
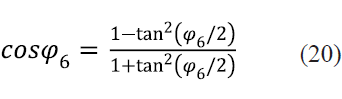
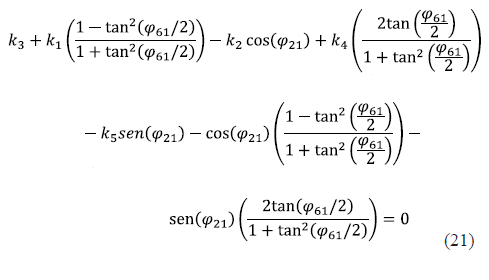
Es de hacer notar que siempre se cumple que Se puede eliminar este término del denominador de (21), con lo cual se llega a (22).

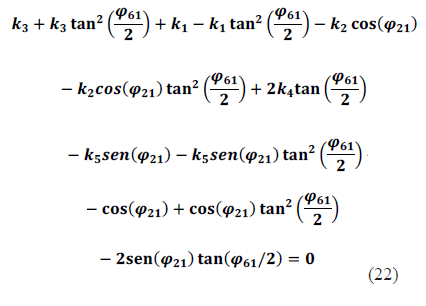
Agrupando términos semejantes en (22), se obtiene una ecuación cuadrática en tan como se indica en (23).

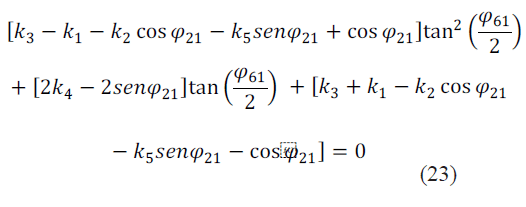
Aunque los términos k₁, k₂, k₃, k₄ y k₅ son constantes, los coeficientes de la ecuación cuadrática (23) son variables porque dependen de la posición angular de entrada φ₂₁. Si los coeficientes variables de (23) se denotan como se señala en (24), (25) y (26) se llega a la ecuación cuadrática compacta final dada en (27).

k_a = k₃ - k₁- k₂cos φ₂₁ - k₅sen φ₂₁ + cos φ₂₁    (24)

k_b =  2k₄ - 2senφ₂₁   (25)

k_c = k₃ + k₁ - k₂cos φ₂₁ - k₅sen φ₂₁ - cos φ₂₁ (26)

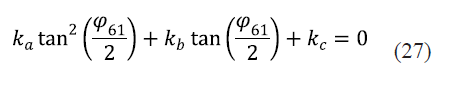
La solución de (27) para el ángulo φ_{_61} buscado es entonces (28).

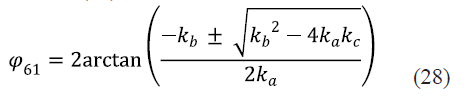
La ecuación (28) tiene dos soluciones reales o dos imaginarias según el signo del discriminante. Sin embargo, ya que en el mecanismo de rastrillo de Dorr- Oliver, el ángulo φ₂₁ de la manivela de entrada 2 varía entre 0° y 360°, la solución de (27) siempre será real. Por otra parte, por observación directa del mecanismo, la coordenada generalizada φ₆₁ está siempre en el primer cuadrante, cuando se mide este ángulo en D, en el sentido antihorario y respecto a la referencia positiva del eje x allí trazado. Se puede saber entonces cuál de los dos signos ± usar antes de la raíz en el argumento de la ecuación (28) suponiendo un signo cualquiera y observando si el sub circuito 1 adopta o no en la realidad las configuraciones resultantes que se derivan en consecuencia del signo seleccionado. En el caso de la ecuación (27) hay que adoptar el signo negativo.

2.1.1.2 Ángulo de salida φ5

Obtenido φ₆₁ de (28) ya se puede introducir éste en (6) o (7) para deducir φ₅. Sin embargo, para despejar φ₅ se usará aquí el mismo procedimiento que se empleó para obtener el ángulo de salida φ₆₁ en función del ángulo de entrada φ₂₁. Es decir, se separarán las ecuaciones (6) y (7) como se indica en (29) y (30) y se seguirán los mismos pasos que los realizados entre (8) y (28). El resultado final se muestra en (31).

l₆₁ cos φ₆₁ = -a₁ + l₂₁ cos φ₂₁ + l₅ cos φ₅ (29)

l₆₁ sen φ₆₁ = -b₁ + l₂₁ sen φ₂₁ + l₅ sen φ₅   (30)

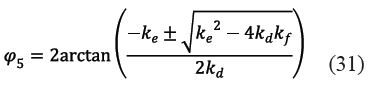
En este caso, de acuerdo a la observación directa del mecanismo real, el signo que en (31) satisface las posiciones angulares que adopta el eslabón 5 respecto al eje x positivo, es el signo positivo. Por otra parte, los términos variables k_d, k_e, k_f vienen dados por (32), (33) y (34).

k_d = k₈ + k₆ - k₇ cos φ_{21 -} k₁₀ sen φ₂₁ - cos φ₂₁     (32)

k_e = -2k₉ + 2senφ₂₁      (33)

k_f = k₈ + k₆ - k₇ cos φ_{21 -} k₁₀ sen φ₂₁ - cos φ₂₁    (34)

Y siendo k₆, k₇, k₈, k₉ y k₁₀ las constantes indicadas en (35), (36), (37), (38) y (39).

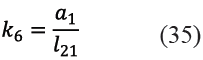
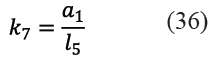
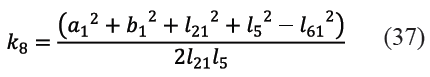
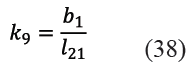
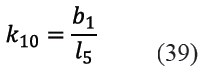
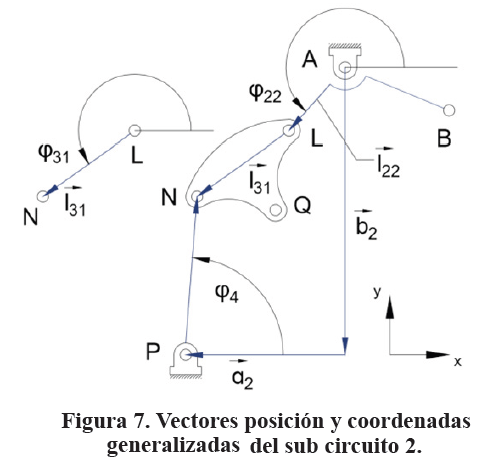
2.1.2 Sub circuito cinemático 2

El sub circuito cinemático arbitrariamente definido como sub circuito 2, mostrado en la Figura 7, está conformado por los eslabones 1, 2 3 y 4. Se trata, al igual que el sub circuito 1, de un sub circuito de cuatro barras que tiene al eslabón 1 como bastidor, al eslabón 2 como manivela, al eslabón 5 como biela y al eslabón 6 como balancín.

No hay parámetros geométricos ajustables en este sub-circuito. Los vectores posición de cada eslabón y las respectivas coordenadas generalizadas también se muestran en la Figura 7. El sistema de referencia está en Axy.

2.1.2.1 Ángulos de salida φ₄ y φ₃₁

Puesto que se trata de un sub circuito de cuatro barras, se procede de las misma manera que en el sub circuito 1, con lo cual se obtiene las ecuaciones (40) y (41) que dan cuenta de cómo varía el ángulo φ₃₁ en el eslabón 3 y el ángulo φ₄ en el eslabón 4, en función de los parámetros geométricos del sub circuito 2 y del ángulo de entrada φ₂₂ en el eslabón 2. Los signos que se deben usar son el positivo tanto en (40) como en (41) para que los resultados concuerden con los ángulos φ₄ y φ₃₁ que adopta el mecanismo real.

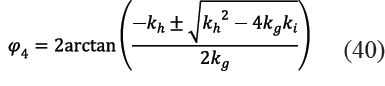
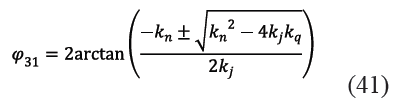
Es de hacer notar que, dada la geometría constructiva del eslabón 2 de entrada, los dos vectores , ambos definidos sobre el eslabón 2, son siempre perpendiculares entre sí, por lo que se cumple la ecuación (42).

 j₂₂ =  j₂₁ - 90°       (42)

Los términos variables k_g, k_h, k_i, k_j, k_n, k_q que aparecen en (40) y (41) vienen dados ahora por (43), (44), (45), (46), (47) y (48).

k_g = k₁₃ + k₁₁ - k₁₂ cos φ_{22 -} k₁₅ sen φ₂₂ - cos φ₂₂     (43)

k_h = -2k₁₄ + 2senφ₂₂      (44)

k_i = k₁₃ + k₁₁ - k₁₂ cos φ_{22 -} k₁₅ sen φ₂₂ - cos φ₂₂     (45)

kj = k₁₈ + k₁₆ - k₁₇ cos φ_{22 -} k₂₀ sen φ₂₂ - cos φ₂₂     (46)

k_n = -2k₁₉ + 2sen φ₂₂      (47)

k_q = k₁₈ + k₁₆ - k₁₇ cos φ_{22 -} k₂₀ sen φ₂₂ - cos φ₂₂     (47)

A su vez los términos k₁₁ a k₂₀ son los indicados de (49) a (58).

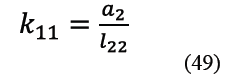
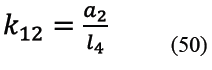
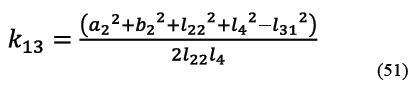
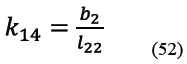
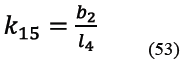
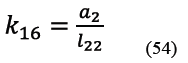
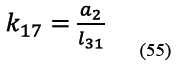
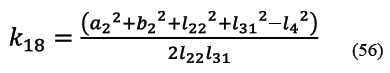
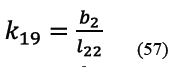
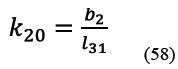
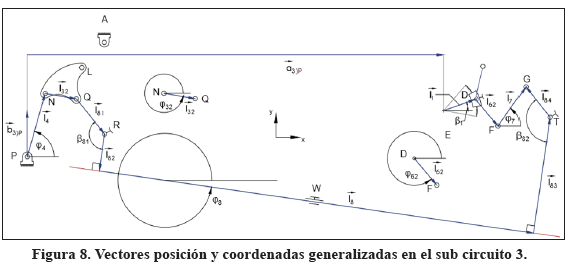
2.1.3 Sub circuito cinemático 3

Este sub circuito es más complejo que los dos anteriores pues está constituido por seis eslabones en lugar de cuatro. Éstos son los eslabones 1,4, 3, 8, 7 y 6. Sin embargo, en este sub circuito sólo se desconocen dos coordenadas generalizadas, las cuales son φ₇ y φ₈ ya que φ₆₁, φ₅, φ₄ y φ₃₁ fueron determinadas en (28), (31), (40) y (41) respectivamente. Por simplicidad, se fijará un sistema local de referencia en Pxy respecto al cual se conoce la ubicación del centro E en el bastidor. Como el rastrillo 8 está prácticamente en traslación curvilínea pura, se espera que el resultado de la gráfica de φ₈ en función de φ₂ sea prácticamente una constante.

De la Figura 8, la ecuación de lazo vectorial cerrado que se obtiene al sumar vectorialmente todos los vectores involucrados en el subcircuito 3, partiendo y llegando de nuevo a P, en un recorrido horario, viene dada por (59).

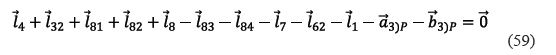
En (59) los vectores respecto del pivote fijo P están dados por (60) y (61), obtenidos de la geometría real del mecanismo. Estos vectores no deben confundirse con los vectores medidos respecto del pivote A.

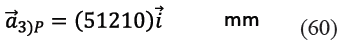
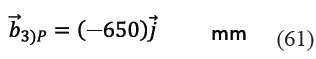
Descomponiendo (59) en sus componentes x e y respectivamente, resultan las dos ecuaciones escalares (62) y (63).

l₄ cos φ₄ + l₃₁ cosφ₃₂  + l₈₁ cos φ₈₁ + l₈₂ cos φ₈₂ + l₈ cos φ₈  - l₈₃ cos φ₈₃ - l₈₄ cos φ₈₄  - l₇ cos φ₇  - l₆₂ cos φ₆₂ - l₁ cosβ₁ - a_3)P = 0  (62)

l₄ sen φ₄ + l₃₁ sen φ₃₂  + l₈₁ sen φ₈₁ + l₈₂ sen φ₈₂ + l₈ sen φ₈  - l₈₃ sen φ₈₃ - l₈₄ sen φ₈₄  - l₇ sen φ₇  - l₆₂ sen φ₆₂ - l₁sen β₁ - a_3)P = 0  (63)

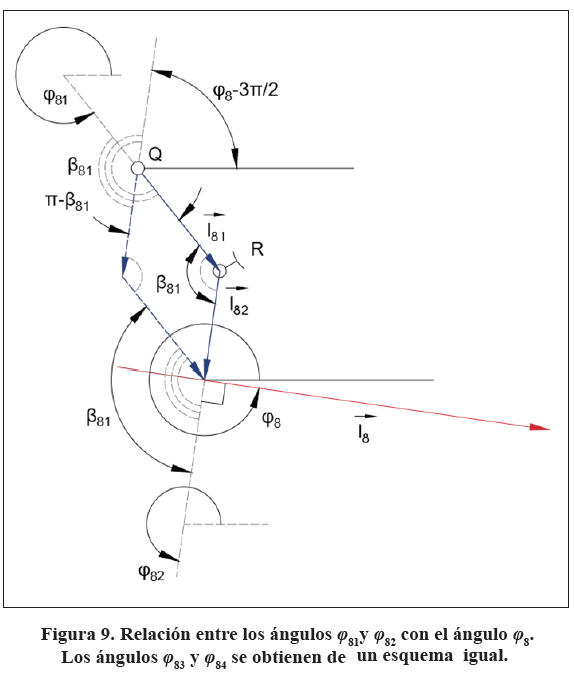
Todos los ángulos φ₈₁, φ₈₂, φ₈₃ y φ₈₄ en (62) y (63) son medidos sobre el rastrillo 8 y por tanto todos están relacionados con el ángulo φ₈. La Figura 9 y las ecuaciones (64), (65), (66) y (67) permite encontrar esas relaciones. Resulta importante resaltar que los vectores y son, por construcción propia del mecanismo, perpendiculares al vector como se indica en la Figura 8, por lo que se cumple la ecuación (65). A su vez, dada la geometría constructiva del rastrillo, los vectores son siempre paralelos entre sí, por lo que se satisface la igualdad indicada en (66).

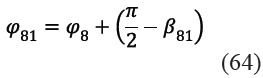
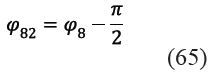
φ₈₃  =  φ₈₂       (66)

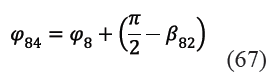
Por otra parte, los ángulos φ₃₂ y φ₆₂ que aparecen en (62) y (63) se determinan en (68) y (69) a partir de los parámetros geométricos β₃ y β₆ y de los ángulos ya conocidos φ₃₁ y φ₆₁, hallados en (41) y (28) respectivamente.

2.1.3.1 Ángulo de salida φ8

Reemplazando (64), (65), (66) y (67) en (62) y (63) y reagrupando en términos de senφ₈ y cosφ8 se obtienen las ecuaciones (70) y (71).

l₇ cos φ₇ +( l₈₂ -l₈₃  - l₈₁ cos β₈₁ + l₈₄ cos β₈₂ ) sen φ₈  +(l₈ + l₈₁sen β₈₁ - l₈₄ sen β₈₂) cos φ₈ + [l₄ cos φ₄ + l₃₂ cos φ₃₂ - l₆₂ cosφ₆₂ - l₁ cos β₁  - a_3)P ] = 0       (70)

l₇ senφ₇ +( l₈₂ -l₈₃  - l₈₁ senβ₈₁ + l₈₄ senβ₈₂ ) sen φ₈  +(l₈ + l₈₁ cos β₈₁ - l₈₄ cos β₈₂) cos φ₈ + [l₄ senφ₄ + l₃₂ senφ₃₂ - l₆₂ senφ₆₂ - l₁ senβ₁  - b_3)P ] = 0       (71)

En (70) y (71) es necesario despejar las incógnitas φ₇ y φ₈ que aparecen en los argumentos de las funciones seno y coseno. Ya se conocen de (40), (68) y (69) las coordenadas generalizadas de salida φ₄, φ₃₂ y φ₆₂ en función de la coordenada generalizada de entrada φ₂₁ y de los parámetros geométricos del mecanismo. Con el propósito de despejar φ₇ y φ₈ se asignará a las variables k₂₁ y k₂₂ indicadas en (72) y (73) el valor de la suma de todos los términos que son independientes de las incógnitas φ₇ y φ₈. Estos términos son los reflejados entre corchetes en (70) y (71). También se asignará a las variables k₂₃ y k₂₄ indicadas en (74) y (75) el valor respectivo de la suma de los términos entre paréntesis que multiplican a los términos senφ₈ y cosφ₈ en dichas ecuaciones (70) y (71).

k₂₁ = [l₄ cos φ₄ + l₃₂ cos φ₃₂ - l₆₂ cos φ₆₂ - l₁ cos β₁  - a_3)P ]       (72)

k₂₂ = [l₄ sen φ₄ + l₃₂ sen φ₃₂ - l₆₂ sen φ₆₂ - l₁ sen β₁  - b_3)P ]         (73)

k₂₃ = (l₈₂ -l₈₃ - l₈₁cosβ₈₁ + l₈₄cosβ₈₂)      (74)

k₂₄ = (l₈ + l₈₁senβ₈₁ - l₈₄senβ₈₂)      (75)

Sustituyendo (72), (73), (74) y (75) en (70) y (71) quedan las ecuaciones (76) y (77).

- l₇ cos φ₇ + k₂₃senφ₈₁ + k₂₄cosφ₈ + k₂₁ = 0       (76)

- l₇ sen φ₇ + k₂₄sen φ₈ - k₂₃cos φ₈ + k₂₂ = 0         (77)

Separando términos en (76) y (77) se llega a (78) y (79).

l₇ cos φ₇ = k₂₃sen φ₈ + k₂₄cos φ₈ + k₂₁        (78)

l₇ cos φ₇ = k₂₄sen φ₈ + k₂₃cos φ₈ + k₂₂        (79)

Elevando al cuadrado cada una de las ecuaciones (78) y (79) y sumándolas se consigue (80).

l₇² = ( k₂₃sen φ₈ + k₂₄cos φ₈ + k₂₁ )² + (k₂₄sen φ₈ - k₂₃cos φ₈ + k₂₂)²         (80)

Desarrollando los cuadrados en (80) y factorizando queda (81).

0 = 2 (k₂₁ k₂₃+ k₂₂ k₂₄ )senφ₈ + 2 (k₂₁ k₂₄ - k₂₂ k₂₃) cosφ₈ +  (k₂₁² + k₂₂²  + k₂₃² + k₂₄² -  l₇² )     (81)

Si los distintos términos entre paréntesis de (81) se agrupan en las variables k₂₅, k₂₆ y k₂₇ indicados en (82), (83) y (84) se llega a (85).

k₂₅ = 2(k₂₁ k₂₃+ k₂₂ k₂₄ )     (82)

k₂₆ = 2(k₂₁ k₂₄ - k₂₂ k₂₁ )     (83)

k₂₇ = 2(k₂₁² + k₂₂²  + k₂₃² + k₂₄² -  l₇² )    (84)

0 =  k₂₅sen φ₈ + k₂₆cos φ₈ + k₂₇    (85)

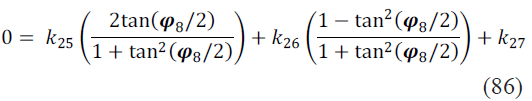
Desarrollando (86) se consigue (87)

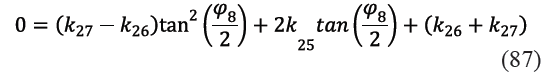
Si se definen las variables k_w, k_x y k_z indicadas en (88), (89) y (90) y se usan en (87) se puede escribir (91)

k_w = (k₂₇ - k₂₆)     (88)

k_x = 2k₂₅              (89)

k_z = (k₂₆ + k₂₇)     (90)

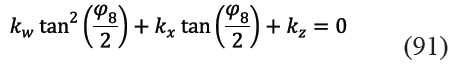
La solución de (91) se muestra en (92).

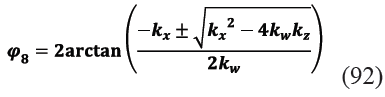
Al igual que en los dos sub circuitos anteriores, (91) es una ecuación cuadrática en tangente del ángulo mitad de φ₈ con dos posibles soluciones para esta coordenada generalizada de salida. El valor correcto del signo a tomar antes de la raíz cuadrada del discriminante en (92) será aquél que se corresponda con lo que ocurre en la práctica. En este caso, se puede comprobar que el signo correcto es el positivo, puesto que se sabe, por mediciones prácticas, que el ángulo φ₈ sobre el elemento 8 es casi constante durante todo el recorrido e igual a -9º, valor éste ligeramente menor al ángulo de -10º de inclinación de la cuba, todo lo cual coincide con los resultados reflejados en los resultados este trabajo.

2.1.3.2 Ángulo de salida φ₇

Para hallar la expresión que relaciona el ángulo φ₇ con la coordenada generalizada de entrada, se puede despejar φ7 en cualquiera de las ecuaciones (78) o (79). Sin embargo, como el objetivo de éste trabajo es hallar la trayectoria del punto extremo O del rastrillo en la descarga, y como para ello ya es suficiente con hallar φ₃₁, φ₄, φ₅, φ₆₁ y φ₈ , tal como se deduce de (93), no se mostrará éste resultado.

2.2 TRAYECTORIA DEL PUNTO O

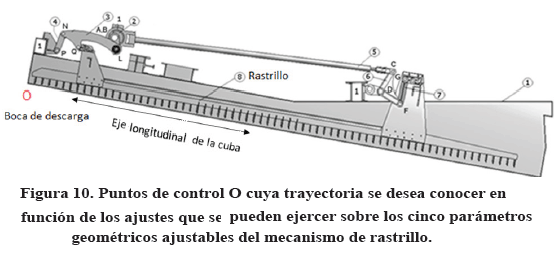
Habiéndose obtenido la relación existente entre las seis coordenadas generalizadas de salida, los veintisiete parámetros geométricos, y la coordenada generalizada de entrada del rastrillo desarenador se puede proceder a graficar la trayectoria [9] de cualquier punto en el mecanismo. Por ser de especial interés para el control del barrido, se seleccionará para tal propósito el punto O mostrado en la Figura 10, ubicado en el extremo de descarga del rastrillo.

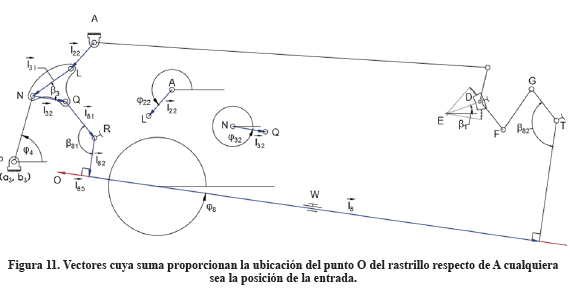
Para conocer la trayectoria de O se requiere tener una expresión que permita ubicar en todo momento la posición del extremo de descarga del rastrillo respecto a un punto en el bastidor. Para ello se introduce el vector medido desde el sistema Axy ubicado en el pivote A. La trayectoria de O vendrá dada por la gráfica de la ecuación que define la posición para todo tiempo de la cabeza del vector , la cual a su vez es una función exclusiva de la posición angular particular que adopte el elemento de entrada. El vector es igual a la suma vectorial indicada en (93) obtenida de acuerdo con la Figura 11. Todos los vectores que participan en esta suma son ahora conocidos.

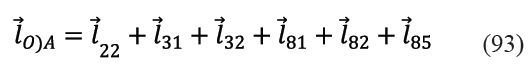
partir de (93) la trayectoria del punto O en el rastrillo, medida respecto al bastidor en A, vendrá dada por la ubicación en el plano de todos los puntos por los que pasa la cabeza del vector indicado en (94). El vector se mide a partir del extremo final del vector . La longitud del vector así medido es de 740 mm.

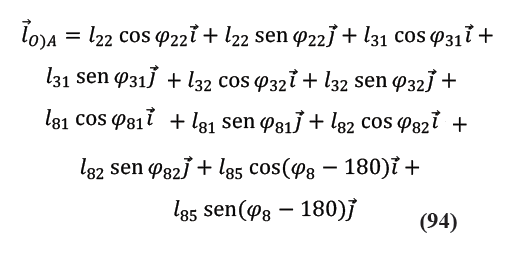
3. RESULTADOS Y DISCUSIÓN

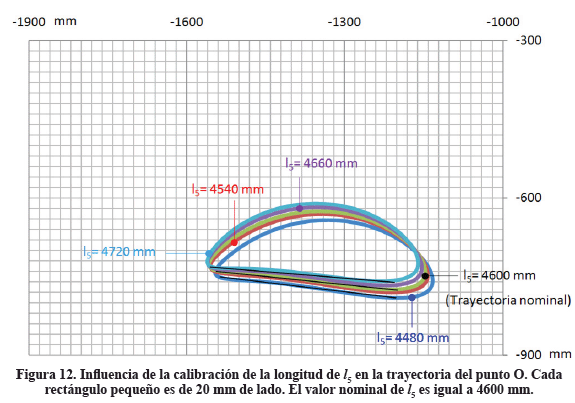
3.1 Trayectoria de O en función de la calibración de l₅

La figura 12 muestra la influencia de la calibración de l₅ sobre la trayectoria de barrido que describe el punto O del rastrillo en la descarga.

Las trayectorias obtenidas son las que se observarían al mirar el mecanismo desde el lado del motor. La luz nominal medida sobre el mecanismo, entre el borde del diente del rastrillo en la descarga y el fondo de la cuba para los valores nominales de los parámetros geométricos, es de 20 mm. Se entiende por luz nominal, la que se tiene cuando todos los parámetros geométricos de calibración se encuentran en sus valores nominales mostrados en la tabla I del anexo.

Se realizan cinco gráficas. Una es la trayectoria nominal, dibujada en verde en todas las figuras que siguen y las otras cuatro son las trayectorias cuando la dimensión nominal del parámetro geométrico l₅ aumenta o disminuye. Dos serán las trayectorias cuando el valor de l₅ esté por encima del nominal y dos cuando esté por debajo.

En este caso, la trayectoria nominal en la figura 12, es aquella que se obtiene cuando la longitud del brazo de conexión l₅ es de l₅ = 4600 mm. A partir de este valor central, se aumenta o disminuye para el análisis la magnitud de l₅ en pasos de ±60 mm hasta llegar a l₅=4720 mm y a l₅=4480 mm respectivamente, que son los topes superior e inferior que se pueden alcanzar al actuar sobre l5.

Se observa que O tiene una carrera de avance hacia la izquierda para barrer y una de retroceso a la derecha para reposicionarse.

A pesar de que al cambiar la longitud de l₅, las curvas de entrada que hace el punto O al inicio del barrido son complejas y diferentes, las carreras de avance son principalmente segmentos casi rectos y casi paralelos, como se resalta en la Figura 12. Estos segmentos tienen una inclinación de unos -7º respecto a la horizontal positiva y sus longitudes son prácticamente iguales, ubicándose en el entorno de los 360 mm de largo en todos los casos.

En la carrera de retroceso, y al variar la longitud de l₅ en el rango indicado, el punto O del rastrillo asciende unos 160 mm en cada caso.

De acuerdo con los resultados obtenidos, un incremento de 120 mm en la longitud de l₅ respecto al valor nominal de este parámetro aleja al punto O unos 12 mm del fondo de la cuba. Por el contrario, una disminución en la longitud de l₅ de 120 mm respecto al valor nominal de este parámetro, acerca al punto O unos 12 mm al fondo de la cuba. Este acercamiento de 12 mm al fondo de la cuba, no puede producir un choque con ésta, toda vez que la luz nominal original es de 20 mm.

Por otra parte, cuando se incrementa en 120 mm el valor nominal de l₅, se produce un ligero corrimiento de unos 7 mm de la trayectoria del punto O hacia la izquierda de la boca de descarga, y cuando se disminuye el valor de l₅ en 120 mm, se produce un corrimiento de la trayectoria del punto O a la derecha, también de unos 7 mm. De esta manera, para todo propósito práctico, se concluye que la calibración de l₅ sirve para hacer un ajuste fino de la distancia a la que el punto O pasa respecto al fondo de la cuba, no siendo significativa su influencia en el alejamiento o acercamiento de O a la boca de descarga en la dirección longitudinal de la cuba, cuando se comparan estos pequeños valores relativos con la larga dimensión de 7500 mm de la cuba.

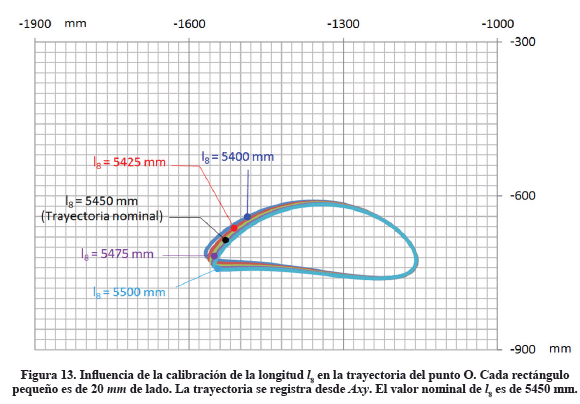
3.2 Trayectoria de O en función de la calibración de l₈

La figura 13 muestra la influencia de la calibración de l8 sobre la trayectoria de barrido que describe el punto O del rastrillo.

Se realizan las gráficas a partir del valor nominal de calibración l₈ =5450 mm, aumentando o disminuyendo este valor para el análisis de la respuesta, en pasos de ±25 mm hasta llegar a l₈ =5500 mm y a l₈ =5400 mm respectivamente, que son los topes superior e inferior que se consiguen al actuar sobre l₈.

En este caso, al calibrarse la longitud l₈, se obtiene que las carreras de barrido son segmentos casi rectos, pero no paralelos. Sin embargo, las longitudes de estas carreras son prácticamente iguales en todos los casos, siendo éstas, de unos 360 mm de largo. En la carrera de retroceso, al variar la longitud de l₈ en el rango indicado, el punto O del rastrillo asciende por igual unos 155 mm en todos los casos.

Para estos juegos de valores de l₈, el ligero corrimiento de la trayectoria del punto O hacia la izquierda o la derecha de la boca de descarga a lo largo del eje longitudinal de la cuba, es de unos 16 y 8 mm respectivamente, lo que no es significativo en comparación con la dimensión longitudinal de 7500 mm de la cuba.

De acuerdo con los resultados obtenidos, se puede señalar que un incremento de 50 mm en la longitud de l₈ respecto al valor nominal de este parámetro, el punto O, unos 8 mm al fondo de la cuba. Este acercamiento de 8 mm al fondo de la cuba, no puede producir un choque con ésta, toda vez que la luz nominal original es de 20 mm. Por el contrario, una disminución en la longitud de l₈ de 50 mm respecto al valor nominal de este parámetro, aleja al punto O unos 16 mm del fondo de la cuba. Al calibrarse la longitud de l₈, las variaciones en la trayectoria de O se concentran solo al final de los recorridos de barrido por lo que se llega así a la conclusión de que un aumento en la longitud de l₈, manteniendo el resto de parámetros calibrables en sus valores nominales, es beneficioso para un mejor raspado de los sedimentos en la propia boca de descarga. Del mismo modo, si se disminuye la longitud de l₈ se genera una trayectoria más paralela al eje longitudinal de la cuba y si se aumenta la longitud de l8, entonces la trayectoria se hace más horizontal.

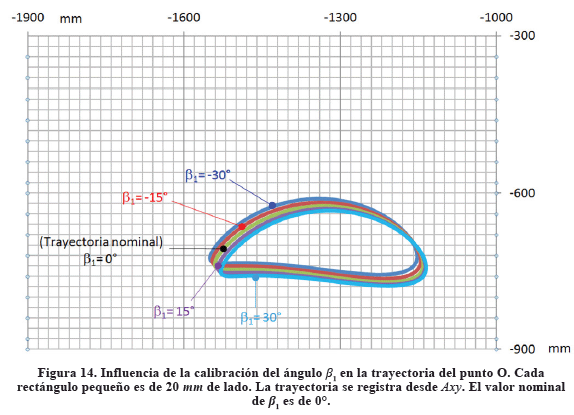
3.3 Trayectoria de O en función de la calibración de β₁

La figura 14 muestra la influencia de la calibración de β₁ sobre la trayectoria de barrido que describe el punto de descarga O. Se realizan las gráficas a partir del valor nominal de diseño de β₁=0°, con pasos para el análisis de ±15º hasta llegar a β₁=30° y β₁=-30° respectivamente, que son los topes superior e inferior de β₁ a los que se puede arribar en este mecanismo. Al igual que en las Figuras 12 y 13, las carreras de barrido son prácticamente segmentos de recta, de unos 360 mm de largo en todos los casos.

Se observa que al ajustar el ángulo β₁, las modificaciones de la trayectoria de O no son significativas entre sí en la dirección longitudinal de la cuba, pero sí lo son en la dirección de acercamiento a alejamiento al fondo de ésta. Un incremento de 30º por encima del ángulo nominal de β₁ hace que el punto O se acerque al fondo de la cuba, bajando su trayectoria en unos 12 mm respecto a la trayectoria que se registra para el valor nominal de β₁=0°. Una disminución de 30º del ángulo β₁ hace que el punto O se aleje del fondo de la cuba, unos 20 mm. Se concluye entonces que sólo para grandes cambios relativos en el ajuste del ángulo β₁ es que éste juega un papel significativo en el control del barrido que hace el punto O del rastrillo. Los ajustes en el ángulo β₁ producen entonces, al igual que lo hace el ajuste de l₈, un ajuste fino de la luz entre el rastrillo y la cuba. El diseñador original ha dispuesto sobre el eslabonamiento, de un mecanismo de ruedas dentadas para ajustar fácilmente éste ángulo, lo que hace que éste sea el ajuste más fácil de practicar.

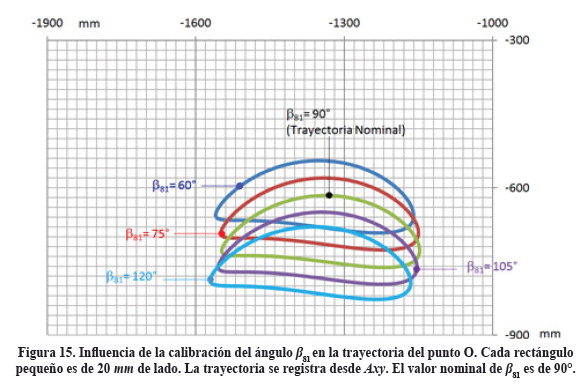
3.4 Trayectoria de O en función de la calibración de β₈₁

La figura 15 muestra la influencia de la calibración de β₈₁ sobre la trayectoria de barrido que describe el punto de descarga O. En este caso, la trayectoria nominal de O es la que se registra cuando β₈₁=90°. A partir de este valor nominal se aumenta o disminuye para el análisis la magnitud de β₈₁ en pasos de ±15 ° hasta llegar a β₈₁=120° y a β₈₁=60° respectivamente, que son los topes superior e inferior que se pueden alcanzar al ajustar β₈₁.

Se deduce que la calibración de este parámetro induce grandes modificaciones de la altura a la que O pasa respecto al fondo de la cuba. Así, un incremento de 15º en el ángulo β₈₁, desde 90º a 105º , bajaría la trayectoria de O en 60 mm respecto a la nominal y como la luz nominal es de 20 mm, el rastrillo chocaría indebidamente contra el fondo de la cuba. Un incremento desde 90º a 120º en el ángulo β₈₁ bajaría a la trayectoria de O cerca de 78 mm más allá de lo que lo hace la trayectoria nominal. Por el contrario, una disminución del ángulo β₈₁ de 30° respecto al valor nominal, levantaría considerablemente la trayectoria en unos 80 mm, con lo cual se pierde la acción de barrido.

Se descifra así una importante característica constructiva del funcionamiento de este mecanismo de rastrillo, concluyéndose que la calibración de éste ángulo ha sido dispuesta por el diseñador original para tener un control relativo grande de la profundidad o de la altura de la trayectoria de O respecto a la cuba, con el fin de poder utilizar éste tipo de clasificador en otras aplicaciones distintas a las que se llevan a cabo en este proceso particular de recuperación de sedimentos en el proceso Bayer de la empresa Bauxilum. Se determina así que para este proceso en particular, el ángulo β₈₁ no debe ser usado para calibrar la luz que deja la trayectoria de barrido del punto O.

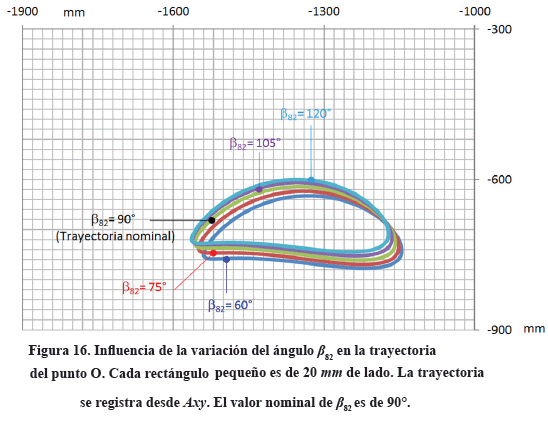
3.5 Trayectoria de O en función de la calibración de β₈₂

La figura 16 muestra la influencia de la calibración de β₈₂ sobre la trayectoria de barrido que describe el punto de descarga O. Se realizan las gráficas para el valor nominal de β₈₂=90°, aumentando 20° a partir de allí hasta llegar a β₈₂=130°. También se disminuye al ángulo nominal hasta llegar a β₈₂=50°.

La respuesta es similar a las obtenidas en las Figuras 12 y 14 cuando se calibra l₅ y β₁, Sin embargo, difiere notablemente de lo que ocurre con la trayectoria de O al calibrar β₈₁ pues en ésta caso, además de que las modificaciones de la trayectoria de O son mucho menores, la respuesta es opuesta a lo que ocurre con β₈₁, ya que ahora una disminución del ángulo β₈₂ de 40° respecto al ángulo nominal, acerca el punto O unos 20 mm hacia el fondo de la cuba y un aumento de 40° levanta la trayectoria unos 8 mm.

De esta manera se concluye que la calibración del ángulo β₈₂ también sirve para realizar un ajuste fino de la trayectoria de O respecto al fondo de la cuba.

3.6 Trayectoria de O ante la manipulación conjunta de los cinco parámetros geométricos.

Las gráficas de las figuras 12 a 16 muestran cómo cambian las trayectorias del punto O ante la manipulación individual de sus cinco parámetros geométricos calibrables. Esto es, no se toma en cuenta en estas respuestas, la posibilidad que existe de manipular dos o más parámetros geométricos a la vez, en lugar de hacerlo sobre uno sólo. Como ya ha sido deducido, una disminución de l₅ o de β₈₂ respecto a sus valores nominales, acercaría el punto O al fondo de la cuba y un incremento de éstos, lo alejaría. Por el contrario, una disminución de los parámetros l₈, β₁ o β₈₁, alejaría la trayectoria de O del fondo de la cuba y un incremento en el valor de estos parámetros, lo acercaría.

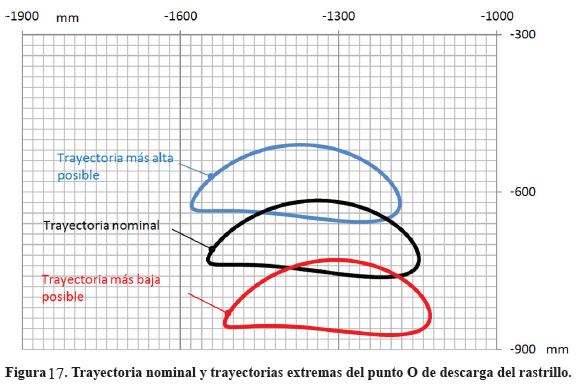
La Figura 17 muestra el resultado que se obtiene cuando los cinco parámetros geométricos ajustables del mecanismo se mueven todos simultáneamente hacia sus posiciones críticas, esto es, aquellas para las cuales la trayectoria de O es la más baja posible o aquellas para las cuales dicha trayectoria es la más alta posible. Si se hace esto, se observa que la trayectoria de O mantiene su forma básica y que el desplazamiento de la trayectoria a lo largo del eje longitudinal de la cuba se corre unos 30 mm a la izquierda o la derecha de la trayectoria nominal. Sin embargo, el punto O bajaría o subiría significativamente unos 120 mm o unos 100 mm respectivamente, respecto a la trayectoria nominal. Ambas son trayectorias no deseadas, pues el rastrillo bajaría y chocaría con el fondo de la cuba o subiría en demasía, con lo cual no barrería. Como en la empresa Bauxilum, la luz de operación del mecanismo de rastrillo es de 20 mm, es suficiente entonces con manipular uno sólo de los parámetros geométricos ajustables para modificar mediante un ajuste fino la trayectoria respecto a la nominal.

IV. CONCLUSIONES

Para ajustar las trayectorias de barrido del mecanismo de rastrillo es necesario primero colocar cada parámetro geométrico ajustable en su valor nominal de diseño, para los cuales la luz nominal mínima entre los dientes del rastrillo y el fondo de la cuba es de 20 mm.

Una disminución respecto a sus valores nominales, de los parámetros ajustables l₅ o β₈₂, sirve para hacer un ajuste fino de hasta 12 mm de acercamiento de los dientes del rastrillo al fondo de la cuba.

Un aumento respecto a sus valores nominales, de los parámetros ajustables l₅ o β₈₂, alejaría hasta 12 mm, los dientes del rastrillo, del fondo de la cuba.

Los ajustes de l₅ o β₈₂ no conducen a la posibilidad de que los dientes del rastrillo choquen con el fondo de la cuba.

Una disminución respecto a sus valores nominales, de los parámetros ajustables l₈, β₁ o β₈₁, alejaría los dientes del rastrillo del fondo de la cuba en 16 mm, 20 mm y 80 mm respectivamente.

Un aumento respecto a sus valores nominales, de los parámetros ajustables l₈, β₁ o β₈₁, acercaría los dientes del rastrillo al fondo de la cuba en 8 mm, 12 mm y 60 mm respectivamente.

Los ajustes de l₈ o β₁ no conducen a la posibilidad de que los dientes del rastrillo choquen con el fondo de la cuba.

El ajuste de β₈₁ proporciona cambios significativos en la altura a la que pasan los dientes del rastrillo respecto al fondo de la cuba, presentándose la posibilidad de que su manipulación indebida conduzca a que los dientes del rastrillo choquen contra ella.

Ningún ajuste conduce a cambios significativos en el recorrido total que hacen los dientes a lo largo del eje longitudinal de la cuba. Estos recorridos se mueven en el entorno de los 360 mm.

Para calibrar fino la luz entre el rastrillo y el fondo de la cuba se debe ajustar con preferencia el ángulo β₁.

La combinación de ajustes simultáneos de varios parámetros geométricos no es necesaria en el mecanismo de rastrillo de Bauxilum.

V. REFERENCIAS

1. Fogarasy A., and Smith M., "The case for a general method of kinematic analysis of plane mechanisms based on equations of constraint". Part C: Journal of Mechanical Engineering Science. Proc. Instn. Mech. Engrs. 209. pp. 337- 343, United Kingdom, 1995.         [ Links ]

2. Escanaverino J., Toll A., y Cárdenas T. "Dichromathic graphs: A tool for the algoritmic education of mechanical engineers". 2000 ASME design Engineering Technical Conferences and Computers Information in Engineering Conference, September 2000. Baltimore, Maryland. USA.         [ Links ]

3. Fogarasy A., Smith M. "The influence of manufacturing tolerances on the kinematic performance of mechanisms". Part C: Journal of Mechanical Engineering Science. Proc Instn Mech Engrs Vol 209. pp. 35-45. 1998.         [ Links ]

4. Mendoza J., Caraballo S., Solis D., Gómez O., "Influencia de las dilataciones térmicas en la descalibración del movimiento paralelo de las tres cuchillas de puesta a tierra de un seccionador eléctrico". Revista Universidad, Ciencia y Tecnología (on line). 2012, vol.16, n.63, pp. 125-141. ISSN 1316-4821.         [ Links ]

5. Mendoza J., and Otero L., "Calibration of the tight seal of the discharge mechanism doors on a rail wagon using adjustable members". ESDA2006- 95102, Proc. 8th Biennial Conference on Engineering Systems Design and Analysis, ASME, Turin, Italy, 2006. Pp. 323-335. ISBN: 0-7918-4250-9.         [ Links ]

6. Mendoza J., y Otero L., "Reubicación de los eslabones de calibración de las tres cuchillas de puesta a tierra de un seccionador eléctrico". X Congreso Iberoamericano de Ingeniería Mecánica, CIBEM 10, Porto, Portugal, 2011.         [ Links ]

7. Pinto L., Melo G., y Socarras C., "Mecánica Vectorial para ingenieros. Dinámica". Primera edición. Universidad de La Guajira, Riohacha, Colombia, 2016. ISBN 978-958-8942-18-6. 264 páginas.         [ Links ]

8. Norton R. "Diseño de Maquinaria. Síntesis y análisis de máquinas y mecanismos". Quinta edición. Mc Graw Hill Education. 2013. México. ISBN 978-607-15-0935-2. 601 páginas.         [ Links ]

9. Majarena A., Santolaria J., Samper D., Aguilar J., "Analysis and design improvements of a high precision kinematic mechanism". Noviembre, 2013. Revista de ingeniería Dyna. Volumen 88. Bilbao. España. Pp. 666-674.         [ Links ]

VI. NOMENCLATURA

A, B, C, D, E, H, ................O´, Q´: Pares Cinemáticos

a_i: Longitud constante en la dirección x

b_i: Longitud constante en la dirección y

l_i: Longitud del eslabón i-ésimo

p_i: Parámetro geométrico i-ésimo

q_i: i-ésima coordenada generalizada.

β_i: Ángulo constante i-ésimo.

φ_i: Orientación angular o coordenada generalizada del eslabón i-ésimo.

ANEXOS

La tabla I del anexo indica los valores nominales de los parámetros geométricos del mecanismo, entre los que se encuentran los cinco parámetros geométricos ajustables.