I. INTRODUCCIÓN

El aprendizaje en matemáticas ha significado un desafío continuo y enriquecedor para los estudiantes a lo largo del tiempo. Más allá de ser simplemente un conjunto de reglas y fórmulas, la matemática es un lenguaje universal que nos permite entender y describir patrones, estructuras y relaciones en el mundo que nos rodea. Para muchos estudiantes, el aprendizaje de las matemáticas ha representado no solo la adquisición de conocimientos específicos, sino también el desarrollo de habilidades analíticas y la capacidad de abordar problemas de manera sistemática. La resolución de problemas matemáticos implica no solo la aplicación mecánica de procedimientos, sino también la comprensión profunda de los conceptos subyacentes, lo que estimula el pensamiento crítico y la toma de decisiones informadas ¹.

La afirmación realizada por el Programme for International Student Assessment (PISA) se basa en los resultados de las últimas evaluaciones llevadas a cabo por los países participantes. Estos revelan que el 31,1% de los estudiantes no lograron alcanzar el nivel mínimo establecido. Es alarmante observar que, en los países latinoamericanos, más del 50% de los evaluados se encuentran en el nivel más bajo, subrayando una preocupante brecha en el rendimiento académico. En el caso específico de Perú, los datos son reveladores. Aproximadamente el 30,5% de los estudiantes lograron alcanzar el nivel 1, lo cual indica un nivel de competencia muy básico. Además, un inquietante 35,7% de los estudiantes se sitúa por debajo de este nivel, evidenciando una falta significativa de habilidades fundamentales en materias evaluadas por PISA ^2,3. Estas cifras resaltan la necesidad apremiante de implementar estrategias educativas que aborden las deficiencias identificadas. Es crucial adoptar enfoques pedagógicos innovadores y centrados en el estímulo de habilidades cognitivas clave. Asimismo, se requiere un análisis profundo de las estructuras educativas y la asignación de recursos para abordar las disparidades en el acceso a una educación de calidad. El impacto de estos resultados no se limita únicamente al ámbito educativo; también plantea desafíos a nivel socioeconómico, ya que la preparación académica de los estudiantes influye directamente en su capacidad para contribuir de manera efectiva al desarrollo de sus comunidades y al progreso de sus países ^3,4.

En Perú la certificación de los logros de aprendizaje en el área de matemática, informados por la Oficina de Medición de la Calidad de los aprendizajes (UMC) ² indica que en las evaluaciones estandarizadas en el nivel de secundaria a nivel nacional, el 30,3% de los escolares evaluados se encuentran en un nivel muy bajo, que revela que no alcanzó los aprendizaje de su grado y solo el 36,8% logró aprendizajes muy básicos en relación a lo que se espera para el ciclo evaluado. A nivel de región, la ciudad de Tumbes en Perú, se presentan con porcentajes por debajo del nivel nacional. Además, hay que resaltar que existen otras carencias en los estudiantes como la falta de habilidades para definir problemas matemáticos y encontrar información apropiada, lo que causa ansiedad, impaciencia y desmotivación para el manejo y lectura de textos extensos.

Gazzola y Otero ⁵ afirman que las causas se atribuyen al paradigma de enseñanza tradicional, que tienen una alta tendencia dominante, pero además se percibe el conocimiento matemático como autoevidente e incuestionable. Incluso los docentes del área de matemáticas suelen tener complicaciones para la formulación de ecuaciones apropiadas y soluciones idóneas en los problemas. De esta manera, se ha difundido una práctica docente que propone tareas y actividades con parámetros fijos, que pretende únicamente ubicar soluciones numéricas y únicas, sin motivar al pensamiento crítico, lo que conduce a un aprendizaje matemático memorístico, basado en procesos únicos e identificación de teorías clásicas ⁶. Estas situaciones previas conducen a afirmar que no se refuerza el pensamiento divergente en los estudiantes, haciendo que la comprensión matemática sea más compleja ⁷. La falta de énfasis en el pensamiento divergente en el ámbito educativo puede limitar el desarrollo de habilidades cruciales para la resolución de problemas y la creatividad en el campo de las matemáticas. De ahí que en este trabajo se ha considerado el estudio del pensamiento divergente y las formas de aplicarlos en el aula para que exista una mayor comprensión de las herramientas matemáticas en los estudiantes de secundaria.

II. DESARROLLO

El pensamiento divergente implica la capacidad de generar múltiples soluciones o enfoques a un problema dado. Al no fomentar este tipo de pensamiento en los estudiantes, se corre el riesgo de limitar su capacidad para abordar situaciones matemáticas desde diferentes perspectivas, lo que a su vez obstaculiza el desarrollo de un entendimiento profundo de los conceptos. En este sentido, la enseñanza convencional a menudo se centra en la memorización de fórmulas y la aplicación de algoritmos específicos, dejando poco espacio para la exploración de enfoques no convencionales o la búsqueda de soluciones alternativas ⁸. Esto puede resultar en estudiantes que son hábiles para aplicar métodos aprendidos, pero que carecen de la flexibilidad mental necesaria para enfrentar desafíos matemáticos complejos.

Promover el pensamiento divergente en el aula de matemáticas implica fomentar la curiosidad, la exploración y la experimentación. Se trata de alentar a los estudiantes a cuestionar, a proponer diferentes enfoques y a desarrollar su capacidad para pensar de manera creativa frente a problemas matemáticos. La inclusión de actividades que fomenten la resolución de problemas abiertos y el trabajo en grupo también puede contribuir significativamente a fortalecer el pensamiento divergente en el contexto matemático ⁹. De esta manera, se puede decir que la falta de énfasis en el pensamiento divergente en la enseñanza de las matemáticas puede representar una limitación significativa para el desarrollo integral de los estudiantes. Es imperativo que los educadores busquen estrategias pedagógicas que promuevan la diversidad de enfoques y soluciones, proporcionando así a los estudiantes las herramientas necesarias para enfrentar los desafíos matemáticos de manera más creativa y efectiva.

B. Teoría de Guilford

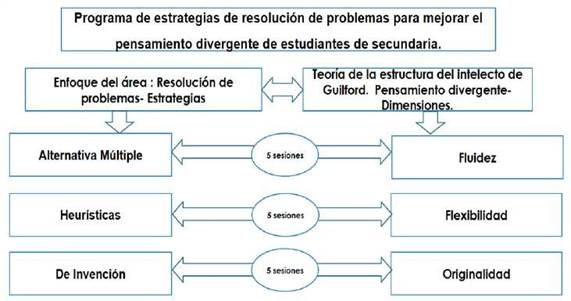
La Teoría de Guilford, es un enfoque importante en la psicología cognitiva que se centra en la estructura del intelecto humano. Guilford propuso un modelo tridimensional que buscaba comprender la naturaleza y la diversidad de las habilidades mentales. Este modelo, conocido como la Estructura de la Inteligencia Multifacética (Structure of Intellect, SOI), consta de tres dimensiones principales: las operaciones mentales, los contenidos y los productos ¹³.

Se aplicó una prueba objetiva a estudiantes de bachillerato para evaluar su aprendizaje del inglés en tres dimensiones: comprensión, habla y escucha. La prueba, que constaba de 22 reactivos mostrados en tabla 2, se estructuró siguiendo las normas para evaluar la adquisición de las habilidades lingüísticas. El objetivo era medir el rendimiento académico, las competencias en el idioma y el manejo del idioma, utilizando una escala valorativa de correcto e incorrecto. La prueba se aplicó a un grupo experimental y a un grupo de control para comparar los resultados.

• Operaciones Mentales: Guilford identificó 120 operaciones mentales diferentes, que incluyen habilidades como la memoria, la convergencia, la divergencia, la evaluación y la síntesis. Estas operaciones representan los procesos básicos que realiza la mente para procesar la información.

• Contenidos: Guilford propuso cinco tipos de contenidos mentales, que son las áreas específicas de conocimiento en las que se aplican las operaciones mentales. Estos incluyen la información visual, auditiva, simbólica, semántica y conductual.

• Productos: Los productos son las formas en que se manifiestan los resultados del pensamiento. Esto abarca desde respuestas verbales o escritas hasta la resolución de problemas y la toma de decisiones.

Guilford argumentó que la inteligencia es multifacética y que las pruebas tradicionales de coeficiente intelectual (CI) no capturan completamente la diversidad de las habilidades mentales. Su teoría buscaba proporcionar un marco más completo y detallado para entender la amplitud y la complejidad de la inteligencia ^14,15. Esta Teoría ha influido en el desarrollo de enfoques más contemporáneos para entender la inteligencia, destacando la importancia de considerar una amplia gama de habilidades y procesos mentales. Aunque su modelo no ha sido completamente adoptado en la corriente principal de la psicometría, ha contribuido significativamente a la comprensión de la complejidad del intelecto humano y ha influido en la evolución de las teorías sobre la inteligencia.

Figura 1 Diagrama del Programa. 

III. METODOLOGÍA

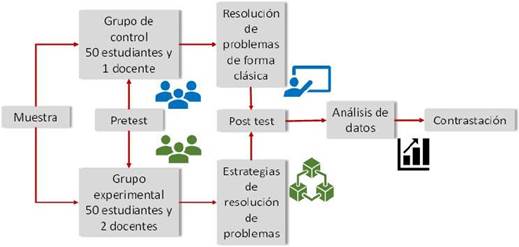
El trabajo corresponde a una investigación con enfoque cuantitativo, con diseño cuasi experimental. La población del estudio estuvo compuesta por 100 estudiantes y tres docentes de la ciudad de Tumbes en Perú, pertenecientes al primer grado de nivel secundaria. Por otro lado, la muestra fue intencionada, con un total de 50 estudiantes que conformaron el grupo de control y el experimental. Ambos grupos fueron sometidos a un pretest y un post test para poder hacer las correlaciones respectivas. Además, se aplicó una encuesta para comprobar la efectividad del programa elaborado. En la figura 2 se muestra la aplicación del programa.

Figura 2 Proceso de ejecución de la investigación Fuente: Propia 

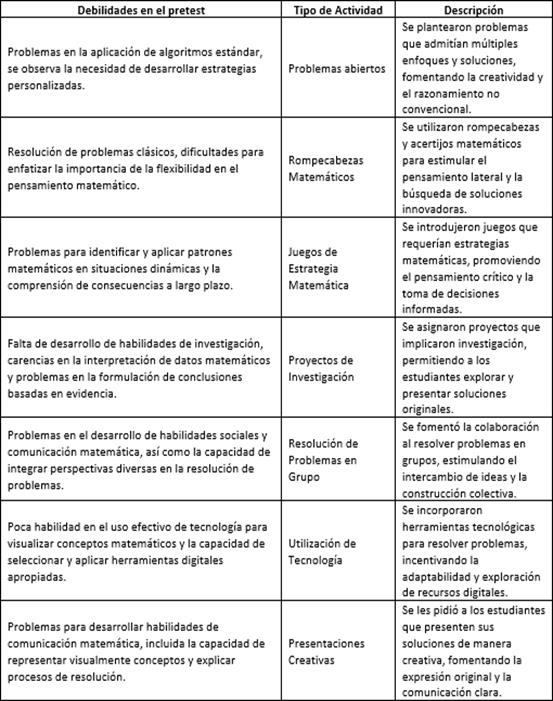
Las estrategias de resolución de problemas seleccionadas se describen en la tabla 1. Estas estrategias fueron elegidas considerando las debilidades observadas en el pretest, donde se observa que en el pretest se encontraron diversas problemáticas para que los estudiantes afrontaran los retos matemáticos con miras a un aprendizaje significativo.

Tabla 1 Debilidades encontradas en el pretest y actividades propuestas para su solución. 

Otras características relevantes del programa que se consideraron para motivar y reforzar el pensamiento divergente en la asignatura de matemáticas fueron la adaptabilidad y contextualización que son elementos fundamentales en el diseño del programa educativo. En primer lugar, se aseguró de que el programa fuera adaptable a las necesidades individuales de los estudiantes, permitiendo ajustes según sus niveles de habilidad. La diversidad en la presentación de problemas y enfoques contribuyó significativamente a fomentar la adaptabilidad del pensamiento. Además, se integraron problemas relevantes y aplicables a situaciones de la vida real, estableciendo así una conexión directa entre las habilidades matemáticas y el entorno cotidiano de los estudiantes. Por otro lado, la retroalimentación constructiva y la inclusividad fueron aspectos clave en el proceso educativo. Se proporcionó retroalimentación específica y constructiva, resaltando no solo la respuesta correcta, sino también el proceso de pensamiento empleado. Este enfoque ayudó a los estudiantes a comprender mejor su propio razonamiento. Además, se aseguró de que el programa fuera accesible para todos los estudiantes, independientemente de su nivel inicial de habilidad, mediante la diferenciación de actividades y estrategias para apoyar diversos estilos de aprendizaje. El programa no solo promovió la adaptabilidad y contextualización, sino que también se enfocó en una retroalimentación constructiva y una inclusividad que respalda la diversidad de los estudiantes. También se integraron temas y conceptos de otras disciplinas para mostrar cómo las matemáticas se entrelazan con diversas áreas del conocimiento, fomentando así la conexión de ideas y la creatividad. El programa también contó con la inclusión de reflexiones sobre el proceso de resolución de problemas, animando a los estudiantes a ser conscientes de su propio pensamiento y a desarrollar estrategias metacognitivas.

IV. RESULTADOS

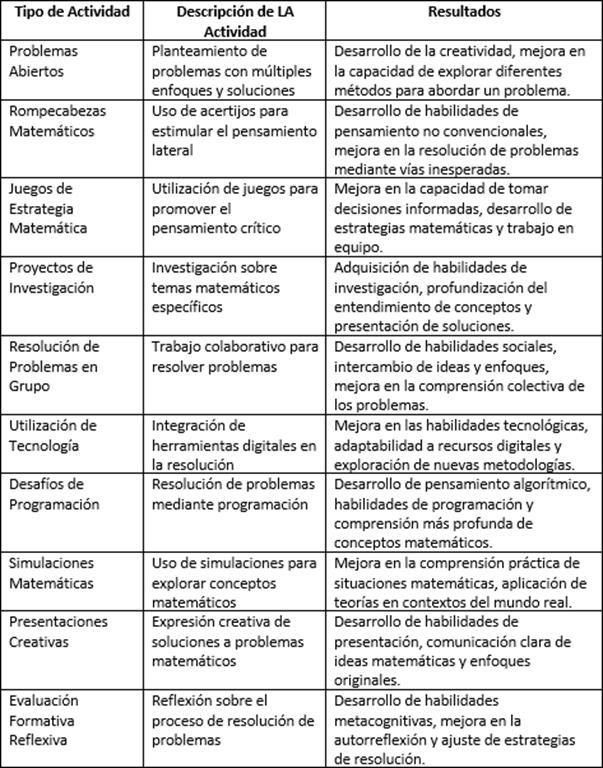
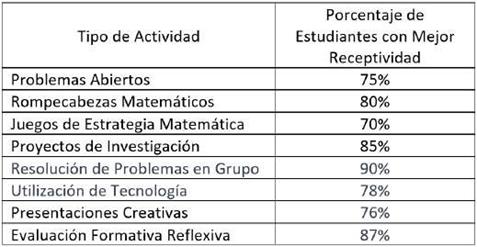
En la tabla 2 se muestran los resultados obtenidos en cada una de las actividades realizadas, y se puede apreciar que todas condujeron al desarrollo de habilidades nuevas, que incluyen la creatividad, el pensamiento crítico, el razonamiento abstracto, entre otras que fueron promovidas gracias al programa diseñado.

Tabla 2 Resultados encontrados en la aplicación de las actividades. 

Por otra parte, se pudo observar que no todas las actividades son aptas para todos los estudiantes, pues algunos manifestaron sentirse más cómodos en algunas actividades y no en otras, sin embargo, los resultados aportaron positivamente a todo el grupo

Tabla 3 Percepción de los estudiantes con cada una de las actividades. 

Se observó que, aunque la mayoría de los estudiantes responden favorablemente a problemas abiertos, un 25% podría tener dificultades con este enfoque. Es posible que algunos estudiantes encuentren desafiante la falta de una solución única y la necesidad de emplear estrategias creativas. Por otra parte, los rompecabezas matemáticos muestran una buena aceptación, con un 80% de receptividad. Esta actividad parece ser bien recibida por la mayoría de los estudiantes, sugiriendo que el pensamiento lateral y las soluciones innovadoras son apreciados, al igual que las actividades de investigación, tuvieron una alta receptividad, esto sugiere que la mayoría de los estudiantes se sienten atraídos por la oportunidad de explorar y presentar soluciones matemáticas originales. Aunque la mayoría de los estudiantes responden positivamente, un 30% parece tener una receptividad menor hacia los juegos de estrategia matemática. Esto puede indicar que algunos estudiantes pueden encontrar desafíos en la aplicación de estrategias matemáticas en un contexto de juego. Los resultados también mostraron que el trabajo colaborativo es ampliamente cómodo para los estudiantes.

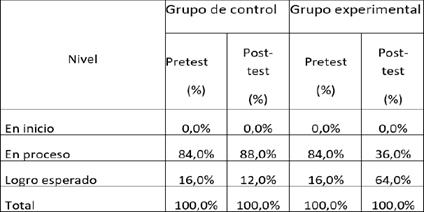
Al evaluar a ambos grupos en un post test, se observó que hubo importantes mejorías en la resolución de problemas del grupo experimental, sin embargo, en el grupo de control, se observó que las mejorías fueron escasas y que el conjunto de dudas era significativo. Además, se pudo verificar que no había una motivación ideal en el grupo de control, por el contrario, permanecía cierta desmotivación por la asistencia a las clases de matemáticas.

Tabla 4 Evaluación del pensamiento divergente del grupo de control y grupo experimental luego de la experiencia. 

Los resultados estadísticos proporcionan información valiosa sobre la eficacia de las estrategias utilizadas para impulsar el pensamiento divergente en los grupos control y experimental. En el pretest, el grupo experimental muestra un rendimiento ligeramente superior en términos de rango promedio y suma de rangos en comparación con el grupo control. Los resultados del postest sugieren que las estrategias implementadas en el grupo experimental tuvieron un impacto positivo en el pensamiento divergente, ya que experimentaron un aumento significativo en el rango promedio en comparación con el grupo control. La comparación directa de las sumas de rangos entre el grupo experimental y el grupo de control en ambos pretest y postest muestra que el grupo experimental supera consistentemente al grupo de control en ambas instancias. Este patrón indica que las estrategias aplicadas en el grupo experimental tuvieron un efecto positivo en el desarrollo del pensamiento divergente en comparación con el grupo de control. El aumento significativo en el rango promedio del grupo experimental desde el pretest hasta el postest (de 26.62 a 32.88) sugiere un impacto positivo y un desarrollo notable en el pensamiento divergente después de la implementación de las estrategias. Los resultados estadísticos respaldan la eficacia de las estrategias utilizadas en el grupo experimental para impulsar el pensamiento divergente, ya que mostraron un aumento sustancial en el rango promedio y la suma de rangos en comparación con el grupo control.

CONCLUSIONES

Los resultados sugieren que las estrategias implementadas en el grupo experimental fueron efectivas para impulsar el pensamiento divergente. El aumento significativo en el rango promedio en el postest indica un desarrollo positivo en las habilidades de pensamiento divergente de este grupo. Además, la comparación de las sumas de rangos entre el grupo experimental y el grupo control en ambos pretest y postest revela diferencias significativas. Estos hallazgos respaldan la idea de que las estrategias específicas aplicadas al grupo experimental tuvieron un impacto positivo en el pensamiento divergente en comparación con el grupo control.

Mientras que el grupo experimental percibió un aumento significativo en el rango promedio, el grupo control mostró una disminución en el postest. Esto podría indicar que las estrategias implementadas en el grupo experimental fueron particularmente efectivas al resistir cualquier disminución en el pensamiento divergente. De esta manera, la elección de un enfoque experimental parece haber influido en los resultados positivos observados en el grupo experimental. La implementación de estrategias específicas destinadas a fomentar el pensamiento divergente demostró ser más efectiva que la ausencia de tales intervenciones en el grupo control. Además, el aumento en el rango promedio del grupo experimental sugiere que los cambios inducidos por las estrategias aplicadas no fueron temporales, sino sostenibles. Esto podría indicar que las habilidades de pensamiento divergente desarrolladas podrían persistir más allá del período de intervención.

La observación de un desarrollo positivo en el pensamiento divergente en el grupo experimental respalda la idea de que estrategias específicas pueden ser relevantes y valiosas para el desarrollo cognitivo de los estudiantes. Esto destaca la importancia de implementar enfoques pedagógicos que vayan más allá de la enseñanza tradicional y fomenten habilidades de pensamiento crítico y creativo.