I. INTRODUCCIÓN
Las actuales demandas educativas destacan la necesidad de que los estudiantes desarrollen habilidades como la creatividad y la capacidad crítica para resolver problemas. Es esencial proporcionar técnicas y métodos, especialmente en el área de matemáticas, considerada una de las más desafiantes. A nivel de la Organización para la Cooperación y el Desarrollo Económicos (OCDE) uno de cada cuatro estudiantes de 15 años carece de competencias matemáticas 1. Por su parte, en Latinoamérica, los resultados de la prueba PISA 2018 revelaron bajos promedios, colocando a muchos países en el primer nivel. Solo estudiantes de Costa Rica, Chile, México y Uruguay superaron el 40% en el nivel mínimo. El Banco Interamericano de Desarrollo (BID) señala que la matemática es la peor materia para estudiantes de diez países latinoamericanos, situándolos en los últimos puestos a nivel mundial. Los desafíos en matemáticas persisten debido a la falta de empleo de estrategias por parte de los estudiantes. La resolución de problemas matemáticos requiere diversas habilidades y estrategias, por lo que es crucial que los estudiantes aprendan matemáticas a través de la solución de problemas y la construcción de nuevo conocimiento 2.
En los países latinoamericanos, la enseñanza de las matemáticas enfrenta una serie de desafíos significativos que obstaculizan el aprendizaje efectivo de esta disciplina. Uno de los problemas clave radica en la falta de recursos y capacitación adecuada para los educadores, lo que dificulta la implementación de metodologías pedagógicas innovadoras y la atención a las necesidades individuales de los estudiantes. Además, la brecha socioeconómica y la desigualdad en el acceso a una educación de calidad contribuyen a amplificar las disparidades en el rendimiento académico en matemáticas, dejando rezagados a muchos estudiantes y perpetuando ciclos de desventaja educativa. Por otra parte, según los resultados de la prueba PISA, Ecuador enfrenta desafíos significativos en el ámbito de las matemáticas. Los puntajes obtenidos en esta evaluación internacional reflejan un nivel de competencia matemática por debajo del promedio de la OCDE, lo que evidencia la necesidad de mejorar la calidad y el enfoque de la enseñanza de las matemáticas en el país 3. Esta situación subraya la urgencia de implementar políticas educativas efectivas que promuevan un aprendizaje más profundo y significativo en esta área, así como la capacitación continua de los docentes y la asignación de recursos adecuados para mejorar el rendimiento académico en matemáticas y, en última instancia, promover un desarrollo socioeconómico más equitativo y sostenible en Ecuador.
Las estrategias heurísticas están respaldadas por la UNESCO como enfoques pedagógicos eficaces para promover el pensamiento crítico, la resolución de problemas y el aprendizaje significativo en matemáticas y otras disciplinas. La UNESCO reconoce la importancia de estas estrategias para desarrollar habilidades cognitivas clave, así como para fomentar un enfoque más activo y participativo en el proceso de aprendizaje. Al promover el uso de estrategias heurísticas en los sistemas educativos de todo el mundo, la UNESCO busca mejorar la calidad de la educación y contribuir al desarrollo integral de los estudiantes, preparándolos para enfrentar los desafíos del siglo XXI y participar de manera efectiva en una sociedad cada vez más compleja y diversa 4.
En este sentido, este trabajo pretende formular un plan de estrategias heurísticas para su implementación en la enseñanza matemática en estudiantes de bachillerato, de manera que pueda considerarse su integración al programa educativo. De esta manera, se ha desarrollado un plan que abarca desde la identificación de las estrategias heurísticas más apropiadas para el nivel educativo y las necesidades específicas de los estudiantes, hasta la capacitación del personal docente en su aplicación efectiva en el aula 5. Además, se incluye la elaboración de materiales didácticos y recursos educativos que faciliten la incorporación de estas estrategias en el currículo escolar y promuevan un aprendizaje activo y significativo en matemáticas. Este plan se basa en investigaciones previas y buenas prácticas en el campo de la educación matemática, así como en las directrices y recomendaciones de organizaciones internacionales como la UNESCO y la OCDE, que respaldan el uso de estrategias heurísticas como un enfoque pedagógico efectivo para mejorar la calidad de la educación en matemáticas y promover el desarrollo integral de los estudiantes.
II. DESARROLLO
Las estrategias heurísticas desempeñan un papel crucial en el ámbito de las matemáticas debido a su capacidad para estimular el pensamiento creativo y la resolución de problemas. En tal sentido, los aportes analizados, son los siguientes:
A. Capacidades de resolución de problemas matemáticos
Conceptualizada como habilidades adquiridas para identificar y resolver problemas, aplicar conocimientos en diferentes contextos y desarrollar el pensamiento matemático en la vida cotidiana. El objetivo es desarrollar diferentes maneras de pensar y actuar con la matemática en situaciones donde sea posible intervenir conscientemente en la realidad. Resolver un problema implica interpretar una situación matemática, y al desarrollar y revisar esta situación, se comprenden e incorporan conocimientos fundamentales de matemáticas 6.
La resolución de problemas es crucial para el desarrollo de competencias en los estudiantes, considerándola esencial para promover habilidades y capacidades. Se ha convertido en una táctica de fácil aplicación en la enseñanza diaria, brindando a los alumnos la disposición para abordar circunstancias y desafíos que requieren su resolución. Asimismo, implica el análisis de situaciones, la identificación de patrones y la selección de estrategias para llegar a soluciones efectivas. Este proceso contribuye al desarrollo del pensamiento crítico, esencial en la toma de decisiones informadas 7.
Cabe resaltar que, el desarrollo de las capacidades matemáticas no solo es esencial para el éxito académico, sino que también tiene un impacto significativo en la vida cotidiana y se fomenta el desarrollo cognitivo y emocional de los individuos. Esta visión se centra en la importancia de presentar problemas matemáticos que se ajusten al nivel de conocimiento de los estudiantes para despertar su interés. Sin embargo, en la práctica muchos docentes proporcionan problemas rutinarios y poco desafiantes, lo que hace que las matemáticas resulten aburridas y carentes de significado para los alumnos. La solución propuesta es superar este problema mediante la creación de preguntas y problemas que generen curiosidad y representen un desafío, transformando así la manera de enseñar matemáticas. Dado que se reconoce la dificultad que muchos estudiantes enfrentan en esta habilidad, se busca contribuir a su desarrollo para mejorar su competitividad. En última instancia, se destaca la importancia de crear un entorno de aprendizaje donde los alumnos disfruten del proceso de aprender matemáticas.
Al resolver problemas matemáticos, los estudiantes, deben no solo abordar cuestiones de cantidades, sino también determinar si la solución requiere una aproximación o un cálculo exacto. Esto implica la selección de estrategias, métodos, unidades de medida y recursos adecuados basándose en las características específicas del problema. Durante este proceso, se emplea el razonamiento lógico para comparar datos, explicar situaciones mediante analogías e inferir características a partir de instancias específicas. La capacidad de resolver problemas matemáticos, también, abarca la resolución de problemas relacionados con patrones, comparaciones y transformaciones, centrándose en identificar, comprender y describir reglas o pautas en secuencias o conjuntos de datos. También destaca la importancia de abordar problemas geométricos, de desplazamiento y ubicación en el espacio, implicando la comprensión y descripción de figuras y objetos, así como el análisis de sus movimientos y cambios de posición 8.
Desde la perspectiva de resolver problemas matemáticos, se incluyen situaciones que requieren la manipulación de datos, el análisis de información y la toma de decisiones en contextos de incertidumbre. Esto implica recopilar, organizar y procesar datos de manera significativa utilizando herramientas como hojas de cálculo y gráficos. La gestión de datos abarca la evaluación de información considerando la variabilidad o falta de precisión, utilizando métodos estadísticos y probabilísticos. Tomar decisiones bajo incertidumbre implica considerar diversas posibilidades y escenarios, utilizando técnicas como el análisis de riesgos y la valoración de opciones para seleccionar la mejor alternativa en situaciones donde la información puede ser limitada o imprecisa 8.
La resolución de problemas matemáticos se fundamenta en teorías psicológicas, principalmente la teoría cognitiva, que examina procesos mentales como percepción, atención, memoria y pensamiento. Jean Piaget, en su teoría del desarrollo cognitivo, establece etapas secuenciales y universales, influyendo en la comprensión matemática en diversas fases. Los estudiantes en estudio se encuentran en la etapa de operaciones formales, exhibiendo pensamiento abstracto y habilidades cognitivas avanzadas. La teoría cognitiva en la resolución de problemas matemáticos se enfoca en representación mental, estrategias de resolución, metacognición y aprendizaje activo. Examina cómo las personas representan mentalmente los problemas y emplean estrategias, incorporando la reflexión sobre procesos cognitivos y el aprendizaje activo. Además, la teoría sociocultural de Vygotsky destaca la influencia del entorno social en el aprendizaje. Desde la perspectiva constructivista, resolver problemas es fundamental para la construcción del conocimiento, especialmente en matemáticas. El enfoque constructivista subraya la colaboración, el intercambio de ideas y la toma de decisiones para encontrar soluciones. La aplicación de estrategias heurísticas, respaldada por la teoría constructivista, guía la búsqueda de soluciones y enriquece el aprendizaje significativo 9,10.
B.Está Estrategias heurísticas
Las estrategias heurísticas son enfoques para resolver problemas matemáticos, los cuales deben ser desafiantes, que involucren la formulación de preguntas efectivas, la conexión con conocimientos previos y el aprovechamiento de errores. Es importante que estas estrategias aborden la resolución de problemas difíciles y fomentan su aplicación en la vida diaria 11. Por otra parte, Las estrategias heurísticas son muy relevantes en un mundo cambiante y deben utilizarse para resolver problemas de diferentes niveles de complejidad. En el aula, se busca fomentar la autonomía y habilidades como el pensamiento crítico, la comunicación y la colaboración 12. Específicamente se pueden implementar estrategias heurísticas como actuar, cambiar el punto de vista, diagramar, hacer adivinanzas y verificaciones, razonamiento lógico, indagar sobre un patrón, realizar una lista sistemática, hacer una tabla, hacer suposiciones, replantear problemas, reducir la complejidad, abordar una porción del problema, considerar un problema relacionado, emplear un modelo, utilizar una ecuación, aplicar el concepto de antecedente y consecuente y trabajar en reversa 13.
Las dimensiones de las estrategias heurísticas incluyen tres variables aplicadas al proceso de resolución de problemas. En la primera se destacan las técnicas de visualización, que involucran el uso de recursos visuales, como gráficos y figuras, para comprender y resolver problemas. Se mencionan estrategias como la creación de diagramas y la elaboración de tablas. En la segunda se abordan las técnicas de exploración, donde el estudiante examina y registra las dificultades a resolver. Estrategias como el ensayo y error, la búsqueda de patrones y la realización de suposiciones se destacan como métodos para enfrentar y aprender de los problemas. La tercera dimensión se centra en las técnicas de reformulación, que implican abordar un problema desde una perspectiva diferente. Se mencionan estrategias como la búsqueda de analogías, donde se encuentran similitudes con problemas ya resueltos, y el enfoque de "comenzar por el final", retrocediendo desde el resultado deseado para identificar los pasos necesarios para llegar a la solución 14.
Otras Investigaciones han corroborado que la aplicación de estrategias heurísticas tiene muchos beneficios 9,11. Promueven el pensamiento creativo al desafiar a los estudiantes a abordar problemas matemáticos de manera imaginativa, estimulando la exploración y experimentación para identificar patrones. Además, Desarrollan habilidades efectivas de resolución de problemas al enseñar a descomponer situaciones complejas en soluciones manejables. También Destacan por su flexibilidad, aplicándose a diversos problemas y preparando a los estudiantes para desafíos cambiantes. En este sentido, Las habilidades adquiridas trascienden el aula, siendo útiles en situaciones de la vida real donde la resolución de problemas matemáticos es esencial. Al fomentar que los estudiantes descubran soluciones por sí mismos, estas estrategias aumentan la motivación y la confianza, manteniendo un interés continuo y contribuyendo a un aprendizaje matemático más significativo 6,14,15.
Las estrategias heurísticas se fundamentan en la teoría del desarrollo cognitivo de Piaget y García 15,10 quienes proponen que el aprendizaje se logra a través de dos procedimientos complejos: la asimilación y la acomodación. Estos procesos fomentan la adaptación y actúan como motores del crecimiento intelectual, llevando al individuo a incorporar constantemente nuevos conocimientos en sus estructuras mentales y avanzar hacia niveles superiores 16.
También Ausubel 8 y su teoría del aprendizaje significativo, es un aporte para las estrategias heurísticas porque indica que este tipo de aprendizaje se logra al conectar la información reciente con los conocimientos previos del estudiante. Además, destaca la importancia de considerar la variedad de conceptos y propone que tanto la recepción de información como el descubrimiento contribuyen al aprendizaje significativo 16. Asimismo, Bruner 12 con su teoría del aprendizaje por descubrimiento, aboga para que los estudiantes sean participantes activos que construyan sus propios conocimientos. En este contexto, el autor propone que los alumnos, motivados por la curiosidad, aprendan a explorar y descubrir con la guía del docente, quien proporciona recursos para manipular objetos directamente. Además, destaca la importancia de actividades como la observación, comparación, análisis y reflexión, necesarias para la aplicación de las estrategias heurísticas, y enfatiza que la verdadera comprensión del conocimiento se manifiesta al aplicarlo en diversos contextos 9.
III. METODOLOGÍA
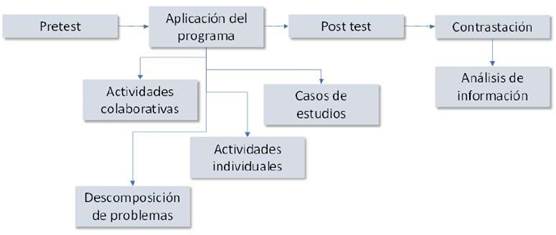
Para llevar a cabo este estudio, se adoptó un enfoque mixto de tipo aplicado, con un diseño experimental. En la figura 1 se describe el proceso de investigación realizado, donde se observa que la muestra fue sometida a un pretest para conocer sus características iniciales en resolución de problemas, luego se implementó el programa de estrategias heurísticas diseñado y se midió nuevamente la experiencia, confirmando una importante diferencia antes y después de las actividades.
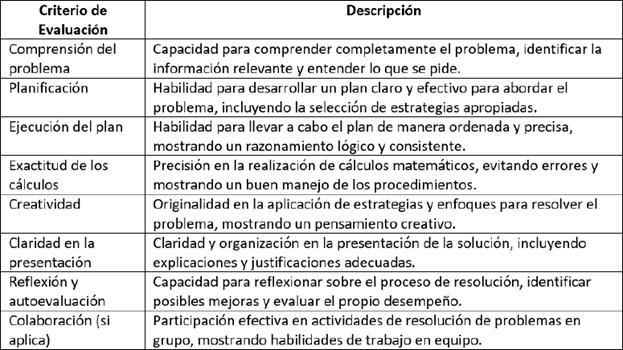
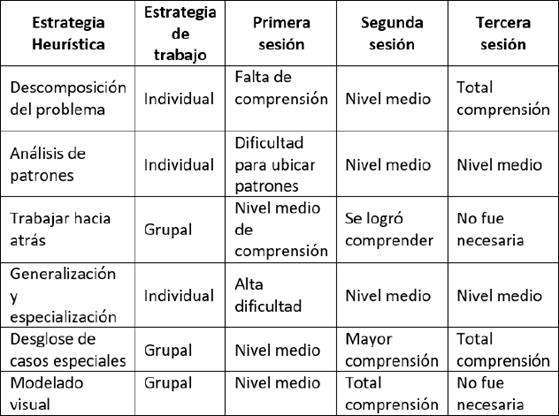
Para la prueba inicial, se evaluaron los aspectos descritos en la tabla 1, que permitían conocer la forma en que los estudiantes realizaban los problemas matemáticos, y de esta manera poder conocer las principales debilidades que presenta el grupo de estudiantes y con ello generar el plan de acción.
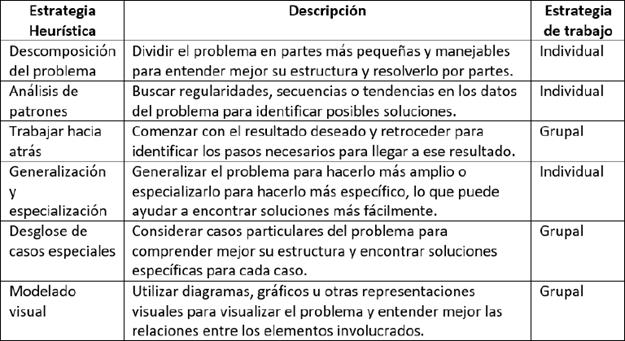
Una vez conocidas las características de los estudiantes en la resolución de problemas, se diseñaron las estrategias heurísticas de la tabla 2, donde se hizo énfasis en la comprensión y análisis.
.El plan diseñado se implementó durante cuatro semanas, con tres sesiones cada una. Además, incluyó la retroalimentación necesaria para ir haciendo los ajustes de mejora del plan y poder replicarlo en situaciones futuras.
IV. RESULTADOS
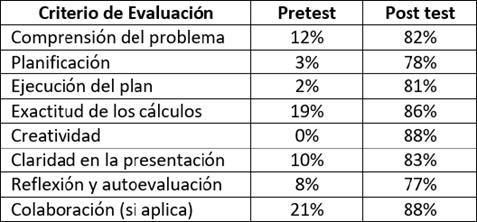
Los resultados encontrados en el pretest y post test se describen en la tabla 3, donde se observa que, al inicio, solo un pequeño grupo de estudiantes lograba formular la solución de problemas coherentes antes de aplicar el plan de estrategias heurísticas. Se observó que el trabajo grupal ofrecía buenas expectativas, pero debía también atenderse la comprensión individual, dado que los trabajos grupales muchas veces no alcanzan un apropiado aprendizaje significativo, en el caso específico de problemas matemáticos. De manera que se alternaron las actividades del plan para que hubiese algunas colaborativas y otras individuales. Por otra parte, se observó una importante mejora el post test, reflejando que las actividades heurísticas aportaron en la comprensión y solución de los problemas.
Por otra parte, los resultados encontrados al aplicar el plan de estrategias heurísticas, se describe en la tabla 4, donde es posible observar que hubo una buena acogida en el cambio de metodologías para resolución de problemas.
Tabla 4 Ficha de evaluación utilizada en el pretest para evaluar aspectos de Coordinación y motricidad.
Por su parte, los resultados del post test revelaron que más del 85% de los estudiantes alcanzó un nivel alto de comprensión de los problemas y logró resolverlos de manera efectiva. Además, se aprecia que cada estrategia requirió más de una sesión, lo que demuestra que el plan debe ser implementado de forma permanente.
A. Tratamiento estadístico
Se observó que en el Pretest la media alcanza un valor de 9,25% y la desviación estándar un valor de 7,97%, mientras que en el Post test, se obtuvo una media de 80,14% y una desviación estándar de 31,85%. El análisis de los valores de la media y la desviación estándar proporciona una visión más profunda sobre la distribución y la consistencia de los datos. En el pretest, se observa una media relativamente baja, lo que sugiere un rendimiento generalmente bajo en los criterios de evaluación antes de la intervención. Además, la desviación estándar indica una variabilidad considerable entre los puntajes de los participantes, lo que sugiere que algunos estudiantes podrían haber tenido un desempeño mucho peor que otros en ciertos criterios.
Por otro lado, en el post test, la media se incrementa significativamente, indicando una mejora sustancial en el desempeño general de los estudiantes después de la intervención. Sin embargo, la desviación estándar aumenta, lo que sugiere una mayor variabilidad en los puntajes entre los participantes después de la intervención. Esto podría indicar que, si bien la mayoría de los estudiantes han mejorado, algunos todavía muestran niveles más bajos de desempeño en ciertos criterios de evaluación.
Los valores de la media y la desviación estándar proporcionan una indicación clara de la efectividad general de la intervención en mejorar el rendimiento de los estudiantes en la resolución de problemas matemáticos, pero también señalan la necesidad de abordar la variabilidad individual en el desempeño para asegurar que todos los estudiantes alcancen su máximo potencial.
El coeficiente de correlación de Pearson (r) entre los puntajes del pretest y del post test proporciona información sobre la relación lineal entre estas dos variables. Un valor de r cercano a 1 indicaría una correlación positiva perfecta, lo que significa que a medida que los puntajes del pretest aumentan, también lo hacen los puntajes del post test. Por otro lado, un valor de r cercano a -1 indicaría una correlación negativa perfecta, lo que significa que a medida que los puntajes del pretest aumentan, los puntajes del post test disminuyen. Un valor de r cercano a 0 indicaría una correlación débil o inexistente entre las dos variables.
Después de realizar los cálculos, el valor específico de r se determinó, lo que permitió realizar un análisis más detallado de la relación entre los puntajes del pretest y del post test. En este sentido, el valor de Pearson fue de 0,86, cercano a 1, lo que indica una correlación positiva fuerte entre los puntajes del pretest y del post test. Esto indica que los estudiantes que obtuvieron puntajes más altos en el pretest también obtuvieron puntajes más altos en el post test, lo que respalda la efectividad de la intervención en mejorar el rendimiento en la resolución de problemas matemáticos. Esto permitió deducir que otro factor que favorece la comprensión de problemas matemáticos es la educación previa que han tenido los estudiantes, lo que contribuye a una mejor comprensión de las estrategias. Esto sugiere que un plan de estrategias heurísticas para la resolución de problema debe ser aplicado de forma permanente en la enseñanza, y que deben hacerse los ajustes necesarios para ir incorporando nuevas estrategias según el nivel de estudio, así como fortalecer las sesiones de trabajo.
CONCLUSIONES
Las estrategias heurísticas no solo mejoran las habilidades específicas de resolución de problemas, sino que también contribuyen al desarrollo integral de los estudiantes, fortaleciendo aspectos cognitivos, emocionales y metacognitivos de su aprendizaje matemático. En este sentido, las estrategias heurísticas dotan a los estudiantes de herramientas y enfoques sistemáticos, capacitándolos para abordar problemas matemáticos con mayor eficacia, facilitando la identificación y aplicación de métodos adecuados para distintos tipos de problemas, potenciando la habilidad de los estudiantes para seleccionar y emplear estrategias pertinentes.
La utilización de estrategias heurísticas promueve el pensamiento crítico al involucrar a los estudiantes en la toma de decisiones, el análisis de situaciones y la evaluación de posibles soluciones, cultivando habilidades que les permiten reflexionar sobre su propio proceso de resolución de problemas, identificando tanto sus fortalezas como áreas de mejora. De esta manera, las habilidades adquiridas mediante estrategias heurísticas son transferibles a diversos contextos y tipos de problemas matemáticos y los estudiantes pueden aplicar su comprensión a situaciones del mundo real, estableciendo conexiones entre la teoría matemática y sus aplicaciones prácticas.
La resolución de problemas mediante estrategias heurísticas implica la participación activa de los estudiantes en el proceso de aprendizaje y se fomenta en ellos la exploración, el descubrimiento y la experimentación, contribuyendo a un aprendizaje más profundo y duradero.












 uBio
uBio