Concepciones en la enseñanza del cálculo*

Clemente Moreno

Colegio Universitario de Caracas

Pablo Ríos

UPEL, Instituto Pedagógico de Caracas, IPC

Resumen

El presente estudio tiene como objetivo establecer los procedimientos didácticos aplicados, tanto en la concepción clásica como en la moderna, para la enseñanza del cálculo a nivel universitario con el propósito de promover un escenario educativo que integre la enseñanza algorítmica propia de la concepción clásica con la enseñanza heurística proveniente de la praxis docente basada en la solución de problemas. Se propone, así, el uso de una concepción moderna con la incorporación de estrategias metacognitivas que regulen la complementariedad de estas concepciones. Esta investigación de carácter documental encuentra su sustento teórico en los principios filosóficos asociados con el pensamiento constructivista de la educación. Por otra parte, se sugiere la promoción de escenarios educativos para la enseñanza de la matemática que integren, de modo estratégico, las diferentes concepciones pedagógicas para adecuar la enseñanza del cálculo a las exigencias que la sociedad actual demanda de la escuela, pues tal integración redunda en la formación de aprendices autónomos aptos para manejar los esquemas de razonamiento matemático en la interpretación de un mundo donde la matemática es esencial para el ser social.

Palabras clave: Enseñanza del cálculo: enseñanza heurística y algorítmica, metacognición.

ABSTRACT

Teaching Calculus Conceptinos

The objective of this article is to describe applied didactical procedures, in the classical and modern conceptions, to teach calculus at the higher education level, with the purpose to promote educational scenarios that integrate algorithmic teaching, characteristic of classical conception, with heuristic teaching, characteristic of the problem solving educational praxis. The article proposes the use of a modern conception that incorporates metacognitive strategies. This documental research has its theoretical basis on constructivism. on the other side, it proposes the promotion of educational scenarios to teach mathematics integrating, strategically, different pedagogical conceptions to teach Calculus considering the demands society sets on the school. This integration will contribute to educate autonomous learners capable to think mathematically to interpret the world, a world where mathematics is essential for the social being.

Key words: Calculus Teaching, Heuristic and Algorithmic Teaching, Metacognitive Strategies.

* Recibido: septiembre 2005.

Aceptado: mayo 2006.

Introducción

Concebir el aprendizaje de la matemática como el proceso donde el docente junto a los estudiantes reelaboran las ideas, principios y conocimientos que éstos necesitan para desenvolverse en un mundo fuertemente matematizado, es concebir la enseñanza aprendizaje de esta disciplina como un acto educativo flexible que exige de los alumnos intuición y creatividad para que alcancen autonomía en sus aprendizajes y, de los docentes, el desarrollo de una práctica educativa que garantice el éxito de esta exigencia.

Algunos de los orígenes de este escenario pueden encontrarse, entre muchos otros, en los trabajos adelantados por la Comisión Internacional de Enseñanza de la Matemática surgida en el IV Congreso Internacional de Matemática celebrado en Roma en 1908. En ese caso, la comisión que bajo la dirección de Félix Klein, auspició la formación de profesores en el área de matemática para educación media y seleccionó, de manera estructurada, los contenidos programáticos que debían enseñarse en este nivel educativo. Esta acción investigativa se frena con los avatares de las guerras mundiales produciéndose un letargo que vuelve a despertar en el congreso de matemática de Royaumont en 1959. Allí, Jean Dieudonné propuso modificar los programas de matemática que se enseñaban en bachillerato y excluyó de éstos los contenidos derivados de la geometría euclídea para sustituirlos por el estudio de la teoría de conjuntos, de la lógica, el álgebra lineal elemental y algo de cálculo. Estos contenidos debían ser enseñados desde una perspectiva axiomática para conducir el trabajo docente a fomentar el rigor matemático en el aprendiz.

Esta manera de presentar la disciplina fue criticada en la voz de René Thom en el Congreso de Exeter de 1972, quien argumentó que la propuesta curricular de Dieudonné sin la geometría euclídea, despojaba a la enseñanza básica de una cantera inagotable de contenidos y problemas de relevancia en la formación de los jóvenes, para sustituirlo por un material estructurado de manera axiomática que a su juicio frenaba la conjetura, no promovía la manipulación operativa del espacio, limitaba la adquisición de las ideas matemáticas e impedía la formación de las estructuras del pensamiento que se pretendían desarrollar con la aplicación de ese currículo. Guzmán (1993), en relación con esta polémica indica que los problemas ocasionados con la incorporación de la llamada matemática moderna fueron más que las posibles ventajas que se había pensado conseguir, tal como el rigor en la fundamentación, el entendimiento de las estructuras matemáticas, la modernidad y la proximidad a lo que hacían los matemáticos profesionales. Sin embargo, conviene destacar la influencia que sobre la enseñanza de la matemática ejerció la controversia de los principios filosóficos y epistemológicos discutidos en estos movimientos de reformas curriculares.

Así, en las tres últimas décadas del siglo XX, la referida polémica, promovió en el panorama educativo internacional, un movimiento de alerta permanente sobre el avance y desarrollo del quehacer educativo en matemática a todos los niveles, además de motorizar, según García (1999), la idea de que una de las actividades básicas de la matemática es la de organizar y estructurar la información que subyace en un problema, identificando las relaciones y regularidades de las estructuras matemáticas inmersas en la situación problemática. Matematización que a su parecer la escuela ha realizado siguiendo estilos de enseñanza donde destacan el estructuralismo, el mecanicismo, el empirismo y el realismo.

Por una parte, los estructuralistas conciben la matemática como una disciplina lógico-deductiva y encaminan su enseñanza a deducir las verdades dadas en teoremas a partir de una axiomática preestablecida; los mecanicistas piensan que la matemática consiste en desarrollar procedimientos que le permitan conocer los conceptos básicos de la disciplina y en consecuencia, la docencia debe dirigirse a la enseñanza de reglas que conduzcan al estudiante a la manipulación de fórmulas y símbolos; los empiristas consideran que los conocimientos matemáticos provienen de la experiencia y dirigen su práctica docente a explorar y desarrollar nociones matemáticas sin preocuparse por la formalidad de la disciplina; quienes se ubican en el realismo comparten con los empiristas la génesis del saber matemático, pero su enseñanza se fundamenta en la invención o reconstrucción de la matemática escolar en analogía con el proceder del matemático en la creación de su ciencia.

Por su parte Carrillo (2000), opina que la actividad matemática en la escuela se realiza atendiendo a los principios derivados de las concepciones platónica, instrumentalista y de solución de problemas; perspectivas que a su parecer generan los estilos tradicional, tecnológico, espontáneo e investigativo en la enseñanza de la disciplina. Los platónicos ven la matemática como una ciencia abstracta organizada en una estructura lógica que le da un carácter objetivo, absoluto y libre de valores, tal caracterización fundamenta el estilo tradicional de enseñanza de la matemática basado en el esquema transmisión-recepción; los instrumentalistas conciben la matemática como un conjunto organizado de conocimientos preexistentes de carácter utilitario de los cuales se enseñan reglas y herramientas que sirven de base para el aprendizaje de otras ciencias, siguiendo una práctica de enseñanza que simula procesos de construcción apoyados en recursos tecnológicos; quienes derivan el conocimiento matemático de la solución de problemas ven la disciplina como un edificio en remodelación permanente que se amolda al contexto social, cultural y científico donde se realiza la edificación. En esta perspectiva se enmarcan los estilos espontáneo e investigativo que conciben la enseñanza como una acción dirigida a promover un aprendizaje que integra conceptos, procesos y estrategias en la reconstrucción autónoma de un conocimiento matemático útil.

Desde nuestra perspectiva, estos estilos de enseñanza se enmarcan en dos concepciones que se afianzan en estrategias didácticas distintas para potenciar el desarrollo de las estructuras del pensamiento del estudiante y dotarlo de las herramientas de análisis inherentes al proceso de matematización escolar. La primera que puede denominarse concepción clásica, ve la matemática como un saber estructurado con escasa variabilidad y concibe al docente como un instructor que dirige su actividad a la exposición de conceptos ilustrados con ejemplos, seguidos de ejercicios sencillos cuya dificultad va incrementando en la medida que desarrolla la clase. La segunda, que puede tildarse de concepción moderna, ve la matemática como un saber hacer que incluye conjeturas, pruebas y refutaciones de las ideas matemáticas incluidas en la problemática que se analiza, de modo que la enseñanza que surge de allí, ve al maestro como un formador que invita a descubrir, inventar y probar ideas a través de la argumentación y de la reflexión crítica.

La enseñanza de las ideas del cálculo a nivel universitario, no es ajena a estas concepciones. De un lado se ubican aquellos docentes que bajo la concepción clásica, limitan su acción educativa a repetir los conceptos matemáticos tal como aparecen en los libros de texto o en la misma forma en que le fueron enseñados, reduciendo sus clases a una algoritmización de los conceptos del cálculo que los estudiantes contemplan, memorizan y repiten en los exámenes, lo que de acuerdo con Artigue, Douady, Moreno y Gómez (1995), es una enseñanza marcada por la manipulación de fórmulas evidenciada en la determinación del límite, derivada o integral de una función, en lugar del análisis de estos conceptos y su aplicación en la solución de los problemas del entorno académico y social del estudiante. Estas observaciones muestran la inclinación de los autores por las estrategias didácticas que orienten el proceso creador inmerso en la matemática escolar y que a juicio de éstos se logra con una enseñanza fundamentada en la solución de problemas, praxis que se corresponde con la concepción moderna de la enseñanza, la cual según Guzmán (1993), es el método más invocado para llevar a cabo el principio general del aprendizaje activo, toda vez que enfatiza en la utilidad de la apropiación de los contenidos matemáticos tanto en el desarrollo de los procesos del pensamiento como en los procesos de aprendizaje.

De un lado, estas concepciones dejan ver que el proceso enseñanza aprendizaje de la matemática es un problema complejo cuyas variables requieren un estudio que supera los propios conocimientos matemáticos hasta alcanzar otras disciplinas, más aún a nivel universitario donde se cree que basta con saber matemática para enseñarla, por ello es común encontrar un gran porcentaje de profesores de esta disciplina con sólidos conocimientos matemáticos, lo cual es una condición necesaria, pero no suficiente para adelantar el proceso de enseñanza aprendizaje de la matemática. La carencia de formación pedagógica y el desconocimiento de los métodos de investigación en ciencias sociales conforman una limitante que impide enfrentar de manera exitosa los problemas que emergen de los procesos de aprendizaje que plantea la enseñanza de la matemática.

Del otro lado, imponer una tendencia dirigida a convencer a los profesores casi sin evidencia empírica, de conducir su praxis docente apegados a una concepción de enseñanza que dice afianzar su quehacer docente en procedimientos heurísticos, en detrimento de la concepción que sustenta su práctica educativa en procedimientos algorítmicos, es desde nuestra percepción una dirección que puede conducirnos a situaciones similares a las vividas en los años 60 y 70 del siglo pasado con la implementación de la llamada matemática moderna. Enderezar el rumbo es estar a tono con una perspectiva epistemológica reciente, que al decir de Velasco, 2000, ha asumido que los medios heurísticos deben concebirse como subordinados a la estructura algorítmica de la ciencia, razón por la cual estos procedimientos no deben considerarse de manera aislada, sino como los elementos de un continuo que el maestro puede utilizar solos o acompañados dependiendo tanto del momento y el contexto como de los aportes que al respecto realizan las teorías del aprendizaje.

Asumiendo por una parte, que la enseñanza de la matemática debe ser una tarea encaminada a suministrar información clara del tópico en estudio a través de ejemplos y descripciones que promuevan en el estudiante una práctica reflexiva que dé lugar a la experimentación, a las aproximaciones sucesivas, a las tentativas exitosas y estériles de las actividades que conducen al aprendizaje. Por otra, la necesidad de que el sujeto enfrente lo aprendido ante las demandas exigidas por la escuela bajo la orientación clara y precisa del docente, de modo que el aprendizaje de esta disciplina sea una actividad similar a la que sigue el matemático en la creación de su ciencia, por lo que las acciones deben encaminarse a organizar y estructurar la información relevante del problema en estudio para descubrir las relaciones y regularidades que lo caracterizan.

Este artículo se propone recabar información acerca de los procedimientos didácticos más frecuentes, inmersos en ese par de concepciones de la enseñanza del cálculo, a fin de promover una integración entre estas estrategias, fundamentada en los aportes de las teorías de la educación. Estos elementos de convergencia deberán redundar en la creación de escenarios de aprendizaje donde el maestro retire las ayudas que suministra a los estudiantes en la misma medida que éstos alcanzan autonomía en la solución de los problemas que se le plantean en la enseñanza de la matemática.

Se busca, además, destacar el papel instrumental de la matemática que se refleja tanto en la formación del pensamiento lógico formal como en el desarrollo de habilidades y destrezas en el manejo de procesos algorítmicos. Las reflexiones adelantadas en esta investigación, encuentran su justificación en la potencialidad de las nociones de cambio manejadas en las ideas del cálculo que se discuten en las aulas universitarias, ellas forman parte tanto del lenguaje como de los procedimientos seguidos en la mayoría de las ciencias, lo que hace de esta rama de la matemática la herramienta clave en el manejo del nivel de preparación científica y tecnológica de las nuevas generaciones.

Concepción clásica y moderna en la enseñanza de la matemática

Parece acertado iniciar la discusión en torno a ese par de concepciones en la enseñanza del cálculo, destacando la necesidad de poner de lado la creencia generalizada de que la enseñanza de la matemática es una tarea fácil, que puede llevar a cabo cualquier persona con carácter y sentido común que conozca los principios básicos de la disciplina, lo cual excluye por supuesto a los buenos profesores de todos los tiempos que aún con escasos conocimientos de los aportes procedentes de la epistemología y la psicología que enriquecen de manera significativa la práctica educativa, hacen de la actividad académica un espacio donde la enseñanza simula las maneras de producir conocimientos matemáticos. En esta discusión nos anima la idea de incitar un análisis reflexivo acerca del quehacer diario en esa compleja, pero excitante tarea de promover el aprendizaje autónomo de la matemática.

En esta tarea es oportuno hacer una distinción entre quienes conciben la matemática como una ciencia intensamente dinámica y cambiante proveniente del saber hacer, y los que la perciben como una ciencia que reúne un conjunto de saberes acabados y rígidos, que de acuerdo con Guzmán (1993), promueven diferencias en las praxis docentes que generan aprendizajes diferentes. La primera, incita el desarrollo de los procesos mentales propios de la matemática y la segunda, a la recepción de contenidos que esperan la ocasión de ser aplicados y que en opinión del autor precitado se tornan obsoletos en períodos de tiempo marcados por el avance tecnológico, así por ejemplo el cálculo de la derivada de una función que es una actividad a la que suele dedicársele mucho tiempo, carece de relevancia en la actualidad, pues con la calculadora o la computación puede determinarse en fracciones de segundo, para este autor lo que es más o menos permanente en el individuo, son los procesos cognitivos que le permiten abordar con éxito los problemas presentes en el entorno, sin embargo no niega el papel de los procesos algorítmicos y de la automatización en la organización y consolidación de lo aprendido, razón que justifica el análisis de las características que definen a las concepciones de la enseñanza a las que nos estamos refiriendo.

Concepción clásica en la enseñanza del cálculo

De acuerdo con Vera y Silva (s/f), la visión tradicional de la praxis docente en matemática donde se enmarca la concepción clásica de la enseñanza del cálculo, se limita al desarrollo de unas clases que se reducen a exposiciones de conceptos planteados en situaciones problemáticas que se ilustran con ejercicios o problemas descontextualizados, donde el énfasis se coloca en la memorización de técnicas y reglas que no tienen vinculación con la realidad y dan la impresión de que la matemática sólo existe en el momento de la clase. Desde esta óptica, la enseñanza por ejemplo de la noción de la primera derivada de una función en un punto como la pendiente de la recta tangente a la curva en ese punto⁽¹⁾, partiría del estudio de la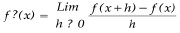

expresión como una situación problemática, que a partir de su evaluación en un punto x_o del dominio de f' permite determinar la pendiente de la recta, continua con el ejercicio de calcular la primera derivada de algunas funciones y su evaluación en ciertos puntos del dominio de estas funciones y culmina con problemas donde se invita al estudiante a calcular la pendiente de la recta tangente a una curva en un punto dado. Esta praxis al decir de García (1999), sigue un estilo expositivo en la transmisión de un conocimiento acabado y abstracto que genera una enseñanza plagada de definiciones y de procedimientos algorítmicos, promueve un conocimiento caracterizado por la certidumbre y la carencia de dudas que limitan la consideración de respuestas alternas.

De este modo, los problemas inmersos en los conceptos del cálculo, que en el caso citado, para una clase de matemática en un contexto económico, pudiera referirse al estudio de los fenómenos marginales (representados en la idea de tangencia) que ocurren al margen de un proceso de producción (representado en la curva de la función) y que encierra un conjunto de situaciones sin soluciones evidentes, son transformados en ejercicios que el profesor resuelve de manera certera y en forma lineal, sin dar espacio a la discusión, a la conjetura, a la experimentación. Este estilo de enseñanza que conduce a la desproblematización de los problemas, al decir de Gil (1993), coloca de manifiesto las deficiencias de la enseñanza por transmisión, puestas en evidencia en el hecho de que a lo sumo promueven la solución de ejercicios similares a los tratados en clase, pero que a su juicio no enseña como abordar un verdadero problema, por lo que cualquier cambio respecto a los ejercicios hechos en clase generan dificultades insuperables en los estudiantes que optan por abandonar la búsqueda de la solución.

En opinión de Beltrán (1993), esta concepción de la enseñanza tiene sus raíces en la teoría conductista que concibe el aprendizaje como el registro de una serie de impresiones sensoriales provenientes de los elementos componentes del fenómeno en estudio, donde el papel decisivo en el proceso de aprendizaje lo desempeñan las actividades planeadas y ejecutadas por el maestro en la transmisión de unos conocimientos que el alumno guarda en su memoria para dar respuesta a las tareas que le plantea la escuela.

Una visión renovada de la fundamentación teórica de esta concepción se encuentra en las ideas de Ausubel, Novak y Hanesian (1986) quienes han resaltado el papel guía del profesor en el control de la dispersión que puede generar el aprendizaje por descubrimiento y el papel de las estructuras conceptuales de los estudiantes en la adquisición de los nuevos conocimientos, dejando en claro la existencia de un modelo coherente de enseñanza aprendizaje por transmisión recepción que puede generar un aprendizaje significativo en la medida que la asimilación sea el producto de un proceso activo que promueva la diferenciación y reconciliación integradora entre lo que sabe el estudiante y la nueva información o la de un aprendizaje memorístico si la praxis docente apunta en dirección contraria, vale decir, si la enseñanza se limita a describir, ilustrar y manipular los conceptos que se están enseñando, sólo a través de procesos algorítmicos que nieguen la posibilidad de emitir juicios y experimentar e incluso de analizar los resultados.

Sin embargo, aún cuando el énfasis de la instrucción se coloca en la información presentada en temas, tal como la noción de cambio, expresado en estructuras algebraicas que establecen una relación de dependencia entre variables, donde se destacan los elementos que conforman el modelo de relación funcional, el aprendizaje puede tornarse significativo en el sentido de Ausubel en la medida que el estudiante se torne cognitivo comprometiéndose con los procesos de entendimiento de esas partes de la estructura algebraica que le permiten avanzar paso a paso hacia la comprensión del fenómeno variacional. Esta concepción del aprendizaje puede considerarse como el punto frontera entre el aprendizaje que se promueve en la concepción clásica y que Beltrán (1993), denomina aprendizaje por adquisición de respuestas y el aprendizaje que se genera en la concepción moderna.

Concepción moderna en la enseñanza del cálculo

Esta concepción habla de un aprendizaje como construcción de significados para que el estudiante construya el conocimiento basándose en su bagaje cultural y en las orientaciones provenientes del profesor que ya no es visto como un transmisor de saberes, sino como el otro participante del proceso de aprendizaje que junto al alumno construye el conocimiento, lo cual significa que su actividad se dirige a promover la organización, interpretación y comprensión del material informativo para que sea el mismo estudiante el que decida el qué y el cómo de lo que aprende. El desarrollo de esta actividad supone que los estudiantes manejan la idea del límite de una función.

Desde esta óptica los saberes matemáticos no se consideran como algo acabado sino como conocimientos en plena creación que se sustentan en una práctica pedagógica como la promovida en la concepción moderna, que por arriba del almacenamiento de conceptos coloca las estructuras conceptuales que se amplían y potencian a lo largo de toda la vida, de modo que no es suficiente con las clases expositivas, sino que deben crearse escenarios donde los alumnos participen en la elaboración de sus propios aprendizajes. En opinión de Gil (op. cit.), esta concepción de la enseñanza debe dirigirse a transformar los programas de actividades, en situaciones problemáticas que carezcan de soluciones obvias, capaces de inmiscuir a los alumnos en un proceso de investigación dirigido por un profesor apto para promover el intercambio de los hallazgos realizados en el aula, a fin de que estos sean reforzados, matizados o cuestionados con base a los conceptos matemáticos existentes.

En este caso, se trata de propiciar un trabajo colectivo de investigación que persigue potenciar y enriquecer la actividad individual y esta labor en opinión de los expertos se desarrolla con una enseñanza de la matemática a través de la solución de problemas, si en esta actividad, el problema es entendido como una situación a partir de la cual se quiere llegar a otra, sin tener un camino seguro para esta travesía, pues esto conduce a la búsqueda de acciones apropiadas para la consecución de esa meta que no es alcanzable de manera inmediata. En este accionar no se excluyen las explicaciones del profesor dirigidas tanto a enriquecer los aportes realizados por los estudiantes como a la conducción del proceso, pero si las actividades, que de manera escrita en el pizarrón reduzcan la participación activa del estudiante y lo coloquen como el receptor de la información proporcionada por el profesor.

Esta concepción de la enseñanza enfocada en la solución de problemas matemáticos deja claro que la aplicación de procedimientos rutinarios para encontrar la solución a un ejercicio, es un proceso distinto a la heurística que ensaya un conjunto de conjeturas en la búsqueda de respuestas al problema que se tiene planteado, pero que no niega el aporte de realizar ejercicios en el aprendizaje de conceptos, propiedades y procedimientos con los cuales puede enfrentarse la tarea de resolver problemas y donde además se tiene claro que la distinción entre ejercicio y problema es una cuestión relativa, pues lo que para una persona constituye un gran reto para otras es sólo un ejercicio rutinario.

Específicamente, en una clase de cálculo para estudiantes de economía, la situación de estimar los costos por unidad, para fabricar una pieza cuyo costo total es C(x) cuando la producción crece de manera desmesurada, es para algunos un reto notable, mientras que para otros es una situación que sólo sugiere el ejercicio rutinario de calcular el límite cuando de la función del costo medio. Desde nuestra perspectiva, son las estrategias desplegadas por el profesor las que ubican el quehacer de la clase en una actividad rutinaria o en la creación de un escenario, donde se aproveche lo que el sujeto ya sabe en la construcción de los conocimientos que están siendo tratados en los problemas que se le plantean.

De acuerdo con Guzmán (1993), la forma de enseñar un tema de matemática siguiendo la estrategia de solución de problemas incluye: una situación problemática de la que surge el tema (basada en la historia, aplicaciones, modelos, juegos…), manipulación por parte de los alumnos, identificación de la situación y sus dificultades, formulación de estrategias posibles, conjeturas diversas de los estudiantes, ataque y resolución del problema, análisis del proceso de solución, prueba de la solución encontrada, generalización hacia nuevos problemas y transferencias de resultados, métodos e ideas.

El maestro que orienta la enseñanza del cálculo en la solución de problemas como herramienta para construir el conocimiento, debe utilizar esta estrategia tanto para justificar y motivar el estudio de un contenido determinado, como para promover el desarrollo de habilidades superiores como consecuencia de haber incitado la resolución de problemas rutinarios que se resuelven a su vez a partir del aprendizaje de conceptos y destrezas matemáticas presentes en los contenidos del tema que se analiza. Por ejemplo, el estudio de los máximos y mínimos en una relación funcional en la clase de economía a la que se ha hecho referencia, puede motivarse invitando a los estudiantes a construir un envase cilíndrico para almacenar una determinada cantidad de líquido a partir de una lámina rectangular, de manera que en su fabricación se utilice la menor cantidad posible de material. Este clásico problema del cálculo, además de convertirse en el escenario heurístico que motive y justifique el estudio del contenido y que en la búsqueda de la solución muestre la necesidad de construir la función que se ajuste a las condiciones del problema y el uso de la derivada como la herramienta que indica la forma de cortar la lámina sin que se desperdicie material en la fabricación del recipiente, enfrenta al estudiante a un proceso parecido al que sigue el matemático activo en la creación de su ciencia y es por tanto el ambiente propicio para fomentar el desarrollo de los procesos mentales que le permitirán desenvolverse en el entorno social.

La enseñanza de la matemática a partir de la solución de problemas, de acuerdo con García (1999), fue planteada en el III Congreso Internacional en Educación Matemática celebrado en Berkeley en 1980, a raíz de las ideas de Freudenthal relacionadas con el estudio de los problemas que se derivan de la enseñanza de la matemática y con la atención de los aprendizajes individuales donde a su parecer se hallan las soluciones a los aparentes fracasos de los estudiantes, junto a las observaciones de Polya quien solicita a los profesores encaminar su actividad docente a mejorar las capacidades intelectuales de sus estudiantes.

Sin embargo, los aportes de Polya ya habían sido presentados en su libro cómo plantear y resolver problemas publicado por Princeton University Press, U.S.A. en 1945, a partir del cual se desarrolla una teoría heurística para la solución de problemas matemáticos, que en un principio se dirigió a la enseñanza básica pero que en la actualidad abarca todos los niveles educativos. Esta teoría se fundamenta en una serie de preguntas e instrucciones que orientan la búsqueda de la solución del problema, en ella se parte de la comprensión del problema dirigida a identificar tanto las incógnitas como las condiciones y la suficiencia de éstas en la búsqueda de la solución, para lo que puede ser útil realizar un posible dibujo o rescribir en otros términos el problema. Continua con la concepción de un plan para resolverlo, donde se incluye las diferencias y analogías de las incógnitas del problema dado con las de otros problemas que se hayan resuelto previamente a fin de poder concebir una estrategia de solución. La ejecución del plan, incluye revisar cada paso de la estrategia para clarificarlos y ver si se pueden probar y, finalmente, se realiza una revisión retrospectiva del problema que además de garantizar la certeza de la solución encontrada abra la posibilidad de encontrar una manera diferente de resolverlo y de aplicarlo a la solución de nuevos problemas. Velasco (2000), describe esta metodología en los términos siguientes una vez que las circunstancias del problema están totalmente claras se proponen varias estrategias, con base en analogía principalmente, en el replanteamiento del problema y en la solución de problemas relacionados que ayuden a resolver el principal. Seguidamente se lleva a cabo el plan seleccionado y se verifica. Finalmente, se analiza la solución para averiguar si se puede obtener de otra forma, y se estudia su utilidad y la del método en la solución de otros problemas.

Entre las ventajas de esta estrategia pedagógica que permite al estudiante manipular los objetos matemáticos para que ejerciten su capacidad mental y adquieran confianza en su propio proceso de aprendizaje, destaca Guzmán (op. cit), el desarrollo de la autonomía de los estudiantes para resolver sus propios problemas, el promover la realización de un trabajo atrayente, divertido, satisfactorio, autorrealizador y creativo, el generar la consolidación de hábitos que van más allá del quehacer matemático y el propiciar una actividad que puede realizarse durante toda la vida.

La fundamentación teórica de la enseñanza a través de la solución de problemas donde se inserta la concepción moderna para la enseñanza del cálculo, puede encontrarse en los aportes del enfoque cognitivo del aprendizaje tanto en la visión norteamericana como en la estructuralista de la psicología europea y en las ideas de Vygotsky (1981) en torno a la forma en que se produce el conocimiento. El primero, en analogía con los modelos de procesamiento de información trata de explicar la forma como las personas procesan la información que reciben del medio de acuerdo a los esquemas mentales existentes en su interior, los cuales le permiten articular la información a través de un proceso de retroalimentación. El segundo, de carácter organicista proveniente de la teoría piagetiana promueve la idea de que el aprendizaje es un proceso de construcción personal que ocurre como consecuencia de la interacción recíproca entre el sujeto y el objeto, en la cual el individuo con sus acciones físicas y cognitivas transforma al objeto y lo organiza en sus marcos conceptuales en un proceso de reconstrucción permanente y la visión de Vygotsky que ve el crecimiento del conocimiento como la interrelación entre el eje del desarrollo orgánico y el eje cultural, que basa el aprendizaje en el proceso de mediación, entendida como la cuantificación de la interacción que se establece entre el sujeto que aprende y el contexto sociocultural que incluye a los organizadores externos, quienes actúan como guías capaces de regular y controlar las actividades o tareas que debe realizar el aprendiz, esto es, la construcción de andamios que lo ayuden a moverse desde lo que sabe hacer hasta el nivel requerido para resolver exitosamente el problema con el que se enfrenta.

Cómo integrar

Los aportes de los enfoques del aprendizaje y las reflexiones acerca de la enseñanza fundamentada en la solución de problemas no niega el papel decisivo de los procesos algorítmicos y de la ejercitación en la consolidación del conocimiento matemático. Por ello, está presente la necesidad de idear escenarios para la enseñanza de la matemática donde se integre competencia, comprensión y estrategia. Ser competente significa poseer destrezas manipulativas o procedimentales para calcular límites, derivadas, integrales o construir la curva de una función; comprender implica establecer las relaciones entre los contenidos y los procesos matemáticos colocados en juego y ser estratégico es poder establecer un auto-gobierno que organice, elabore, repita, controle y evalúe la complementariedad entre la competencia y la comprensión.

Este escenario de acuerdo con Godino (2002), propone una enseñanza de la matemática acorde con los supuestos filosóficos falibilistas que admiten la falibilidad de las ideas que sustentan el conocimiento matemático y se asocian con el pensamiento constructivista de la educación. En tal escenario se distingue el componente práctico que incluye ejercicios, problemas y técnicas de solución; el componente discursivo relacional que hace uso del conocimiento conceptual y argumentativo para generar reglas y justificaciones que encaminen la acción matemática; el componente que integra competencia y comprensión a través de los recursos lingüísticos que se derivan del lenguaje matemático.

Estos ambientes educativos que de manera explícita orientan las actividades que permiten a los estudiantes transformar los materiales de estudio en conocimientos útiles, apuntan hacia la enseñanza estratégica, que en opinión de Monereo (2004), es una praxis docente encaminada a transferir o ceder de manera progresiva a los estudiantes, procesos mentales que les permitan regular sus aprendizajes a través de un conjunto de decisiones, que deben ser ׳intencionales para que no se aparten del objetivo perseguido, conscientes a fin de que los procesos que conducen a la meta perseguida sean objeto de supervisión y regulación continua y sensibles, a las formas en que los estudiantes responden a esos aprendizajes dentro de un contexto donde se incluyen sus conocimientos y las exigencias del proceso de enseñanza. Praxis que a nuestro entender es convergente con el escenario de complementariedad entre el conocimiento para ejecutar operaciones y los procesos heurísticos seguidos en la solución de problemas, que da pie al proceso reflexivo del por qué y para qué se construye del conocimiento matemático en el aula.

Referencias

1. Ausubel, D., Novak, J. y Hanesian, H. (1983). Psicología educativa. Un punto de vista cognoscitivo. México: Trillas.        [ Links ]

2. Artigue, M., Douady, R., Moreno, L., Gómez, P., (1995). Ingeniería didáctica en educación matemática. Un esquema para la investigación y la innovación en la enseñanza y el aprendizaje de las matemáticas. México: Grupo Editorial Iberoamericana.        [ Links ]

3. Beltrán, J. (1993). Psicología evolutiva y de la educación. Madrid: Síntesis.        [ Links ]

4. Carrillo, J. (2000). La formación del profesorado para el aprendizaje de las matemáticas. Revista Uno [Revista en línea], 24. Disponible: http://ocenet.oceano.com/consulta/welcome.do [Consulta: 2004, Diciembre 18]        [ Links ]

5. García, A. (1999). La Didáctica de las matemáticas: una visión general. [Documento en línea]. Red Temática Educativa Europea. Disponible: htt://nti.educa.rcanaria.es/rtee/didmat.html. [Consulta: 2005, Enero 08]        [ Links ]

6. Gil, D. (1993). Enseñanza de las ciencias y la matemática. [Documento en línea]. organización de Estados Iberoamericanos para la Educación, la Ciencia y la Cultura. Disponible: htt://www.campus-oei.org/oeivirt/gil.htm#Intro. [Consulta: 2004, Diciembre 20].        [ Links ]

7. Godino, J. (2002). Competencia y comprensión matemática: ¿qué son y cómo se consiguen?. Revista Uno [ Revista en línea ], 29. Disponible: http://ocenet.oceano.com/consulta/welcome.do [Consulta: 2004, Noviembre 8].        [ Links ]

8. Guzmán, M. de. (1993). Enseñanza de las ciencias y la matemática. [Documento en línea]. organización de Estados Iberoamericanos para la Educación, la Ciencia y la Cultura. Disponible: htt://www.campus-oei.org/oeivirt/edumat.html [Consulta: 2004, Diciembre 20].        [ Links ]

9. Monereo, C. (2004). La Enseñanza Estratégica: Enseñar para la Autonomía. Revista Candidus 27-29, 9-17.        [ Links ]

10. Velasco, A. (2000). El Concepto de heurística en las ciencias y en las humanidades. México: Siglo XXI Editores.        [ Links ]

11. Vera, H y Silva, M. (s.f.). Una propuesta educativa en informática educacional para la enseñanza de la matemática. [Documento en línea]. Disponible: htt://www.sadpro.ucv.ve/agenda/online/vo16n17a0.html. [Consulta, 2005, enero 8]        [ Links ]

12. Vygotsky, L. (1981). Pensamiento y lenguaje. Buenos Aires: La Pléyade.        [ Links ]

Notas:

¹El desarrollo de esta actividad supone que los estudiantes manejan la idea del límite de una función.