Incorporación de la calculadora gráfica en el aula de matemática. Una discusión actual hacia la transformación de la práctica.*

José Ortiz Buitrago

Universidad de Carabobo

Resumen

Se hace una presentación de las nuevas tecnologías, específicamente la calculadora gráfica, y sus usos didácticos; así como los resultados de algunas investigaciones efectuadas en distintos contextos hasta llegar a nuestras propias reflexiones. Se mencionan algunas experiencias realizadas y otras en ejecución, las cuales ponen de manifiesto que la enseñanza de la matemática con el apoyo de nuevos recursos tecnológicos, como la calculadora gráfica, contribuye a fortalecer un proceso natural de comprensión del conocimiento matemático y sus aplicaciones. Se parte de la consideración que el uso adecuado de esas nuevas tecnologías contribuirá a que el profesor de matemática incremente sus competencias didácticas, para hacer más significativos los logros de sus alumnos, cuando diseña y gestiona actividades didácticas que incorporan la calculadora gráfica como uno de sus organizadores. Se recomienda incrementar la investigación como víapara avanzar hacia la incorporación adecuada de la calculadora gráfica u otros recursos didácticosen el aula.

Palabras clave: Nuevas tecnologías, enseñanza de la matemática, formación de profesores de matemáticas, calculadoras gráficas, investigación en educación matemática.

Abstract

Inclusion of the Graphic Calculator in the Teaching of Mathematics. A discussion for the transformation of its practice.

It is a presentation on the didactical use of new technologies, specifically the graphic calculator, as well as the results of some researches in different contexts up until our own reflections. Mention in made of some implemented projects and others in progress, which show that mathematics education with the support of new technological resources, like the graphic calculator, contribute to fortify a natural process of understanding of the mathematical knowledge and its applications. Starting from the consideration that an adequate use of these new technologies will contribute to an increase of the Mathematics teacher didactical skills that will make the student´s achievements more meaningful when he designs and manager didactical activities that involve the graphic calculador as one of its organizers. It is recommended to increase research, advance towards a suitable incorporation of the graphic calculator or other didactic resources in the classroom.

Key words: New Technologies, Mathematics Teaching, Mathematics Teachers Training, Graphic Calculator, Research in Mathematics Education.

* Recibido: febrero 2006.

Aceptado: septiembre 2006.

Introducción

La idea de sociedad global ha significado un acercamiento a las nuevas tecnologías y cambios a distintos ámbitos de la sociedad. En particular, en la Educación, las nuevas tecnologías se han ido incorporando como un recurso al cual, cada vez más, recurren los docentes. A estos cambios no ha estado ajena la didáctica de la matemática, donde el uso de nuevos recursos en la enseñanza y aprendizaje ocupa el interés de educadores e investigadores en diferentes países. Un campo particular de atención ha sido la formación del profesor de matemáticas para el desempeño en el ambiente de las nuevas tecnologías, así como la conformación de una infraestructura dentro de ese nuevo contexto.

Lo planteado en el párrafo anterior ya ha sido considerado por sociedades de profesores y por diversos organismos internacionales. Por ejemplo, The National Council of Teachers of Mathematics recomienda el uso extensivo de calculadoras y computadoras en todos los niveles educativos (NCTM, 2000). Asimismo, la organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura (UNESCo) recomienda a los gobiernos su uso, argumentando que las nuevas tecnologías brindan una posibilidad sin precedentes y que aportan grandes ventajas en el plano pedagógico (Delors, 1996).

En el contexto de la Educación Matemática tiene particular interés el estudio del aprendizaje y la enseñanza de conceptos matemáticos y sus relaciones, a manera de lograr que cada individuo pueda comprender mejor su mundo fenomenológico y alcanzar los niveles de conocimiento necesarios para desenvolverse en la sociedad presente y futura. La aparición del computador ha permitido avanzar, en distintas esferas de la vida del hombre, hasta límites insospechados hace algunos años. Se ha ido pasando del cálculo numérico al cálculo simbólico, lo cual ha dado como resultado un cambio del abordaje de los problemas matemáticos pues, ahora por ejemplo, se puede hacer más hincapié en el aprendizaje de conceptos y comprensión de los problemas, debido a la rapidez de ejecución de cálculos complejos, que restaban tiempo a la comprensión de conceptos e ideas involucradas en la resolución de problemas. Por otra parte, la forma de adquirir los conocimientos también ha cambiado con la interacción estudiante-tecnología; es decir, el alumno introduce expresiones simbólicas en lenguaje matemático y sus respuestas son dadas siguiendo los mismos códigos y de acuerdo a lo esperado, también escrito de la misma manera simbólica que lo propuesto.

Es muy importante reconocer que el uso y manejo de las tecnologías conlleva ciertas responsabilidades tanto éticas como del conocimiento de su utilización y funcionamiento. En cuanto a lo ético las tecnologías por si solas no son ni buenas ni malas, depende de la manera como el hombre les dé uso racional y productivo. Tampoco son la panacea, ni la antítesis del espíritu humano, son una herramienta para contribuir a la comprensión del mundo y a la indagación y profundidad de las cosas, elementos o situaciones. La potencia de la tecnología puede ayudar a los estudiantes a desarrollar comprensión y aplicación de conceptos matemáticos.

Son muchos los autores que sostienen que el uso de la tecnología en la clase de matemáticas es uno de los tópicos que ha generado más atención entre los educadores matemáticos de diferentes niveles educativos. También hay quienes consideran que los profesores de matemáticas pueden cambiar su papel de "poseedores" del conocimiento a motivadores del aprendizaje, con lo cual contribuyen a proporcionar a los alumnos la base necesaria para comprender y relacionar los nuevos conocimientos con los ya adquiridos (Novak y Gowin, 1988). Sin embargo, a pesar del avance tecnológico y la aparición de nuevas tecnologías con alta potencialidad didáctica, encontramos que los profesores son formados, en la mayoría de las universidades, con metodologías basadas en la explicación mediante clases magistrales.

La reflexión sobre la enseñanza de las matemáticas no debe estar ajena a las implicaciones y uso de las nuevas tecnologías en la formación de los profesores de matemática, desde su acercamiento necesario como usuarios hasta la utilizacióncomo recurso didáctico. En relación a la función didáctica, se debe tener presente que las nuevas tecnologías no sustituyen al profesor en el proceso de enseñanza, sino que le plantea nuevos retos y le exige nuevas competencias.

De ahí el énfasis en el conocimiento profesional del profesor de matemáticas, que le aporte opciones para utilizar y valorar un mayor número de materiales y recursos, determinar y establecer las secuencias metodológicas a incorporar en el aula y reforzar los conceptos y procedimientos matemáticos que le sugieran nuevas formas de evaluar e interactuar con los alumnos. En Venezuela la poca atención a la formación didáctica específica del profesor de matemáticas, lo induce a recurrir en su campo profesional al ensayo y error como el principal instrumento para aprender a enseñar (Marcelo, 1992). Una manera de contribuir a superar esta limitación sería el acercamiento de los profesores en formación a las nuevas tecnologías, lo cual podría inducir cambios enel desempeño de su futura actividad profesional con la incorporación de nuevos dominios de enseñanza que harían mucho más fecundo el proceso de aprendizaje de las matemáticas.

La incorporación de las nuevas tecnologías en educación es objeto de interés en diferentes ámbitos. Desde la educación matemática se han realizado esfuerzos para su inclusión en el currículo de una manera sistemática y congruente con las necesidades escolares actuales, de tal manera que se avance en el logro de un aprendizaje significativo de las matemáticas. Esta idea es compartida por Kaput (1992) y Galbraith & Haines (1998, 2001) para quienes las nuevas tecnologías informáticas tienen un impacto potencial sobre la comprensión de las matemáticas por parte de los alumnos. Sin embargo, la utilización de las nuevas tecnologías en el proceso de enseñanza y aprendizaje de las matemáticas es objeto de controversia, desde los que sostienen que su empleo únicamente trivializa los procesos de enseñanza y aprendizaje hasta los que argumentan, por el contrario, que introduce una complejidad exacerbada en la actividad del docente y del alumno. Para autores como Trouche (2000, 2005) la introducción de la tecnología no simplifica el trabajo del profesor ni del estudiante, sino que requiere la construcción de una enseñanza compleja y un ambiente de aprendizaje adecuado. Asimismo, este autor agrega que el ambiente con las calculadoras necesita ser construido por los profesores, de manera que potencien en sus alumnos actitudes favorables y una mejor relación con el conocimiento matemático. Si dichos recursos no son utilizados adecuadamente pueden llegar a ocultar más que iluminar las matemáticas en las situaciones del mundo real (Blum y Niss, 1991).

Uno de los proyectos en marcha, dirigidos a la inclusión de las nuevas tecnologías en los currículos, es el reportado por Usiskin (2000), director del University of Chicago School Mathematics Project (UCSMP), donde afirma que si se evita la incorporación de la tecnología, condenamos a los alumnos al desconocimiento de gran parte de las matemáticas. Por este motivo, en el UCSMP se contempla la utilización de computadores y calculadoras, admitiendo que éstos no solo condicionan la aproximación al estudio del contenido matemático, sino también al contenido en sí mismo. En el UCSMP, los profesores y alumnos consideran variaciones de enfoques en los problemas, prueban conjeturas, procesan grandes masas de datos, dibujan figuras geométricas precisas y representan los conceptos de maneras diferentes.

En general, son muchos los retos y las expectativas que se abren con la incorporación de las nuevas tecnologías en la enseñanza y aprendizaje de las matemáticas, uno de ellos está en la formación de docentes con el dominio didáctico que les permita el aprovechamiento de las nuevas tecnologías como recursos, tanto en la planificación como en la gestión de las actividades didácticas a desarrollar con sus alumnos, con un sentido innovador y crítico.

Calculadoras gráficas en el aula 

El auge de las calculadoras en educación matemática ha ido perfilándose en diferentes direcciones. La calculadora, desde su aparición, ha generado inquietudes tanto en el ámbito docente como de investigación. Según Dick (1992) si se utiliza la calculadora gráfica en la escuela, ocurrirá un redireccionamiento del currículo hacia una disminución del cálculo numérico y simbólico, lo cual favorecerá la profundización en el aprendizaje conceptual. En ese mismo sentido, Dunham y Dick (1994) afirman que la disponibilidad de calculadoras gráficas ha motivado a reexaminar el cómo enseñar matemáticas. Es decir, para los autores, las calculadoras gráficas pueden facilitar cambios en los roles de los alumnos y de los profesores en el aula, resultando unos ambientes de aprendizaje con mayor interactividad y exploración. En ese sentido, la calculadora gráfica puede ser un catalizador y no un obstáculo en el aprendizaje de las matemáticas.

Dunham y Dick (1994), se preguntan si la calculadora gráfica es sólo para confirmar resultados obtenidos con papel y lápiz, o, para incentivar la exploración y la investigación. Agregan que la sola presencia de la calculadora gráfica no determina su uso, por ejemplo, para relacionar gráficos con sus ecuaciones, interrelacionar sistemas de representación, entre otras acciones de índole cognitiva. Para estos autores la resolución de problemas se puede mejorar porque: 1) las calculadoras gráficas dan más tiempo para la instrucción mediante la reducción de atención a la manipulación algebraica, 2) las calculadoras gráficas suministran más herramientas para la resolución de problemas, especialmente para estudiantes con poca fortaleza en habilidades algebraicas, y 3) los alumnos perciben la resolución de problemas de una manera distinta, concentrándose en la comprensión del problema y en el análisis de la solución.

En cuanto a las necesidades futuras, Dunham y Dickse preguntan acerca de cuáles son las habilidades con papel y lápiz que siguen siendo importantes con la incorporación de la calculadora gráfica. Sobre este último aspecto, Herget, Heugl, Kutzler y Lehmann (2000), se preguntan ¿qué habilidades manuales de cálculo con papel y lápiz necesitan los alumnos cuando utilizan calculadoras gráficas?. Estos autores parten del hecho que los sistemas de cálculo simbólico1 (CAS), en particular las calculadoras gráficas, llegarán a ser una herramienta estándar para enseñar y aprender matemáticas. En su artículo, consideran que más importante es la distinción entre las metas del "resolver una operación" (que puede ser relegado a una calculadora) y "elegir una estrategia" (que no puede ser hecho por un calculador).

Los autores presentan una lista de hechos para los cuales indican cuando se requiere usar tecnología y cuando no es necesario. Asimismo, muestran situaciones donde tienen duda para decidir entre el uso o no de tecnología. Al respecto, en el cuadro 1, a manera de ejemplo, Herget et al (2000) proponen algunos hechos relativos a los temas de ecuaciones e inecuaciones.

Cuadro 1

Del cuadro 1 se podría deducir que las ecuaciones de la forma ax+b=c donde a, b y c son parámetros fijos, los alumnos deberían realizarlas sin acudir a la tecnología, mientras que se debería acudir a la tecnología para resolver las ecuaciones de la forma ax+b=cx+d, donde a, b, c, d son parámetros fijos. No se presentan casos de situaciones de duda para utilizar o no la tecnología. Respecto a la resolución de la ecuación x+1=x+1 se espera que los alumnos la desarrollen sin tecnología. Por otra parte, se presenta duda entre usar o no la tecnología con el caso de la ecuación 2(x+1)=2x+2. No se presentan casos de esta naturaleza para ser resueltos con el empleo de la tecnología.

Para el caso de las inecuaciones, podríamos afirmar que los autores proponen que x+a<b, con a, b parámetros fijos, se debería resolver sin utilizar la tecnología. Hay dudas para emplear o no la tecnología en la resolución de las inecuaciones del tipo x+a<x+b con a, b parámetros fijos. En el caso de las inecuaciones de la forma ax+b<cx+d con a, b, c, d hay recomendación de utilizar la tecnología. Finalmente, del último caso presentado por los autores, en el cuadro 1, podríamos concluir que las inecuaciones de la forma x<x+a con a fijo se debería desarrollar sin tecnología. Para las inecuaciones en x de la forma ax<b donde a es un parámetro fijo y bΡ se recomienda emplear la tecnología. No se presentan hechos que evidencien duda sobre el uso o no de la tecnología.

Con estos planteamientos los autores pretenden fundamentalmente provocar a los investigadores sobre el tema de las habilidades que deben permanecer cuando se usa tecnología CAS, lo cual también es aplicable al caso de las calculadoras gráficas. Ese es un tema de particular interés cuando se diseñan actividades didácticas con la incorporación de la calculadora, para dar un uso más adecuado a la tecnología. Recomendaciones en ese sentido ayudarían a fortalecer las competencias didácticas de los profesores de matemáticas en formación (Fey, Cuoco, Kieran, McMullin y Zbiek, 2003).

Actualmente en países de América y Europa se está favoreciendo su utilización. Por ejemplo, las calculadoras gráficas (no simbólicas) están permitidas, a nivel oficial, en los exámenes en Inglaterra, Francia, Escocia, Suecia, Noruega y Finlandia. Y los sistemas de cálculo simbólico lo están en Escocia y Francia. Además, en Portugal, Francia, Austria y Eslovenia el Estado recomienda y apoya el uso de sistemas de cálculo simbólico en la enseñanza.

Para Kutzler (2000, 2003), las calculadoras gráficas permiten hacer énfasis en la visualización, experimentación y concentración lo cual tiene implicaciones curriculares importantes; en particular la graficación incrementa la importancia de desarrollar comprensión sobre las escalas utilizadas en los ejes y la transformación de gráficos. Esto también fue estudiado antes por Leinhardt, Zaslavsky y Stein (1990) quienes al respecto afirman que las tareas relacionadas con la escala cobran más importancia cuando se usan tecnologías gráficas.

Berry y Francis (2000), en sus investigaciones realizadas en Inglaterra, concluyeron que el uso de la calculadora gráfica mejora las habilidades de investigación matemática de los estudiantes y en consecuencia les ayuda en la resolución de problemas del mundo real. En este mismo sentido, los autores sostienen que en estos ambientes de aprendizaje los estudiantes empiezan a formularse preguntas que revelan el inicio de la comprensión de los conceptos matemáticos.

El uso de la calculadora gráfica en la enseñanza de las matemáticas tal como ya se ha señalado anteriormente, expresa la presencia de las nuevas tecnologías en el aula de matemáticas. Por supuesto, tiene sus ventajas y también sus limitaciones. Algunas limitaciones se ubican en la precisión de los cálculos (alcance de la manipulación simbólica), la graficación de ciertas funciones y el uso inadecuado en operaciones que no lo requieren entre otras. Las ventajas están asociadas con su potencialidad simbólica y gráfica (desde el nivel escolar primario hasta el superior). En particular, la calculadora gráfica TI-Voyage 200 permite transformar expresiones, simplificar o resolver ecuaciones y modelizar situaciones problema; éste último conlleva la realización de experimentos, formulación y comprobación de conjeturas; además permite la investigación y exploración de las conexiones entre distintas representaciones de un concepto o de una situación problema. Esta calculadora tiene incorporada una versión del programa Derive. Esto caracteriza a la calculadora gráfica como un recurso de alta potencialidad para aprender y enseñar matemáticas.

Waits (2000, p.200), al referirse a la calculadora gráfica, señala que "...nuestro mundo de la enseñanza y aprendizaje de las matemáticas no volverá a ser el mismo...existe una nueva herramienta que hace posible y práctica la visión del currículo matemático mejorado, basado en la tecnología informática...". La calculadora gráfica tal como ya se ha señalado anteriormente, representa la presencia de las nuevas tecnologías en el aula de matemáticas. Por supuesto, tiene sus ventajas y también sus limitaciones. Algunas limitaciones se ubican en el terreno del nivel de precisión de los cálculos (alcance de la manipulación simbólica), la graficación de ciertas funciones y el uso inadecuado en operaciones que no lo requieren entre otras. Las ventajas están asociadas con su potencialidad simbólica y gráfica (desde el nivel escolar primario hasta el superior).

La necesidad de actuar de manera efectiva y eficiente en el proceso educativo ha dirigido la atención hacia la formación de los profesores en el empleo didáctico de las calculadoras gráficas. A tal efecto, Waits y Demana (1998), consideran que el profesor de matemáticas es el componente más valioso para la incorporación de las calculadoras en la enseñanza y aprendizaje de las matemáticas. Estos investigadores opinan que no se puede esperar cambios fundamentales en sus métodos de enseñanza si no han sido introducidos en el uso de estos recursos, a los cuales reconocen como un importante agente de cambio. Esto queda resaltado cuando se afirma que el uso efectivo de la tecnología en el aula de matemáticas depende del profesor (NCTM, 2000), para lo cual se asume que éste debe tener una formación adecuada en el manejo técnico y didáctico de la tecnología que incorpore en su actividad docente. En ese sentido, los Estándares del NCTM (2000) refieren que la tecnología no es una panacea y que su uso efectivo depende del profesor de matemáticas.

En la década de los 80, con el informe Cockcroft (1985), se sugiere la necesidad de contar con materiales que orienten a los profesoressobre las maneras de incorporar las calculadoras en la enseñanza de las matemáticas. Recientemente, Hilton (2000), afirma que la calculadora tiene una influencia sobre lo que se enseña y sobre el cómo enseñamos. Para este autor, con la CG, los profesores podrían eliminar tanto la monotonía en aritmética elemental, como las manipulaciones simbólicas del álgebra y del cálculo infinitesimal, de tal manera que se pueda dar más énfasis a la construcción de modelos matemáticos surgidos de situaciones del mundo real. De ahí que, el rol del profesor contemplaría crear situaciones de interés que contribuyan al surgimiento de conceptos y relaciones matemáticas (Ruthven, 1992).

Algunas implicaciones de la incorporación de la calculadora en la formación del profesorado son puestas en evidencia en el estudio desarrollado por Bitter y Hatfield (1992), sobre la implementación de calculadoras en educación secundaria en Arizona State University (USA). En el mismo se partió del hecho que las experiencias de aprendizaje de las matemáticas deberían estar diseñadas para "enganchar" a los profesores participantes en una forma de trabajo directa y dinámica cuando participaban como alumnos en un ambiente de aprendizaje colaborativo. En cada actividad, los participantes intercambiaban ideas y compartían estrategias de enseñanza y además discutían sobre problemas y soluciones relacionadas con el uso de la calculadora. Los autores encontraron que los profesores participantes estarían dispuestos a poner en práctica un currículo que tuviese integradas actividades bien planificadas y diseñadas con la calculadora.

Conocimiento del profesor

El interés por el qué aprende el profesor y cómo superar la dualidad existente entre la formación conceptual y teórica y la formaciónpráctica en el servicio docente plantea el problema de la formación inicial de cara a la formación profesional, para que los profesores en formación logren las competencias necesarias para desempeñarse adecuadamente en su futuro trabajo profesional (Ensor, 2001; Adler, Ball, Krainer, Lin y Novotna, 2005).

El conocimiento que cada profesor de matemáticas debe adquirir en su formación inicial, para lograr la competencia que le permita desarrollar su función eficientemente, involucra un dominio disciplinar y un conocimiento didáctico. Es decir, además de los conocimientos matemáticos que adquiere en su formación inicial, el profesor de matemáticas requiere de otros conocimientos relativos a la enseñanza y el aprendizaje de las matemáticas, que le ayudarán a conformar su competencia profesional. Esto significa reconocer la necesidad, entre otras, de dotar al profesor de habilidades y destrezas para: planificar programas de matemáticas escolares, diseñar actividades didácticas, establecer dificultades y obstáculos, diagnosticar y prevenir errores, conducir y evaluar el aprendizaje de los alumnos, enseñar conceptos o procedimientos matemáticos, evaluar innovaciones, reflexionar sobre su actuación y, en general, comprender su papel en la escuela. Ese nivel de preparación del profesor de matemáticas estaría en relación directa con la comprensión matemática y el logro de los alumnos. Todo lo anterior, junto con el conocimiento matemático y las destrezas y conocimiento práctico para la gestión de grupos de alumnos, forma parte relevante de lo que llamamos conocimiento profesional del profesor de matemáticas o, simplemente, conocimiento del profesor de matemáticas.

La competencia es la disposición de conocimiento o habilidades de una persona para realizar apropiadamente una actividad (Short, 1985). De esta manera, la competencia implica elegir y conocer el por qué uno elige hacer lo que hace. Así que, entendemos por competencia didáctica la capacidad para seleccionar con criterio fundado un conocimiento particular y/o habilidades para aplicarlas en la situación de enseñanza que se considere pertinente. Esa capacidad de selección requiere de ciertos conceptos básicos para dar inicio a la reflexión y toma de decisiones en el proceso de enseñanza.

Desde nuestra perspectiva el conocimiento del profesor involucra competencias didácticas que contribuyen a que el docente asuma otras alternativas de enseñanza tales como conectar las matemáticas con ellas mismas; es decir, relacionar unos conceptos con otros, representar de diferentes maneras un mismo concepto, probar regularidades y hacer generalizaciones en caso de que sean posibles. Por otra parte, también el profesor puede hacer uso de la matematización, o sea, pasar del mundo físico y social (mundo real) al mundo de los símbolos para abordar y tratar matemáticamente situaciones problema. En la referida matematización se dan procesos que conducen a identificar las matemáticas en otros contextos, formular y visualizar problemas de diferentes maneras y descubrir relaciones y regularidades, entre otros. Con la matematización se le presenta la oportunidad de relacionar las matemáticas con otras ciencias y con la vida cotidiana. Cuando el profesor tiene competencia didáctica puede sacar mayor provecho de la matematización en la enseñanza de las matemáticas. Es decir la competencia didáctica es un elemento clave en el proceso de enseñanza de las matemáticas.

El conocimiento que el profesor de matemáticas adquiere durante la formación inicial, podría favorecer la sensibilización de los futuros profesores ante las innovaciones y estimular los deseos de mejora permanente de su actividad, una vez que se encuentren en su campo profesional. Esto significa que la formación inicial recibida podría evitar situaciones como la incomodidad de enfrentarse en el aula con un ambiente caracterizado por las innovaciones tecnológicas para la enseñanza, es decir con el uso de tecnologías informáticas en la enseñanza y aprendizaje de las matemáticas. En efecto, en un informe sobre la educación secundaria en Canadá, los resultados de una encuesta aplicada a profesores de matemáticas revelaron que éstos no utilizan las herramientas de nuevas tecnologías, exigidas en el nuevo plan de estudios, porque las mismas no están disponibles o porque los profesores no sienten confianza al utilizar la tecnología (Brown y Rushowy, 2001).

En este sentido, pensar en un conocimiento profesional del profesor de matemáticas significa considerar conocimientos que le aporten opciones para utilizar y valorar un mayor número de herramientas conceptuales, que le permitan determinar y establecer las secuencias metodológicas para presentar y reforzar los conceptos y procedimientos matemáticos y le sugieran nuevas formas de evaluar e interactuar con los alumnos.

Una parte del conocimiento profesional de los profesores lo constituye su conocimiento didáctico. El conocimiento didáctico es el conocimiento necesario para la planificación, puesta en práctica y valoración de actividades didácticas o más en general de unidades didácticas. Es decir, el conocimiento didáctico del profesor de matemáticas se manifiesta en la competencia para el diseño, desarrollo y evaluación de unidades didácticas. Las unidades didácticas constituyen, probablemente, una de las tareas más importantes e interesantes que deben realizar los profesores, ya que en ellas se plasman sus ideas, enfoques y valores con respecto a su materia. Además, ésta es una tarea dinámica susceptible de mejora o cambio, que implica la constante reflexión e indagación de los profesores sobre las matemáticas escolares y sobre su labor educativa fundada en su enseñanza y aprendizaje.

Esto significa que la unidad didáctica, junto a las actividades didácticas que la conforman, debe ser una verdadera guía de organización y actuación para el docente, en cuanto a la selección, secuencia y estructura de las actividades a desarrollar en el tiempo así como respecto a los objetivos pretendidos en el proceso de enseñanza y aprendizaje. En esa concreción de las unidades didácticas es donde se hace evidente la necesidad de un conocimiento que lo sustente, el conocimiento didáctico, soportado en los organizadores del currículo, y sus manifestaciones en competencias didácticas. Es allí donde el futuro profesor de matemáticas inicia su aprendizaje práctico para su futuro desempeño profesional.

En la figura 1 se sintetiza la relación entre el conocimiento didáctico y las unidades didácticas. En la misma se observa que la didáctica de la matemática ofrece al futuro profesor herramientas conceptuales que requiere para alcanzar el análisis de los conocimientos de las matemáticas escolares y con ello planificar y gestionar sus actividades didácticas. Esas herramientas están vinculadas con tres bloques identificados por el currículo, los fundamentos de las matemáticas escolares y los organizadores del currículo. Estos últimos constituyen la base para realizar el análisis didáctico que se concretará con la elaboración de una actividad didáctica o de una unidad didáctica completa. Cuando se realiza el análisis didáctico, dichas herramientas actúan de manera conjunta y simultánea. Esto ayudaría, en la medida que el profesor de matemáticas adquiera mejor formación, para minimizar la brecha o diferencia entre el currículo de su plan de formación como profesor y lo que él tiene que enseñar a los alumnos en la escuela. En particular los organizadores del currículo de matemáticas (Rico, 1997; Ortiz, Rico y Castro, 2007) son nociones que, entre otras peculiaridades, ayudan a la búsqueda de relaciones entre los conceptos matemáticos y de éstos con el mundo físico, natural y social así como a comprender el uso de diferentes recursos y representaciones para incrementar la comprensión de las matemáticas escolares.

Figura 1. Relación entre el conocimiento didáctico y las unidades didácticas 

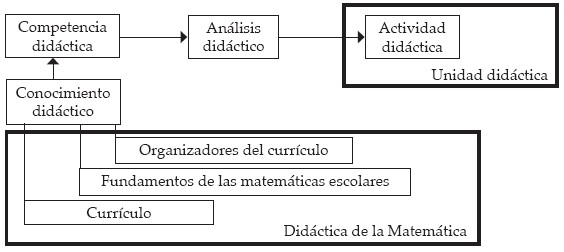
Algunas experiencias con nuevas tecnologías en el aula de matemática

Super (1992), revisa la puesta en práctica de tres innovaciones, en los Estados Unidos, que incorporan el uso de las calculadoras. El autor considera dentro de las recomendaciones para los profesores: 1) que las calculadoras sean utilizadas por los alumnos, para realizar cálculos difíciles, relacionados con aplicaciones a la vida real; 2) que las calculadoras no reemplacen la necesidad de hacer uso de las habilidades con papel y lápiz; entre otras. Finalmente, el autor afirma que cuando las estrategias de implementación son serias y bien empleadas, las calculadoras pueden llegar a ser parte integrante del currículo de las matemáticas escolares.  

Mohammad (1999) plantea que preparar a los profesores de matemáticas en formación, en el uso de nuevas tecnologías, tiene dos ventajas: 1) los profesores no sentirán aprensión al utilizar la tecnología en sus aulas , y 2) pueden ayudar en la formación tecnológicade sus colegas en servicio en los centros educativos. A partir de su experiencia con 28 estudiantes de educación matemática (University of Illinois at Urbana-Champaign), logró que las competencias en manejo de las calculadoras gráficas, y en otras herramientas tecnológicas como hojas de cálculo, procesadores de textos y construcción de páginas web, mejoraran significativamente. Concluyó que, más que la integración de la tecnología en la formación del profesor de matemáticas, es necesario el trabajo con experiencias de aprendizaje sólidas que incorporen la tecnología. En síntesis, plantea que los programas que se dicten a los profesores en formación deben dirigirse a la adquisición de competencias en tecnología, relacionadas con su futuro campo profesional, buscando los grados de aprovechamiento del programa, en cuanto a las habilidades y destrezas para la enseñanza de las matemáticas con tecnología.

Acerca de la evaluación del aprendizaje de los alumnos, con el uso de la calculadora gráfica, Anderson, Bloom, Mueller y Pedler (1999), Ruthven (2002) y Ball y Stacey (2003) proponen algunos cambios tales como la preparación cuidadosa de las actividades de evaluación, por ejemplo analizar gráficas de funciones en lugar de solamente trazarlas, es decir acudir a estudios cualitativos de las funciones. Kissane, Kemp y Bradley (2000) afirman que el uso de la calculadora gráfica debe integrarse en todos los aspectos del currículo, lo cual implica su incorporación en las actividades de evaluación tales como tareas, pruebas, y exámenes. Los autores informan que de esta manera fue como los alumnos participantes en sus investigaciones dieron importancia al trabajo con dicha calculadora y, además, fueron dando un uso adecuado en el sentido que decidieron cuándo usarla e interpretar los resultados obtenidos, tanto para describirlos matemáticamente, como para contrastarlos con situaciones problema.

Berry y Francis (2000), en sus investigaciones realizadas en Inglaterra, concluyeron que el uso de la calculadora gráfica mejora las habilidades de investigación matemática de los estudiantes y, en consecuencia, les ayuda en la resolución de problemas del mundo real. En este mismo sentido, los autores afirman que en estos ambientes de aprendizaje los estudiantes empiezan a formularse preguntas que revelan el inicio de la comprensión de los conceptos matemáticos. Sin embargo, Streun, Harskamp y Suhre (2000), mantienen que el uso de la calculadora gráfica por períodos cortos no es suficiente para establecer un sólido conocimiento y comprensión de las matemáticas. Concluyen estos autores que se hace necesario usar la calculadora gráfica en períodos largos de tiempo para mejorar los logros de los alumnos en matemáticas. Además, agregan que los alumnos con preferencia por soluciones gráficas pueden ganar con el uso de la calculadora, mientras que, los que tienen preferencia por soluciones algorítmicas usarán con menos frecuencia la calculadora para resolver problemas.  

Hitt (2000) en las experiencias realizadas en México con profesores de matemáticas de escuela secundaria ha encontrado razones a favor y en contra para el empleo de la tecnología en la enseñanza y aprendizaje de las matemáticas, específicamente para las calculadoras gráficas. Dentro de los aspectos positivos se mencionan la posibilidad de visualización de los resultados de procesos algebraicos, la manipulación simbólica permite la concentración en tareas de mayor complejidad que promueven más aprendizaje conceptual, y el incremento del interés en el aprendizaje de las matemáticas. Los aspectos negativos se refieren a que la tecnología trivializa algunos problemas y los transforma en ejercicios rutinarios, promueve la búsqueda de respuesta a los problemas mediante el método de ensayo y error y, las representaciones gráficas inhiben el pensamiento analítico. El trabajo de este autor resulta de interés puesto que se realiza con profesores, aunque no especifica si en el grupo han participado profesores en formación.

Los principios y estándares para las matemáticas escolares (NCTM, 2000) otorgan suma importancia a la incorporación de la tecnología en la transmisión y comprensión del conocimiento matemático. El principio referido a la tecnología establece que la misma es esencial en la enseñanza y aprendizaje de las matemáticas, que influye en las matemáticas que se enseñan y que potencian el aprendizaje de los estudiantes. En cuanto a las calculadoras, se dice que éstas pueden ayudar a los alumnos a examinar más ejemplos o formas de representación que podrían realizarse con papel y lápiz, dejando la posibilidad de hacer y explorar conjeturas con mayor facilidad. En general, debido a las bondades de las calculadoras, los estándares recomiendan su utilización extensiva en el aula de matemáticas. Por supuesto, no se obviará que aunque muchas destrezas pasarán a ser obsoletas, otras seguirán siendo necesarias para las actividades relacionadas con las matemáticas, tal es el caso del cálculo mental (Waits y Demana,1996).

Bedoya (2002) realizó una investigación evaluativa sobre la enseñanza de funciones con la utilización de calculadora gráfica. En los resultados del estudio, efectuado con profesores de matemáticas en formación, se destaca la caracterización de tres tipologías de futuros profesores estructuradas a partir de rasgos actitudinales relacionados con el programa implementado. En la primera de ellas se incluye el grupo de profesores que se caracteriza por su carácter reflexivo, innovador, autónomo y efectivo frente al uso de la calculadora gráfica en la enseñanza de las matemáticas; es decir, aquellos que muestran actitud favorable al acceso y adaptación de nuevas propuestas tecnológicas en la enseñanza de las matemáticas. El segundo tipo identificado se caracteriza por ser aquiescente y poco autónomo frente a las nuevas propuestas tecnológicas; es decir, aquellos que presentan actitud favorable hacia el uso de las tecnologías pero no muestran efectividad al llevar a la práctica sus intenciones favorables. El tercer tipo se caracteriza por manifestar resistencia a la innovación tecnológica, y presentar una actitud desfavorable hacia la CG; es decir, en este último tipo se agrupa aquellos futuros profesores que se manifiestan explícitamente en contra de las CG a pesar de reconocer su utilidad. Los sujetos de esta tipología opinan que las calculadoras gráficas son "...’peligrosas’ y problemáticas como recursos para la enseñanza y aprendizaje con estudiantes de secundaria" (p.434). Este estudio propone indagar acerca del cómo actuar, en las dos últimas tipologías, para contribuir a la integración y al cambio de actitud favorable hacia las nuevas tecnologías en el currículo de matemáticas.

En sus trabajos con profesores en formación, ortiz (2000, 2002) encuentra que los participantes muestran dominio de comandos, técnicas y utilidades para utilizar la calculadora gráfica como una hoja de cálculo e introducir las variables y funciones algebraicas, lo cual abre otra forma de abordaje para los problemas algebraicos. Por otro lado, ortiz (2004), indaga respecto a las competencias didácticas de preparadores de matemáticas cuando participan en la implementación de un programa que incorpora las representaciones y la calculadora gráfica en el diseño de actividades didácticas relacionadas con las matemáticas del primer año de universidad en una facultad de ciencias económicas y sociales. Los preparadores muestran capacidad para incorporar nuevas competencias didácticas en el uso de los sistemas de representación y la calculadora gráfica para el proceso de enseñanza y aprendizaje de la matemática. Los preparadores ponen en evidencia dominio para integrar en la dinámica de enseñanza los sistemas de representación y el uso de la calculadora gráfica.

Reflexiones finales 

Cada día es más evidente la necesidad de contar con profesores de matemáticas que posean, no sólo los conocimientos matemáticos, sino también conocimientos didácticos para afrontar los procesos de enseñanza y aprendizaje que se generan durante la relación docente alumno en el aula. En consecuencia, es muy importante la puesta en contacto de los profesores con programas de formación dirigidos a fortalecer su formación didáctica con la incorporación de nuevas tecnologías, en particular la calculadora gráfica (CG); es decir, hacer propuestas innovadoras de diseño y elaboración de actividades didácticas con calculadoras gráficas para favorecer su competencia didáctica.  

En ese sentido, se justifica la incorporación del empleo didáctico de la CG debido a que son los profesores de matemáticas los llamados a impulsar la incorporación de la calculadora en la enseñanza y aprendizaje de las matemáticas. En consecuencia, actuar en el ámbito de la formación inicial y permanente favorece la familiarización de los profesores con las nuevas tecnologías y puede contribuir a fomentar el uso de la misma en los centros educativos.

El empleo de nuevas tecnologías en la enseñanza y el aprendizaje de las matemáticas se verá favorecido en la medida que se tienda a profundizar y desarrollar investigaciones que involucren propuestas didácticas con la incorporación de esos recursos. En ese sentido, los resultados de las investigaciones deben llegar a los potenciales usuarios de tal manera que ellos encuentren pautas acerca de las posibilidades y limitaciones para su utilización en el aula. Es una tarea que deben abordar los investigadores a la vez que se incrementa la investigación matemática con su respectiva divulgación. Estas acciones ayudarán a transformar la práctica de estudiantes y docentes de matemáticas hacia una educación matemática de calidad.

Referencias 

1. Adler, J., Ball, D., Krainer, K., Lin, F. y Novotna, J. (2005). Reflections on an Emerging Field: Researching Mathematics Teacher Education. Educational Studies in Mathematics, 60, 359-381.         [ Links ]

2. Anderson, M., Bloom, L., Mueller, U. & Pedler, P. (1999). The impact of the graphics calculator on the assessment of calculus and modelling. International Journal Mathematics Education Science and Technology, 30(4), 489-498.        [ Links ]

3. Ball, L. y Stacey, K. (2003).What Should Students Record When Solving Problems with CAS?. En J. Fey, A. Cuoco, C. Kieran, L. McMullin y R.M. Zbiek (Eds.), Computer Algebra Systems in Secondary School Mathematics Education. Reston, VA, USA: National Council of Teachers of Mathematics.        [ Links ]

4. Bedoya, E. (2002). Formación Inicial de Profesores de Matemáticas: Enseñanza de Funciones, Sistemas de Representación y Calculadoras Gráficas (Tesis Doctoral). Granada: Universidad de Granada.         [ Links ]

5. Berry, J. y Francis, B. (2000). Descubrir las matemáticas avanzadas a través de actividades con calculadoras. En P. Gómez y B. Waitts (Eds.), Papel de las calculadoras en el salón de clase. pp.3-14. Bogotá: una empresa docente.        [ Links ]

6. Bitter, G. y Hatfield, M. (1992). Implementing Calculators in Middle School Mathematics: Impact on Teaching and Learning. En J. Fey & C. Hirsch (Eds.), Calculators in Mathematics Education. (1992 Yearbook). Reston, VA: NCTM.         [ Links ]

7. Blum, W. & Niss, M. (1991). Applied Mathematical Problem Solving Modelling, Applications, and Links to other Subjects – State, Trends and Issues in Mathematics Instruction. Educational Studies in Mathematics, 22, 37-68.        [ Links ]

8. Brown, L. & Rushowy, K. (2001, Dic. 7). Poor math scores raise alarm. Educational Reporters. Disponible en: http://www.thestar.com/NASApp/cs/ContentServer?pagename=thestar/Layout/Article_Type1&c=Article&cid= 1007681414571&call_page=TS_News&call_pageid=968332188492&call_pagepath=News/News&col=968793972154        [ Links ]

9. Cockroft, W. H. (1985). Las Matemáticas si cuentan. Madrid: Ministerio de Educación y Ciencia.        [ Links ]

10. Delors, J. (1996). La educación encierra un tesoro (Informe a la UNESCo de la comisión internacional sobre la educación para el siglo XXI). Madrid: Santillana.         [ Links ]

11. Dick, T. (1992). Super Calculators: Implications for Calculus curriculum, Instruction and Assessment. En J. Fey y C. Hirsch (Eds.), Calculators in Mathematics Education (1992 Yearbook). Reston, VA: NCTM.         [ Links ]

12. Dunham, P.H. y Dick, T.P. (1994). Research on Graphing Calculators. The Mathematics Teacher, 87(6), 440-445.        [ Links ]

13. Ensor, P. (2001). From Preservice Mathematics Teacher Education to Beginning Teaching: A Study in Recontextualizing. Journal for Research in Mathematics Education, 32(3), 296-320.        [ Links ]

14. Fey, J., Cuoco, A., Kieran, C., McMullin, L. y Zbiek, R.M. (Eds.) (2003). Computer Algebra Systems in Secondary School Mathematics Education. Reston, VA, USA: National Council of Teachers of Mathematics.        [ Links ]

15. Galbraith, P. y Haines, C. (1998). Disentangling the nexus: Attitudes to Mathematics and Technology in a Computer Learning Environment. Educational Studies in Mathematics, 36, 275-290.        [ Links ]

16. Galbraith, P. y Haines, C. (2001). Conceptual and procedural demands embedded in modelling tasks. En J.F. Matos, W. Blum, S.K. Houston and S.P. Carreira (Eds.), Modelling and Mathematics Education. Applications in Science and Technology. Chichester, UK: Horwood Publishing.         [ Links ]

17. Herget, W., Heugl, H., Kutzler, B. y Lehmann, E. (2000). Computer Algebra Systems (CAS). Micromath, Autumn, 9-17.        [ Links ]

18. Hilton, P. (2000). Necesidad de una reforma. En N. Gorgorió, J. Deulofeu & A. Bishop (Eds.), Matemáticas y Educación. Barcelona: ICE-GRAÓ.        [ Links ]

19. Hitt, F. (2000). Construction of Mathematical Concepts and the Use of Simbolic Calculators. En T. Etchells, C. Leinbach y D. Pountney (Eds.), The Proceedings of the 4^th International Derive-TI89/92. Liverpool, UK: John Moores University.        [ Links ]

20. Kaput, J. (1992). Technology and Mathematics Education. En D.A. Grows (Ed.), Handbook of Research on Mathematics Teaching and Learning (pp. 515-556). New York: Macmillan.         [ Links ]

21. Kissane, B., Kemp, M. y Bradley, J. (2000). Evaluación y Calculadoras Gráficas. En P. Gómez y B. Waits (Eds.), Papel de las calculadoras en el salón de clase (pp.103-130). Bogotá: una empresa docente.         [ Links ]

22. Kutzler, B. (2000). The Algebraic Calculator as a Pedagogical Tool for Teaching Mathematics. International Journal of Computer Algebra in Mathematics Education, 7(1), 5-23.        [ Links ]

23. Kutzler, B. (2003). CAS as Pedagogical Tools for Teaching and Learning Mathematics. En J. Fey, A. Cuoco, C. Kieran, L. McMullin y R.M. Zbiek (Eds.), Computer Algebra Systems in Secondary School Mathematics Education. Reston, VA, USA: National Council of Teachers of Mathematics.        [ Links ]

24. Leinhardt, G., Zaslavsky, o. y Stein, M.K.(1990). Functions, Graphs, and Graphing: Tasks, Learning, and Teaching. Review of Educational Research, 60(1), 1-64.        [ Links ]

25. Marcelo, C. (1992). Cómo conocen los profesores la materia que enseñan. Algunas contribuciones de la investigación sobre conocimiento didáctico del contenido. Ponencia presentada al Congreso "Las didácticas específicas en la formación del profesorado", Santiago de Compostela, España, 6-10 de julio.        [ Links ]

26. Mohammad, I. (1999). A Study of the Technology Competencies of Preservice Secondary Mathematics Teachers (Tesis Doctoral, University of Illinois at Urbana-Champaign). Illinois,USA: University Microfilms International.         [ Links ]

27. NCTM (2000). Principles and Standards for School Mathematics. Reston, VA: The National Council of Teachers of Mathematics. Disponible en: http://standars.nctm.org/document/index.htm        [ Links ]

28. Novak, J. y Gowin, D. (1988). Aprendiendo a aprender. Barcelona, España: Martínez Roca.        [ Links ]

29. Ortiz, J. (2000). Modelización y calculadora gráfica en la formación inicial de profesores de matemáticas. Granada: Universidad de Granada.        [ Links ]

30. Ortiz, J. (2002). Modelización y Calculadora Gráfica en la Enseñanza del Álgebra. Estudio Evaluativo de un Programa de Formación. Granada, España: Universidad de Granada.        [ Links ]

31. Ortiz, J. (2004). Representations and Graphic Calculator in Mathematical Teaching. A Study with Calculus Tutors. En J. Böhm (ed.), Proceedings of the Technology and its Integration in Mathematics Education (TIME-2004). Linz (Austria): bk Teachware Series.        [ Links ]

32. ortiz, J., Rico, L. y Castro, E. (2007). organizadores del currículo como plataforma para elconocimiento didáctico. Una experiencia con futuros profesores de matemáticas. Enseñanza de las Ciencias. 25 (1) (En prensa).        [ Links ]

33. Rico, L. (1997). Dimensiones y componentes de la noción de currículo. En L. Rico (Ed), Bases teóricas del currículo de matemáticas en educación secundaria (Cap.7). Madrid: Síntesis.        [ Links ]

34. Ruthven, K. (1992). Personal Technology and Classroom Change: A British Perspective. En J. Fey y C. Hirsch (Eds.). Calculators in Mathematics Education (1992 Yearbook). Reston, VA: NCTM.        [ Links ]

35. Ruthven, K. (2002). Assessment in Mathematics Education. En L. Haggarty (Ed.), Teaching Mathematics in Secondary Schools. Londres, UK: Routledge Falmer/ Open University.        [ Links ]

36. Short, E. (1985). The Concept of Competence: Its Use and Misuse in Education. Journal of Teacher Education, 36(2), 2-6.        [ Links ]

37. Streun, A, Harskamp, E. y Suhre, C. (2000). The Effect of the Graphic Calculator on the Students’ Solution Approaches: A Secondary Analysis. Hiroshima Journal of Mathematics Education, 8, 27-39.        [ Links ]

38. Super, D. (1992). Implementing Calculators in a District Mathematics Program: Three Vignettes. En J. Fey y C. Hirsch (Eds.), Calculators in Mathematics Education (1992 Yearbook). Reston, VA: NCTM.         [ Links ]

39. Trouche, L. (2000). New Technological Environments: New Constraints, New Opportunities for the Teacher. The International Journal of Computer Algebra in Mathematics Education, 7 (3), 165-179.         [ Links ]

40. Trouche, L. (2005). Calculators in Mathematics Education: A rapid evolution of tools, with differential effects. En D. Guin, K. Ruthven y L. Trouche (Eds), The Didactical Challenge of Symbolic Calculators. New York, USA: Springer.        [ Links ]

41. Usiskin, Z. (2000). Educating the Public about School Mathematics. UCSMP Newsletter, 26, Winter, 4-12.        [ Links ]

42. Waits, B. (2000). Computadoras en el salón de clase: una mirada hacia el futuro. En Gómez, P. y Waitts, B.(Edits). Papel de las calculadoras en el salón de clase. pp. 195-202. Bogotá: una empresa docente.        [ Links ]

43. Waits, B. y Demana, F. (1996). A Computer for All Students – Revisited. The Mathematics Teacher, 89(9), 712-714. Disponible en: http: //emptweb.mps.ohio-state.edu/dwme/papers/revisited.pdf        [ Links ]

44. Waits, B. y Demana, F. (1998). The Role of Graphing Calculators in Mathematics Reform. ohio, USA: The ohio State University. Disponible en: http: //emptweb.mps.ohio-state.edu/dwme/papers/roleofgraphcalc.pdf         [ Links ]