Tomografía acústica axial computarizada  para flujos convectivos de gas (aire)

 Carlos González, Rodney Reyna Regnoult

Carlos González

Licenciado en Física, Msc. en Física. Departamento de Física, Facultad de Ingeniería, Universidad Central de Venezuela. Departamento de Física Aplicada. Universidad Central de Venezuela.dejgonzalez@cantv.net .

Rodney Reyna Regnoult

Profesor Especialidad de Física. M.Sc.  Física de los Ensayos no Destructivo. Dpto. Formación General y Ciencias Básicas. Universidad Simón Bolívar. Universidad Simón Bolívar.rodneyrey@hotmail.com

RESUMEN

Como bien es sabido la tomografía axial computarizada tiene múltiples aplicaciones en el ámbito médico,  industrial, y se emplea para la elaboración de los  tomogramas con radiaciones ionizantes, rayos x, entre otras.  En  este trabajo se aplica la tomografía axial computarizada con ultrasonido para la generación de imágenes de flujos convectivos de aire caliente en régimen estacionario utilizando transductores  ultrasónicos para gases de una frecuencia de 40Khz. Para la generación de los  tomogramas se  utiliza el algoritmo de la retroproyección filtrada de radón como la dependencia del sonido al cambio de temperatura en el gas.

Palabras clave: Tomografía acústica, retroproyección filtrada, Gas en régimen estacionario.

ABSTRACT

Computarized axial acoustic tomography for convective gas flow (air)

As it is well known the computarized tomography has many applications in the medical and industrial scope and is used for the preparation of the tomograms with ionizing radiation, x-rays, among others. In this work they apply the ultrasound computarized axial tomography for creating images of the convective flow of hot air at steady state using ultrasonic transducers for gas at a frequency of 40 Khz. For generating tomograms  the filtered backprojection algorithm of radon is used as the dependence of the sound in response to the temperature change in the gas.

Keywords: acoustic tomography, filtered retroproyeción, gas at steady state.

RÉSUMÈ

Tomographie acoustique axiale numérique de flux convenctifs de gaz (aire)

Comme on le sait déjà, la tomographie axiale numérique a des multiples applications dans le domaine médical, industriel et on l’emploie pour l’élaboration des tomogrammes avec des radiations ionisantes des rayons X entre autres. Dans ce travail, on applique la tomographie axiale numérique avec ultrasons pour la génération d’images de flux convectif d’air chaud en régime stationnaire en utilisant des transducteurs ultrasoniques pour gaz d’une fréquence de 40 Khz. Pour la génération des tomogrammes on utilise l’algorithme de la rétroprojection filtrée de radon ainsi que la dépendance du son selon le changement de température du gaz.

Mots clés: Tomographie acoustique, rétroprojection filtrée, gaz en régime permanent.

RESUMO

Tomografía acústica axial computarizada  para fluxos convectivos de gás (ar)

Como bem é sabido a tomografía axial computarizada tem múltiplas aplicações no âmbito médico, industrial, e se empregam para a elaboração dos  tomogramas com radiaciones ionizantes, raios x, entre outras.  Neste  trabalho aplica-se a tomografía axial computarizada com ultrasonido para a geração de imagens de fluxos convectivos de ar quente em regime estacionario utilizando transductores  ultrasónicos para gases de uma frequência de 40Khz. Para a geração dos  tomogramas utiliza-se o algoritmo da retroproyección filtrada de radon como a dependência do som à mudança de temperatura no gás.

Palavras chave: Tomografía acústica, retroproyeção filtrada, Gás em regime estacionario.

Recibido: julio, 2010 , Aceptado: septiembre, 2010

Introducción

La tomografía deriva del griego tomos, que significa corte o sección La tomografía axial computarizada nace como una técnica de diagnóstico en medicina mediante la visualización por rayos x  después de ser descubierta por Roentgen en 1895.

El fundamento de la tomografía es la adquisición de una imagen  de un corte transversal  de un objeto a partir de proyecciones transversales distintos ángulos de rotación con respecto al mismo, cada una de estas imágenes es una proyección y la tomografía es la técnica de reconstrucción de imágenes a partir de las proyecciones de un objeto. La palabra Axial deriva de su uso médico, originado porque las proyecciones que se obtienen rotando el tubo y el detector en torno a un eje con relación a los rayos x.

Aunque el uso mayoritario de la tomografía computarizada se realiza en el campo de la medicina, ésta se extiende hasta el campo de los ensayos no destructivos  para su aplicación industrial. (Franco, 2008). El sistema presentado en este trabajo se encuadra dentro de la aplicación de los Ensayos No Destructivos.  

El primer  tipo de escáner tomográfico se desarrollo en los años 70. La adquisición de los datos se realizaba con único detector y una fuente de rayos X, altamente colimada. De esta forma, tanto la fuente como el detector se trasladaban linealmente, después de cada adquisición individual, para cubrir totalmente el objeto de la inspección, antes de rotarlos conjuntamente para la siguiente proyección (Yong, Seizo, 2005).

Uno de los problemas que presentaban los primeros escáneres era el alto tiempo de adquisición. De aquí se derivó la segunda generación, que esencialmente consistía en el mismo scanner de traslación y rotación pero que incluía varios elementos detectores.

La tercera generación  de tomógrafos, se tiene una matriz de detectores suficientemente larga que el campo de visión incluya todo el objeto en cualquier proyección. De esta forma se elimina la traslación lineal, disminuyendo considerablemente el tiempo de adquisición. Esta geometría es la conocida como fanbeam. Geometría en abanico (Schomberg, 1978).

Dentro de la geometría de 3era generación, aumentando el numero de detectores en la dirección perpendicular al plano de la imagen, se obtiene la imagen cone beam (de haz cónico) en contraste con la anteriormente descrita, de haz en el abanico. Los algoritmos de reconstrucción varían entre ambas.

La cuarta generación se considera poco interesante por razones prácticas y económicas, En esta generación, se tiene el sistema detector estacionario en un círculo (rodeando el objeto), y el tubo de rayos X rota durante la adquisición.

La tomografía acústica ha  sido aplicada a la atmósfera la cual permite reconstruir la temperatura “T” y la velocidad del viento estos campos son importantes en muchas aplicaciones prácticas, tales como la meteorología, la propagación de las ondas a través de un ambiente turbulento etc. (Ostashev, Vecherin, 2008).

Ning, Yong, Seizo, (2005). Usaron también el ultrasonido para aplicaciones tomográficas utilizando los cambios de temperaturas para generar imágenes tridimensionales usando los datos obtenidos por las proyecciones ultrasónicas a diferentes ángulos. La característica principal de la tomografía computarizada se ha empleado en la elaboración de  algoritmos que son empleados para la extrapolación de esquemas de los datos incompletos. La tomografía computarizada ha sido una herramienta poderosa particularmente se ha utilizado como una técnica de ensayos no destructivos, sin embargo es muy diversificado el uso hecho a esta donde se ha aplicado la transformada de Radon para procesar las imágenes obtenidos de los datos para generar una imagen espacial del objeto en estudio (Burget, Wombellt, Belchamber,  Betteridget, Lilleyt, 1986).

Asimismo, entre otros trabajos que se han hecho en la tomografía acústica esta el de la evaluación de riesgo de caída de los árboles en pie (estudios fitosanitarios de alineaciones urbanas). Esta técnica permite la determinación y localización con gran exactitud, de defectos y huecos internos en el árbol (Iñiguez, 2007).

Otras de las aplicaciones de la tomografía acústica en la industria es la vigilancia de temperatura del gas en un horno en la boquilla de salida, es importante para el buen mantenimiento de los parámetros de funcionamiento deservicios públicos dentro de las calderas. Dado que la temperatura del gas se relaciona con la velocidad de la onda acústica, una técnica no invasiva basada en mediciones de tiempo de transito a lo largo de determinados caminos de longitud conocida, puede ser ultimado para desarrollar un modelo analítico capaz de predecir la temperatura en el medio gaseoso de la integración de las ecuaciones resultantes, después de la sustitución de una serie de Fourier para la inversa de la velocidad del sonido, se genera un algoritmo para la obtención de una imagen espacial ultimando la distribución de temperatura en el Gas (Roderick,Greif,2003)

El propósito general de la investigación es la realización de tomografía acústica a celdas convectivas de  un gas (aire caliente) en régimen estacionario. Ésta se vincula a la Física de los Ensayos No Destructivo en la Ciencia de la Ingeniería. El modelo matemático que se utilizará para el procesamiento de las imágenes tomográficas y termográficas está dado por la retroproyección filtrada de Radón; esta es una integral de una función que se aplica sobre un conjunto de rectas en un espacio n-dimensional, las proyecciones se realizarán con el ultrasonido. En consecuencia, la representación gráfica de la Transformada de Radón da un conjunto de pequeños objetos que se puede describir con una función Seno (una colección de senos con diferentes fases y amplitudes), generando una Matriz que representa un espacio en píxeles asociada a las múltiples proyecciones ultrasónicas sobre el Gas en régimen estacionario.

Las fórmulas matemáticas para reconstruir una imagen tridimensional a partir de múltiples imágenes axiales planas fueron desarrolladas por el matemático Johann Radon. La transformada de Radon bidimensional, es una transformación integral que consiste en la integral de una función sobre un conjunto de rectas. Por ejemplo, una línea la representamos por xcosq +ysinq = s, donde s es la mínima distancia desde la recta al origen y  es el ángulo que forma el eje x con el vector posición del punto de la recta más cercano. Al origen, entonces tenemos:

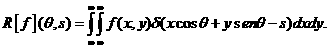   (Ecuación 1)

Siendo R las proyecciones que producen el objeto cuya imagen es f(x,y). A fin de calcular la imagen a partir de las proyecciones es necesario calcular la transformada inversa de Radon. Existen diversos algoritmos inversos de la transformada de Radon computacionalmente eficientes para el caso bidimensional. El problema reside en la imposibilidad de definir el conjunto completo de las integrales de la ecuación anterior. La imagen solo queda determinada por el conjunto infinito de sus proyecciones, pero no por cualquier conjunto finito de proyecciones.

Existe un algoritmo inverso de la transformada de Radon computacionalmente eficiente para el caso bidimensional llamado retroproyección filtrada. El método se basa en el teorema de “cortes de Fourier” o teorema de proyección. Según este teorema, si disponemos de las proyecciones de una imagen es posible determinar cuál es esa imagen calculando una transformada bidimensional inversa de Fourier. El método básicamente consiste en sumar los perfiles de las proyecciones adquiridas (véase la integral inversa Ecuación 2)

                    (Ecuación 2)                          

Procedimiento Experimental

En este trabajo se describe la obtención de tomografías axiales a flujos convectivos de aire estacionario, en régimen laminar, producidos mediante elementos calefactores. Al calentarse el elemento calefactor por conducción al incrementar la temperatura de este produce una convección del aire del tipo natural en régimen laminar el cual asciende de manera vertical. Luego posterior a esto se hacen proyecciones ultrasónicas de un transductor emisor a un receptor. Incrementando la rotación del elemento calefactor hasta 180 grados.  

Mediante la retroproyección filtrada o inversa de la transformada de Radón, se obtiene un corte axial de las celdas convectivas del aire caliente por corrimiento de fase por la variación de las propiedades mecánicas del medio.

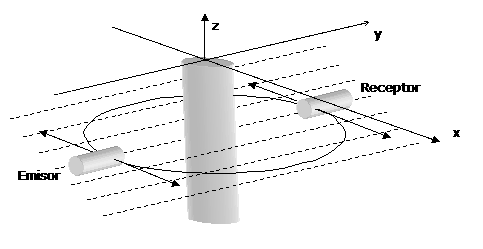
 Figura 1. Representación esquemática del sistema de barrido del emisor y el receptor donde se mueven solidariamente haciendo un barrido a lo largo del eje x, mientras se mide el tiempo que demora un pulso ultrasónico en ir del emisor al receptor a lo largo del eje y, para luego girar alrededor del eje z un ángulo de 6 grados repitiéndose los barridos hasta completar 180º.

 

Fig. 2 Sistema de barrido unidireccional radial con los rieles y los transductores emisor receptor.

 En este trabajo se utilizó el algoritmo de retroproyección filtrada con frecuencia espacial de 3 cm-1 la cual se corresponde con el paso de discretización espacial (0,3 cm).  El paso de rastreo angular empleado es de 6º.

Algoritmo de Retroproyección Filtrada de Radon

Para la inversión de los datos en base a la transformada de Radon, se utilizó el desarrollo teórico mostrado en el texto de A. Ishimaru (1986). Trabajos como el de Burget (1986) muestran aplicaciones prácticas de la tomografía industrial.

En este trabajo se utilizó el algoritmo de retroproyección filtrada con frecuencia espacial de 3 cm-1 la cual se corresponde con el paso de discretización espacial (0,3 cm).  El paso de rastreo angular empleado es de 6º.

 

 Este código correspondiente a la inversión de los datos almacenados como la matriz  p[i,j] de tamaño N×N donde i,j  corresponde  respectivamente a desplazamientos espacial y angular; Di es el diámetro de la región barrida y w la frecuencia de corte (de filtrado).

Resultados obtenidos mediante la Tomografía Acústica Axial Computarizada  para Flujos Convectivos de Gas (Aire)

La figura  3 muestra la tomografía axial  computarizada para el caso de cuatro toberas  de las cuales sale aire caliente, la termografía infrarroja tomada desde la parte superior del eje “y” la fotografía del montaje, en el cual se utilizó humo para poder visualizar el flujo convectivo, claramente en  régimen laminar.  

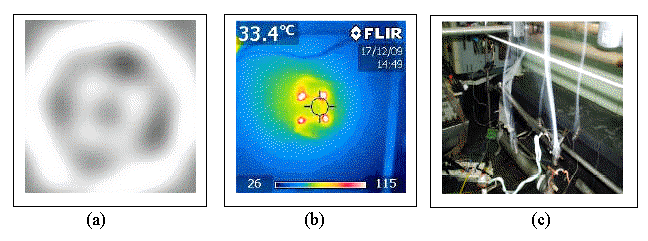
 Figura 3. (a) Tomografía acústica axial computarizada en volt donde el color  más oscuro representa mayor  corrimiento de fase con relación a la distribución del gradiente de temperatura en el humo o flujo de aire que se produce por convección en el elemento calefactor, Con una resolución de 25 x 25 pixeles, (b) termografía infrarroja en grados Celsius del material del  elemento calefactor que se produce por conducción y (c) fotografía del montaje experimental. La tomografía corresponde a un corte a 5 cm de los bordes superiores de las toberas.

 Discusion y Análisis de Resultados

La tomografía acústica representa serias dificultades. Dado que se presenta varios fenómenos físicos como son la reflexión, refracción y difracción del haz ultrasónico en el gas (aire caliente). Pudiéndose presentar información adicional no asociado a los incrementos de temperatura al obtener  las imagen; como también motivado a la turbulencia o la  no laminaridad del gas presentándose un  problema por la geometría,  ya que para la aplicación de la retroproyección filtrada debe de existir simetría en este tipo de ensayo.

A su vez por la forma en que se produjo la laminaridad del gas  en el elemento calefactor fue por convección de tipo natural, corroborando este hecho por inspección visual con trazadores de humo (aceite de motor).

Es importante que al obtener los resultados en la fase experimental lo que se observa en la imagen es un corrimiento de fase que se produce en el sistema de adquisición de datos producto de la variación de las propiedades mecánica del medio cambiando el tiempo de vuelo.

Se obtiene del gradiente temperatura producto de una diferencia de potencial de un elemento resistor (Constatan),  generando una diferencia de fase en el sistema de adquisición de datos.

Se puede relacionar el corrimiento de fase con el gradiente de temperatura. En un desarrollo de primero orden hecho por Gonzáles (2010) nos permite obtener la relación mostrada en la Ec. (3)

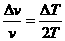      Ecuación (3)

 Donde v es la velocidad del sonido y T la temperatura absoluta. ΔS representa incrementos finitos de la magnitud S.

Por otra parte, la relación entre el corrimiento de fase y el desplazamiento, también hasta primer orden, es de la forma mostrada en la Ec. (2)

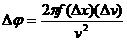         Ecuación (4)  

 Donde φ es el corrimiento de fase, f  la frecuencia y Δx el incremento espacial del sistema de rastreo. Utilizando la ecuación de arriba tenemos que en función de la variación unitaria de la temperatura, el corrimiento de fase (Constantino, Ozanyan, 2008) tiene la forma mostrada en la Ec. (3)

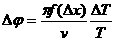         Ecuación (5)

 En el sistema experimental se tienen limitaciones en cuanto a la resolución espacial y a la sensibilidad del detector de fase. Para el sistema utilizado, el gradiente de temperatura detectable resulto ser de 4K/mm

 Conclusiones

Se ha logrado realizar tomografías acústicas partiendo de las proyecciones ultrasónicas que se dan por los cambios de velocidad de estas ondas, producto  del cambio de temperatura en el flujo gas (aire caliente) laminar en régimen estacionario. Adicionalmente, la técnica desarrollada puede aplicarse a investigaciones sobre mecánica de fluidos, ciencias de la educación científica, física aplicada, laboratorio para el aprovechamiento de las técnicas de interfaz del puerto paralelo del computador a bajo costo y para las diferentes áreas asociadas a sistemas de adquisición de datos. También sirve para la determinación de velocidades de desplazamiento de gases.

 Agradecimiento: La realización de este trabajo ha sido posible gracias a la colaboración de la Dirección de Postgrado y a la Dirección de Coordinación Administrativa de la Facultad de Ingeniería de la Universidad Central de Venezuela y al laboratorio de Técnicas Electromagnéticas Aplicadas a los Ensayos no Destructivos de la Escuela de Física Aplicada.

Referencias

1.Akira Ishimaru, (1999). Electromagnetic Wave Propagation, Radiation, and Scattering. USA: Ed. Prentice Hall.        [ Links ]

2.Burget RE., Wombellt RJ. (1986). Radon space techniques for evaluation of industrial tomography systems. (Documento en línea). Disponible: http://www.sciencedirect.com/science . [Consulta: 2009, junio 8].        [ Links ]

3.Constantino EPA, Ozanyan KB. (2008). Sinogram recovery for sparse angle tomography using a sinusoidal Hough transform. (Documento en línea). Disponible: http://iopscience.iop.org/0957-0233/19/9/094015. [Consulta: 2009, Marzo 7].        [ Links ]

4.Franco Lucia. (2008). Desarrollo, puesto en marcha y caracterización de un sistema de   tomografía axial computarizada para Ensayos no Destructivos. (Resumen en línea). Tesis doctoral no publicada Faculta de Física (USC). Universidad de Santiago de Compostela. Disponible: http://books.google.co.ve  . [Consulta: 2009, junio 15].

5.González Carlos, Reyna Rodney. (2010). Modelos Computacionales en ingeniería Desarrollo novedosos y aplicaciones. Memorias del X Congreso Internacional de Métodos numéricos en  Ingeniería. (PS 139). Mérida, Venezuela. Sociedad Venezolana de Métodos Numéricos en Ingeniería.          [ Links ]

6.González Iñiguez. (2007). Clasificación mediante técnicas no destructivas y evaluación de las propiedades mecánicas de las maderas aserrada de coníferas de gran  escuadría para uso estructural. (Documento en línea). Tesis doctoral no publicada, Facultad de Física, Universidad Politécnica de Madrid. Disponible: http://oa.upm.es/415/ [Consulta: 2009, junio 14].         [ Links ]

7.Ning. Z., Yong J., Seizo K., (2005). Ultrasonic computerized tomography (CT) for temperature measurements with limited projection data based on extrapolated filtered back projection (Documento en línea). Disponible: www.sciencedirect.com. [Consulta: 2009, junio 11].        [ Links ]

8.Ostashev Vladimir., Vecherin Sergey. (2008). Recent progress in acoustic tomography of theatmosphere. (Documento en línea). Disponible: http://www.iop.org  [Consulta: 2009, Junio 10].        [ Links ]

9.Roderick, M., Greif, Collier R. (2003). Thermal acoustic tomography. (Documento en línea). Disponible: http://dx.doi.org/10.1121/1.2028714 [Consulta: 2009, junio 14].         [ Links ]

10.Schomberg, H., (1978). An improved approach to reconstructive ultrasound tomography (Documento en línea). Disponible: http://iopscience.iop.org/0022-3727/11/15/004 . [Consulta: 2009, Junio 10].        [ Links ]
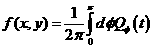
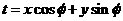