1. Introdução

Nos últimos tempos, com o avanço das Tecnologias Digitais da Informação e Comunicação (TDIC), a disseminação de dados está cada vez mais presente na sociedade, exigindo dos leitores conhecimento e habilidades críticas para a interpretação desses dados e as tomadas de decisões conscientes a partir dessas informações. ^{Ramírez et al. (2021)} enfatizam que, na sociedade dos dados, a Estatística se destaca enquanto ciência necessária para a coleta, o tratamento e a interpretação dos dados. Com eles, a desinformação está cada vez mais presente, sendo acompanhada por dados e representações estatísticas, como os gráficos estatísticos. A desinformação se baseia em uma “informação falsa criada intencionalmente para prejudicar alguém, uma instituição ou país, provocando mal-estar” (^{Carvalho et al., 2021}, p. 186). Dessa maneira, a desinformação tem consequências para a pessoa e a coletividade, sendo necessário, formar cidadãos letrados estatisticamente.

De acordo com ^{Cazorla e Castro (2009)}, quando os dados de uma pesquisa são compartilhados em diversos meios de comunicação, utilizando representações e métodos estatísticos, eles adquirem credibilidade bem como causam e podem gerar uma percepção de veracidade no leitor, mesmo que ele não analise as informações fornecidas para confirmar essa concepção. Isso ocorre porque “os números passam uma ideia de cientificidade, de isenção, de neutralidade” (^{Cazorla & Castro, 2009}, p. 46).

^{Huff (2016)} afirma que a Estatística pode ser utilizada em muitas situações de modo tendencioso, o que pode influenciar uma interpretação equivocada dos dados.^{Delport (2023}) exemplifica essa utilização indevida das representações estatísticas quando mostra gráficos distorcidos para passar uma mensagem de tendenciosidade sobre a Covid-19, enquanto ^{Andrade et al. (2020)} evidenciam gráficos distorcidos divulgados pela mídia. Trabalhos voltados para a dificuldade de interpretação de gráficos são cada vez mais frequentes e mostram a necessidade de pesquisas para essas temáticas. Assim, é perceptível a demanda de um olhar crítico para com esses dados e gráficos, visto que ^{Kahlenberg et al. (2023)} enfatizam como a desinformação influenciou a decisão de muitos cidadãos se vacinarem ou não, em vez dos dados estatísticos.

Nessa perspectiva de necessidade de interpretação de dados divulgados pela mídia, sendo estas desinformações ou não, ^{Kurnia et al. (2023)} evidenciam a necessidade do trabalho do Letramento Estatístico (LE) com estudantes do Ensino Médio, visto que, em seu estudo, esses estudantes apresentaram dificuldades em demonstrar um pensamento crítico diante dos dados. Para ^{Watson e Smith (2022)}, essa criticidade dos dados é essencial para a compreensão da Estatística, que permite o entendimento de fenômenos globais, como a Covid-19.

Dessa forma, há uma preocupação em relação ao discernimento dos cidadãos em habilidades de interpretação coerentes e de tomada de decisões conscientes diante do bombardeio de dados nas mídias. Para ^{Carvalho et al. (2021)}, essas habilidades necessárias aos cidadãos estão atreladas ao LE com relação às dimensões cognitivas e afetivas do indivíduo, que favorecem a compreensão de fenômenos estatísticos a partir das situações do contexto. Isso posto, compreende-se a perspectiva do LE (^{Gal, 2002}) como ferramenta norteadora para o desenvolvimento da criticidade do cidadão diante das informações expostas, principalmente entre os estudantes.

No âmbito educacional, a Estatística tem papel fundamental no desenvolvimento escolar e cidadão dos estudantes. ^{Sutherland et al. (2022)}, ^{Santana (2016)} e ^{Ramírez et al. (2021)} destacam que a Estatística deve ser ensinada nas escolas de forma investigativa, enquanto ^{Ortigoza e Mateus (2021)} enfatizam que conteúdos estatísticos, como as medidas de dispersão, devem ser ensinados na perspectiva de aprendizagem baseada em projetos. Apesar disso, ^{Sutherland et al. (2022)} e ^{Santana (2016)} afirmam que o ensino de Estatística ainda é voltado para cálculos, sem interpretações ou análises críticas.

Assim, este artigo busca explorar as ideias de construção interpretação estatística de estudantes com o boxplot, pois, segundo ^{Lima e Selva (2021)}, estudos que articulam interpretação e construção possibilitam o desenvolvimento de habilidades interpretativas de gráficos. Esta pesquisa tomou como base o LE, a partir de um contexto real dos estudantes, em relação à Covid-19, visto que ^{Andrade et al. (2020)} destacam que o estudo de Estatística deve estar voltado para a utilização de dados reais e que haja um propósito no trabalho com esses dados. Corroborando essas ideias, ^{Bromage et al. (2022)} evidenciam a necessidade de práticas que promovam a aprendizagem significativa de Estatística, rompendo os percalços que os estudantes apresentam ao longo do processo, seja ele no ensino básico ou superior.

O presente estudo tem como objetivo analisar se os aspectos do LE podem contribuir para a compreensão e interpretação do boxplot em um contexto relacionado à Covid-19. Além disso, busca-se identificar se os elementos disposicionais dos estudantes são evidenciados por eles, diante do contexto de redução dos casos da Covid-19 no município de Petrolina, Pernambuco (PE), devido ao avanço da vacinação. Para alcançar tais objetivos, foi desenvolvido um questionário composto por três questões que envolvem a construção e interpretação de um boxplot. Essas questões apresentam dados sobre a diminuição do número de óbitos por Covid-19 no mês de janeiro de 2022 na cidade dos participantes da pesquisa, período em que a vacinação avançava e evitava a morte de muitos cidadãos brasileiros.

A partir do embasamento no LE de ^{Gal (2002)}, as próximas seções apresentam, respectivamente, os aspectos teóricos que fundamentam esta pesquisa, algumas discussões sobre o boxplot, destacando aspectos conceituais e relacionados a sua construção, os procedimentos metodológicos da pesquisa, e, na sequência, os resultados obtidos pelas primeiras impressões dos estudantes e descrições no instrumento de pesquisa. Por fim, expomos as conclusões do trabalho.

2. O modelo teórico do Letramento Estatístico de Iddo Gal

O modelo teórico que fundamenta esta pesquisa envolve habilidades e conhecimentos cognitivos e sociais que auxiliam no desenvolvimento cidadão de um indivíduo ativo na sociedade à qual pertence (^{Gal, 2002}). Para Gal (2002, p. 1, tradução nossa), “o Letramento Estatístico é concebido como a capacidade de interpretar, avaliar criticamente e comunicar informações e mensagens estatísticas”, sendo composto por dois elementos inter-relacionados:

(a) a capacidade das pessoas de interpretar e avaliar criticamente informações estatísticas, argumentos, ou fenômenos estocásticos, que eles podem encontrar em diversos contextos; e, quando relevante, (b) sua capacidade de discutir ou comunicar suas reações a tais informações estatísticas, como sua compreensão do significado da informação, suas opiniões sobre as implicações dessas informações ou suas preocupações em relação à aceitabilidade das conclusões dadas.

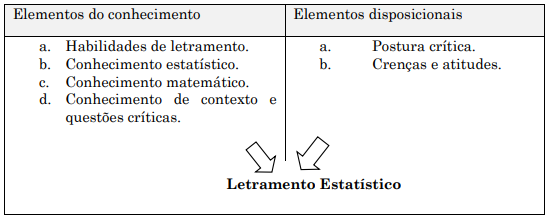
Para ^{Gal (2002)}, os componentes do LE compreendem elementos do conhecimento (habilidades de letramento, conhecimento estatístico, conhecimento matemático, conhecimento do contexto e questões críticas) e elementos de disposição ou disposicionais (postura crítica e crenças e atitudes). O Quadro 2 apresenta esses aspectos.

Quadro 2 Modelo de Letramento Estatístico 

Fonte: Adaptado de^{Gal (2002)}

Apesar de se constituírem elementos fundamentais para o desenvolvimento do LE, vale destacar que ^{Gal (2002)} considera esses componentes como interdependentes. Isso significa que nenhum deles garante por si só o LE, sendo necessário o conjunto de todos os elementos atuando de forma inter-relacionada.

Dessa maneira, enquanto elemento do conhecimento, as habilidades de letramento se referem à capacidade de o indivíduo ler, interpretar e compreender textos ou informações descritas na língua materna para evitar interpretações equivocadas. O conhecimento estatístico se refere à habilidade do indivíduo para interpretar e compreender conceitos estatísticos, utilizados em diferentes áreas do conhecimento para representar ou sumarizar dados de pesquisas. Já o conhecimento matemático, terceiro componente dos elementos cognitivos, relaciona-se às habilidades voltadas para os saberes dos conceitos e operações matemáticas que auxiliam na representação e divulgação dos dados.

^{Cazorla e Castro (2009)} ressaltam a importância dos conhecimentos para o desenvolvimento do pensamento crítico, uma vez que as representações numéricas e estatísticas são amplamente utilizadas por mídias digitais e veículos de informação na divulgação de dados. Devido à natureza racional e aparente veracidade da Matemática, muitos leitores não questionam as informações apresentadas, o que pode levar a problemas relacionados à desinformação.

O quarto elemento da cognição, o conhecimento de contexto e as questões críticas, está diretamente relacionado ao conhecimento dos cidadãos sobre eventos que ocorrem ou ocorreram na sociedade em diversos níveis (local, regional, nacional e internacional). Esse saber é fundamental para compreender os vários elementos que influenciam determinado evento e que podem não ser evidenciados pelos meios de comunicação. Além disso, as questões críticas referem-se à capacidade de questionar de forma crítica as informações apresentadas sobre certa situação. Esse questionamento é embasado no conhecimento de contexto, uma vez que a maioria das variáveis relacionadas a esse evento é considerada com base em um entendimento real do contexto da situação. Em relação aos elementos da disposição, ^{Gal (2002)} destaca que a postura crítica, as crenças e as atitudes são construídas com base nas experiências vividas em sociedade e nas relações interpessoais, tanto no contexto escolar quanto no familiar e social, levando em consideração as características individuais.

3. O boxplot na formação escolar e cidadã dos estudantes

Considerando a facilidade e praticidade no compartilhamento de informações, bem como no acesso a esses dados, a interpretação de gráficos estatísticos emerge como necessidade social, principalmente da sociedade brasileira. Segundo ^{Huff (2016)}, os gráficos estatísticos podem ser empregados para passar uma mensagem tendenciosa aos leitores a partir de manipulações. ^{Delport (2023)} destaca a necessidade do desenvolvimento crítico sobre as interpretações de informações estatísticas, numa perspectiva de questionamento. Assim, uma interpretação coerente e uma análise crítica das informações são necessárias para o desenvolvimento do LE.

Neste estudo, consideramos o gráfico boxplot e discorremos sobre aspectos conceituais relacionados a sua construção e interpretação. O boxplot foi evidenciado pela primeira vez pelo estatístico estadunidense ^{Tukey (1977)}, na Análise Exploratória de Dados (EDA). Segundo ^{Carvalho et al. (2019)}, a EDA é uma abordagem inicial com os dados de uma pesquisa que tem como objetivo principal descrevê-los de forma gráfica e numérica para, assim, identificar regularidades e tendências nos dados.

Também conhecido como diagrama de caixas ou box and whisker plot, o boxplot consiste em uma representação gráfica estatística amplamente utilizada para sumarizar dados quantitativos. Ele engloba várias medidas estatísticas, como medidas de tendência central e de posição. Esse diagrama pode ser utilizado para diversas finalidades, como visualizar a dispersão dos dados, realizar a abordagem inicial dos dados, conforme proposto na EDA, identificar valores extremos ou discrepantes e comparar grupos de amostras de dados por meio de duas ou mais caixas (^{Valladares Neto et al., 2017}).

De acordo com ^{Valladares Neto et al. (2017)}, o boxplot é um gráfico que exibe em sua representação diferentes medidas estatísticas que favorecem a interpretação de dados quantitativos, principalmente referentes à distribuição e ao reconhecimento de valores discrepantes. Para esses autores, em um boxplot, estão presentes medidas de tendência central (a mediana) e de dispersão (os quartis) bem como valores atípicos (outliers) e extremos. ^{Madrid et al. (2022)}) reforçam a necessidade do desenvolvimento de habilidades de leitura de gráficos em um nível de complexidade maior, principalmente o boxplot, importante instrumento de transnumeração. ^{Pandey et al. (2015)}, por exemplo, reforçam essa necessidade quando utilizam o boxplot para a análise de Big Data na Educação. Em conformidade, ^{Ferreira et al. (2016)} mostram as potencialidades do boxplot na análise de elementos químicos, auxiliando a compreender as características deles.

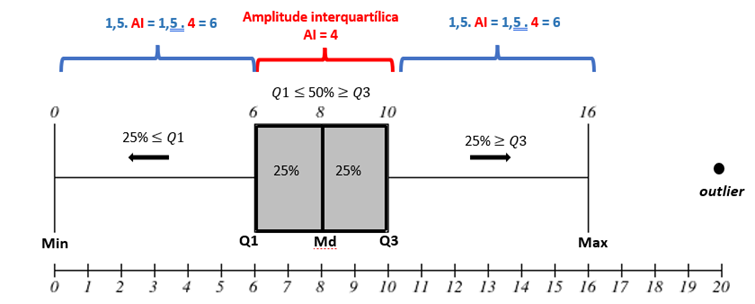
O boxplot apresentado na Figura 1 é um exemplo formado pelas seguintes medidas estatísticas: os valores mínimo e máximo, o primeiro quartil (Q1), a mediana (Md) e o terceiro quartil (Q3). Além disso, temos os valores discrepantes da maioria dos dados, os outliers, definidos em pontos distantes da caixa 1,5 vezes da amplitude interquartílica (AI = Q3 - Q1), identificados por bolinhas (º) e localizados após ou antes das hastes (também chamados de bigodes).

Figura 1 Componentes do boxplot. Fonte: Autores (2023) 

Adotando essa estrutura, na parte da caixa do gráfico que se apresenta preenchida com a cor cinza na Figura 1, ficam localizados 50% dos dados obtidos na pesquisa, 25% entre o Q1 e a mediana e 25% entre a mediana e o Q3, mesmo que as metades da caixa possuam tamanhos diferentes. Quando isso ocorre, percebemos a distribuição dos dados, ou seja, se uma parte da caixa é maior do que outra, indicando que os dados estão mais distribuídos nessa parte; e, quando ocorre o inverso, isto é, uma parte da caixa é menor, os dados estão mais concentrados naquela região. Enquanto isso, à esquerda do Q1, ficam localizados 25% dos dados, e à direita do Q3, outros 25% dos dados, independentemente do tamanho dos bigodes, pois o que ocorre com a distribuição dos dados na caixa do boxplot ocorre nos bigodes. O comprimento da caixa é definido pela diferença entre o primeiro e o terceiro quartil, chamado de Amplitude Interquartílica (AI = Q3 - Q1).

Para definir os valores máximos e mínimos dos bigodes do boxplot e verificar se os dados possuem outliers, é necessário tomar como ponto de partida a amplitude interquartílica. Assim, considerando 1,5 vezes esse intervalo, os valores mínimo e máximo são definidos pela distância da caixa 1,5 vezes à direita para o valor máximo e 1,5 vezes à esquerda para o mínimo. Os dados menores que o valor mínimo e os maiores que o máximo são considerados outliers.

Segundo ^{Edwards et al. (2017)}, a interpretação do boxplot não é tão simples, e a comparação do próprio diagrama com outras representações estatísticas pode ser um obstáculo para a aprendizagem do estudante, principalmente no que se refere à análise das informações em relação ao agrupamento e exibição dos dados, visto que, enquanto outros gráficos são organizados intuitivamente pela frequência dos dados, o boxplot não. ^{Gilchrist e Summers (2007)} utilizaram o boxplot para a produção de um objeto reutilizável com estudantes da Saúde e perceberam as dificuldades encontradas por eles na interpretação.

Isso significa, por exemplo, que, em outros gráficos estatísticos, como o de barras, uma grande frequência dos dados se comporta de forma proporcional ao tamanho dos elementos do gráfico. No entanto, no boxplot, uma grande frequência de um dado reduz o formato das partes do diagrama, já que os dados estão mais agrupados. Esse tipo de comparação, com base em ^{Edwards et al. (2017)}, pode confundir o estudante.

Essas ideias de ^{Edwards et al. (2017)} em relação à comparação com outros gráficos se relacionam com alguns equívocos de estudantes evidenciados nos estudos de ^{Lem et al. (2013)} e ^{Madrid et al. (2022)}, no que se refere ao tamanho dos elementos do boxplot, como bigodes e caixa. Com base nesses autores, os estudantes concluem que a área maior da parte da caixa representa mais dados em comparação com uma área menor da caixa.

As reflexões que emergiram a partir da revisão da literatura, enfatizam a importância e a necessidade do trabalho de construção e interpretação do boxplot com estudantes sob a perspectiva do Letramento Estatístico. Esse gráfico consiste em representação estatística poderosa que permite aos estudantes analisarem e interpretarem um conjunto de dados de maneira eficiente, possibilitando a identificação de tendências e padrões na distribuição. Por oferecer uma visão geral da distribuição dos dados, incluindo conceitos estatísticos importantes (mediana, quartis, valores mínimos e máximos e identificação de outliers), o boxplot possibilita uma compreensão ampla do conjunto de dados, ajudando estudantes a tomarem decisões importantes com base nas informações apresentadas.

Além desses aspectos, a compreensão do gráfico boxplot pode se constituir em um alicerce fundamental para estudos estatísticos mais avançados. À medida que os estudantes progridem para níveis superiores de educação, o conhecimento e a habilidade de interpretar boxplot se tornam cada vez mais relevantes. Ao introduzir esse tipo de gráfico no Ensino Médio, portanto, os estudantes estarão mais preparados para cursos universitários e profissionais que envolvem análise de dados e estatísticas.

4. Percurso Metodológico

O estudo é um recorte de uma pesquisa de monografia de conclusão de curso de Licenciatura em Matemática da Universidade de Pernambuco (UPE), localizada no interior do estado de Pernambuco, Brasil. Os dados foram produzidos com 14 estudantes pertencentes a uma turma do primeiro ano do Ensino Médio de uma escola da rede estadual de ensino do sertão de Pernambuco. Assim, foi realizada uma intervenção com os estudantes para apresentar o boxplot, os elementos que o compõe, a construção e interpretação dele.

Após a intervenção, detalhada também na próxima seção, os estudantes colocaram em prática os conhecimentos acerca do boxplot e elaboraram um diagrama de caixas que representavam as quantidades de mortes por Covid-19 no município de Petrolina no mês de janeiro de 2022. Este período representou o avanço da vacinação em que muitos adultos, principalmente, já tinham tomado pelo menos a segunda dose da vacina e alguns jovens a primeira. O contexto da Covid-19 foi escolhido para desenvolver esta pesquisa, pois, de acordo com ^{Gal (2022)}, durante o ensino de Estatística, o contexto deve ser a base das atividades desenvolvidas.

Para a construção do boxplot, os dados quantitativos utilizados foram coletados diretamente no site oficial da Prefeitura do Município, que registrava as ocorrências diárias da Covid-19 pelos pesquisadores. Eles foram disponibilizados para os estudantes em uma tabela, devido à falta de tempo para a realização da coleta pelos próprios participantes.

O instrumento de produção de dados utilizado neste estudo foi um questionário composto por três questões de interpretação e construção do boxplot, que instigaram os elementos do Letramento Estatístico (LE) de ^{Gal (2002)}, como o conhecimento estatístico, o conhecimento matemático, o conhecimento de contexto e os elementos da disposição. Para isso, foram definidos objetivos de análise para cada item do questionário (Quadro 1).

A questão A explorava os conhecimentos dos estudantes sobre a construção do diagrama. Para isso, eles precisavam identificar as medidas estatísticas necessárias para essa elaboração e expor conhecimentos matemáticos e estatísticos do LE. A questão B requeria do estudante a interpretação gráfica do boxplot e conhecimentos matemáticos e estatísticos. Já a questão C abordava conhecimento de contexto e exposição de elementos da disposição.

As considerações obtidas serão evidenciadas neste artigo preservando o anonimato dos participantes desta pesquisa. Para isso, serão utilizados nomes fictícios para identificá-los. Os dados foram organizados a partir das perguntas do questionário e agrupados em três categorias: primeiras impressões, experiência de construção e interpretação do boxplot.

5. As primeiras impressões dos estudantes sobre o boxplot

Os 14 estudantes participantes, 9 do gênero masculino e 5 do feminino, não conheciam o boxplot e afirmaram que não tinham tido contato algum com o diagrama, seja na escola em anos escolares anteriores ou em outras situações cotidianas, como artigos e notícias. Então, no primeiro contato com o diagrama, os estudantes expressaram espontaneamente as primeiras impressões acerca desse gráfico, após a exposição de um exemplo de um boxplot simétrico proporcionado pelos pesquisadores na lousa da turma.

Um boxplot é considerado simétrico quando as medidas de cada um dos bigodes e das duas metades da caixa são iguais. Isso significa dizer que a distribuição dos dados é normal. No entanto, quando essa distribuição dos dados não é normal, as partes do boxplot, os bigodes e as duas metades das caixas, aparecem de forma assimétrica. Assim, se a dispersão dos dados for maior entre o primeiro quartil e a mediana, por exemplo, a primeira metade da caixa será maior que as demais partes. A aluna Rebeca evidenciou que o boxplot era semelhante a “um campo de futebol”; associando o diagrama ao formato retangular que caracteriza o boxplot na região da caixa. No entanto, vale destacar que, após a exposição de outros diagramas, esses, por sua vez, assimétricos, essas percepções da estudante mudaram, visto que a caixa não era simétrica.

O boxplot foi apresentado, bem como sua utilização em algumas pesquisas, que mostravam um comparativo entre o preço de diferentes produtos da mesma categoria. Exemplos como esse foram evidenciados para destacar a relevância do gráfico na sociedade. Essa comparação foi importante para a percepção dos estudantes sobre as diferentes tendências do diagrama, com base nos dados fornecidos, podendo ser reduzidos, mais amplos, simétricos ou assimétricos.

Durante esse estudo do boxplot ideias de simetria foram exploradas, com foco na distribuição de dados coletados e na proporção inversa do tamanho da caixa e dos bigodes do boxplot em relação à quantidade de dados. Os estudantes se mantiveram surpresos, pois a caixa não era simétrica, no entanto, existia a mesma quantidade de dados em cada uma das metades da caixa. Para os estudantes, o fato de uma das metades da caixa possuir tamanho menor que a outra significava que ela possuía uma menor quantidade de dados do que a maior, corroborando com os estudos de ^{Edwards et al. (2017)}.

O estudo sobre o gráfico boxplot e seus elementos como caixa, bigodes, distribuição dos dados e medidas presentes no diagrama foi fundamental para orientar as atividades subsequentes, especialmente considerando que os estudantes não haviam tido contato prévio com esse tipo de diagrama. No entanto, é importante ressaltar que apenas um estudo não é suficiente para uma aprendizagem completa desse gráfico. É necessário proporcionar aos estudantes oportunidades contínuas de prática e aprofundamento a fim de consolidar seu entendimento e habilidade na interpretação do boxplot.

6. A experiência de construção e interpretação do boxplot com os estudantes

Na construção do boxplot com base nos dados referentes às mortes por Covid-19 em janeiro de 2022 (Figura 2), constatamos que 5 estudantes não realizaram tentativas de elaboração. Em contrapartida, 3 estudantes conseguiram determinar corretamente as medidas estatísticas, como a mediana (Md), o primeiro e terceiro quartis (Q1 e Q3), além dos valores máximos e mínimos. No entanto, esses estudantes precisavam analisar e restringir os valores máximos e mínimos ao conjunto de dados, uma vez que o valor máximo fornecido era 2,5 e o mínimo era -1,5.

Figura 2: Boxplot de mortes por COVID-19 em Janeiro de 2022. Fonte: Autores (2023) 

Considerando que o menor e o maior valor dos dados correspondiam a zero e duas mortes, respectivamente, esses valores numéricos deveriam ser adotados como mínimo e máximo no boxplot. Surpreendentemente, o estudante Márcio, assim como outros dois estudantes, restringiu apenas o valor mínimo, resultando em um diagrama incorreto para a extremidade direita do terceiro quartil, que representa o valor máximo (Figura 3). Apesar desse equívoco, os estudantes demonstraram conhecimento sobre as etapas envolvidas na construção de um boxplot, especialmente na identificação das medidas necessárias.

Figura 3: Construção do boxplot pelo estudante Márcio. Fonte: Autores (2023) 

De maneira semelhante, outros estudantes enfrentaram dificuldades ao restringir os valores encontrados em relação ao conjunto de dados e esboçaram o diagrama com o valor mínimo de -1,5 e o máximo de 2,5. Isso revela que esses estudantes não realizaram uma reflexão adequada sobre o diagrama construído em relação à quantidade de mortes possíveis, uma vez que essa variável quantitativa é discreta e não pode ser representada por valores numéricos negativos ou decimais. A habilidade de reflexão e visão crítica sobre os dados é fundamental para o desenvolvimento do LE, conforme defendido por ^{Gal (2002)}.

É possível que esses estudantes tenham desconsiderado a possibilidade de incoerência desses valores e não tenham realizado uma reflexão aprofundada sobre o assunto. ^{Cazorla e Castro (2009)} afirmam que a utilização de métodos estatísticos e matemáticos na análise de dados transmite ao leitor uma ideia de veracidade e racionalidade, mesmo sem uma análise crítica por parte do leitor. Assim, a falta de uma reflexão crítica pode ter influenciado a impressão limitada dos estudantes em relação à representação dos dados no boxplot.

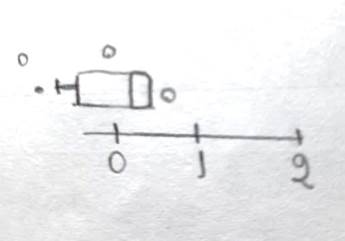
As ideias de ^{Cazorla e Castro (2009)} também podem ser aplicadas aos registros dos estudantes João e Pedro, que enfrentaram dificuldades na identificação do terceiro quartil (Q3) e da amplitude interquartílica (AI), respectivamente. Além disso, esses educandos não demonstraram reflexões críticas sobre suas construções, o que comprometeu a elaboração correta dos diagramas para uma representação contraditória dos dados apresentados na tabela. Um exemplo disso é o boxplot criado por João, no qual todas as medidas tinham valor numérico igual a zero (Md = Q1 = Q3 = Máx = Min = AI = 0). Apesar disso, o diagrama exibiu uma estrutura não nula relacionada a outras medidas na reta numérica (Figura 4).

Figura 4: Construção do boxplot pelo estudante João 

Embora alguns estudantes tenham enfrentado dificuldades ao construir o boxplot, seja devido a operações com inteiros ou à identificação incorreta de algumas medidas estatísticas a partir dos dados, é importante ressaltar que eles demonstraram compreender a elaboração de um diagrama e a determinação de medidas-chave, como medianas, primeiro e terceiro quartis, amplitude interquartílica, valores máximo e mínimo e outliers. Essas dificuldades pontuais não invalidam o entendimento geral deles sobre a criação de um boxplot e sua capacidade de interpretar e analisar um conjunto de dados estatísticos.

Na segunda questão (Questão B), os estudantes foram desafiados a interpretar o gráfico referente ao número de mortes em janeiro de 2022 e justificar por que o digrama possuía apenas um bigode. Era esperado que os 14 estudantes que concluíram o questionário reconhecessem que, nesse caso, o valor mínimo, o primeiro quartil e a mediana possuíam o mesmo valor, ou seja, Min = Q1 = Md = 0. Isso ocorreu, pois, com o avanço da vacinação, a quantidade de mortes por Covid-19 foi baixa em janeiro de 2022 e, na maioria dos dias desse mês, foi igual a 0 no município estudado.

Dois estudantes argumentaram que a existência de apenas um bigode no boxplot de janeiro de 2022 ocorreu “porque o mínimo foi negativo”. Embora esses estudantes tenham fornecido uma informação correta em relação ao valor mínimo, considerando que Q1 = 0 e AI = 1 (AI= Q3 - Q1), o valor mínimo inicialmente encontrado foi um número negativo: Min = Q1 - 1,5. AI = 0 - 1,5. 1 = - 1,5. O valor do conjunto de dados era 0, e o valor mínimo não pode ser menor que o menor dado. Portanto, apenas essa justificativa não fornece fundamentos suficientes para compreender a existência de apenas um bigode.

Por outro lado, 3 estudantes apresentaram a mesma concepção já discutida anteriormente sobre a relação entre a quantidade de dados e a aparência do boxplot. Para eles, o gráfico possuía apenas 1 bigode “porque a quantidade de dados é menor”. Essas ideias corroboram os resultados de ^{Lem et al. (2013)} acerca das concepções dos estudantes sobre as características visuais do boxplot. Mas, como essa afirmação dos estudantes é sucinta, ela pode ser questionada sobre a quantidade à qual eles referiram, se é a quantidade total de dados (31 dados, pois janeiro possui 31 dias) ou a de dados à esquerda da mediana.

Nossas análises sugeriram algumas conclusões acerca do posicionamento desses estudantes. Em relação ao quantitativo total de dados, visto que janeiro possuía mais dados que abril, é possível concluir que a quantidade de dados naquele mês não era menor. No entanto, como aproximadamente 65% dos dados de janeiro eram iguais a 0, é possível que os estudantes tenham intuído que a quantidade de dados era menor pelo fato de o 0 representar, em algumas situações, nenhuma quantidade. Assim, as quantidades 1 e 2 apareceram menos, o que pode ter influenciado para essa percepção errônea de que havia menos dados.

Outro fator que pode ter influenciado as respostas desses estudantes diz respeito à ausência de um dos bigodes do boxplot. A falta desse elemento pode ter ocasionado uma percepção de haver menos dados, já que os elementos do diagrama estavam reduzidos, ou seja, só havia um bigode, e a caixa não apresentava duas metades como outros exemplos trabalhados. De toda a forma, essa justificativa de haver menos dados não esclarece corretamente a razão pela qual o boxplot de janeiro possuiu somente um bigode e metade da caixa. Essas ideias podem ser associadas novamente às concepções de ^{Lem et al. (2013)} e ^{Madrid et al. (2022)} em relação aos bigodes do boxplot e à quantidade de dados.

O estudante Felipe destacou que o boxplot possuía um bigode “porque esse único bigode ocupa a maioria dos números”. Compreendemos que esse aluno quis se referir à parte do diagrama que compreende o valor mínimo, o primeiro quartil e a mediana, ou seja, apenas o segmento inicial da caixa. No entanto, considerando o conjunto de dados de janeiro de 2022, é perceptível que, até a mediana (no valor 0), há 50% dos dados, exatamente a metade. Isso significa que a análise do estudante não garante uma justificativa adequada.

Os demais estudantes apresentaram justificativas que se complementam e formam uma interpretação coerente dos dados, fundamentada em conhecimentos estatísticos, matemáticos e contextuais (^{Gal, 2002}). O estudante Márcio, por exemplo, sugeriu a existência de somente um bigode “porque meu número mínimo de dados é 0/ zero”. Essa afirmação não é suficiente para garantir a existência de apenas um bigode em um boxplot; neste caso, poderia ser incluído nessa justificativa que o primeiro quartil também era zero, para assim a informação ficar completa, como fez o estudante Ricardo.

Para Ricardo, só havia um bigode “porque o mínimo tem o mesmo número do 1ºq”. Assim, ele afirmou corretamente que o valor mínimo era igual ao primeiro quartil e que isso implicava a característica de um dos bigodes do boxplot. O estudante demonstrou os conhecimentos estatísticos e matemáticos suficientes para a solução dessa questão. Em conformidade com essa ideia, o estudante João deixou indicadores de seus conhecimentos de contexto e elementos disposicionais (^{Gal, 2002}) sobre a Covid-19 para evidenciar que havia apenas um bigode “porque tinha diminuído o número de mortes”.

João se baseou na análise do contexto não apresentando explicitamente informações estatísticas e matemáticas, como as levantadas por Márcio. Sua justificativa se ancora nos fatores epidemiológicos que influenciaram diretamente na aparência do boxplot, pois, em janeiro de 2022, houve uma diminuição das mortes pelo vírus. As considerações desses estudantes complementam-se e formam um pensamento embasado no LE de ^{Gal (2002)}.

Quanto ao questionamento da existência de um bigode, foi possível reforçar a percepção de que alguns estudantes relacionaram os conhecimentos de outros gráficos com o boxplot, dificultando a compreensão do diagrama que apresenta características diferentes dos demais gráficos, como já mencionado. Grande parte dos estudantes conseguiu estabelecer relações com conhecimentos estatísticos e matemáticos, enquanto apenas poucos tomaram o conhecimento de contexto para interpretar o boxplot.

Por fim, a última questão (Questão C) envolvia a exposição das crenças dos estudantes em relação à pandemia da Covid-19. Para isso, foi perguntado se algum dos gráficos apresentava um bom resultado para a sociedade e por quê. Esperávamos que os estudantes identificassem o bom resultado no gráfico de janeiro de 2022, já que ele apresentou diminuição no número de mortes. Em resposta a essa pergunta, os estudantes expuseram explicitamente as crenças e a postura deles diante dos resultados de mortes, sendo essas caracterizadas como elementos disposicionais de ^{Gal (2002)}. Por exemplo, o estudante Ricardo afirma que “sim, o segundo gráfico mostra que as mortes estão baixas e que a quarentena está chegando ao fim”. A estudante Fernanda, por sua vez, destacou que o mês que apresentou um bom resultado foi “o de janeiro, pois diminuiu as mortes”. Outros quatro estudantes exibiram respostas semelhantes à dessa aluna. João destacou que “o gráfico de janeiro porque mostra que as coisas parecem estar melhorando”.

Essas percepções mostram que, apesar das crenças dos estudantes estarem voltadas para uma visão coerente com a realidade de que o número de mortes reduzia ao longo do tempo, foi possível perceber ainda a falta de criticidade em relação à análise desses dados referentes ao avanço da vacinação. Essa falta de criticidade por parte dos estudantes do Ensino Médio no que se refere aos dados é também evidenciada por ^{Kurnia et al. (2023)}. A maior parte dos estudantes não apresentou justificativa para a melhoria da situação pandêmica vivida, ou seja, demonstrou mais neutralidade no posicionamento, sem pontuar aspectos políticos e científicos que contribuíram e contribuem para uma diminuição das mortes. Essa neutralidade no posicionamento corrobora os resultados de ^{Kahlenberg et al. (2023)}. Essas posturas do alunado fomentam reflexões em nós sobre uma possível falta de debates sobre as questões sociais nas aulas de Matemática, uma vez que os estudantes não demostraram estar confortáveis para isso nos registros da atividade.

7. Considerações finais

Nossas análises das considerações dos estudantes, indicaram que, em geral, apesar de eles demonstrarem facilidade na construção do boxplot solicitado na atividade, alguns deles apresentaram dificuldades, principalmente em relação à reflexão sobre o processo que realizavam na determinação de máximos e mínimos exibidos no bigode do diagrama. As questões que exigiam do estudante interpretação do boxplot, em relação à exposição das crenças e postura crítica acerca dos fatores qualitativos que influenciavam os dados quantitativos, obtiveram o menor percentual de respostas. Esse resultado mostra que é possível que, no ensino de Matemática, não haja a exploração dessa criticidade; assim, os estudantes não desenvolvem posicionamento diante dos problemas estatísticos e/ou matemáticos.

Além disso, foi possível notar que, embora os estudantes tenham cometido alguns erros no reconhecimento das medidas estatísticas do boxplot, eles demonstraram conhecimento sobre como determinar a mediana, o primeiro e o terceiro quartil e os valores máximos e mínimos de um conjunto de dados quantitativos. No entanto, como os estudantes confundiram a distribuição dos dados no boxplot, é possível que eles não tenham compreendido completamente os significados da divisão dos dados em quartis, visto que, entre cada quartil, existe a mesma quantidade de dados, e eles não demostraram esse entendimento. Para atividades futuras, é possível que os próprios estudantes coletem os dados e, a partir disso, realizem outras atividades de análise dos resultados.

As análises também indicaram que os estudantes, mesmo apresentando traços dos elementos disposicionais, não expuseram opiniões mais amplas que justificassem, por exemplo, a diminuição de mortes por Covid-19 em razão do avanço da vacinação. Isso porque as ações evidenciadas por eles - como o uso de máscaras, álcool 70% e distanciamento social - eram preventivas e não combatentes diretas do vírus. Vale salientar ainda que a vacina é fruto de pesquisas que se fundamentam no conhecimento científico, baseado em estudo e análises de cientistas e outros profissionais capacitados na área, que ocorrem nas universidades, espaço de produção e compartilhamento de conhecimentos.

Podemos concluir que um maior tempo para o desenvolvimento da pesquisa poderia ter auxiliado os estudantes na compreensão e interpretação do boxplot, visto que somente um estudo com caráter de intervenção não garante suficientemente que as aprendizagens tenham sido significativas. Dessa forma, enfatizamos que para abordar todas as potencialidades do boxplot de forma ampla e em diferentes contextos, necessitaríamos de um estudo com maior duração.

Em relação às contribuições da pesquisa do boxplot à interpretação da realidade dos estudantes, observamos que o estudo do diagrama com a variável discreta de mortes por Covid-19 no mês de janeiro de 2022 auxiliou os estudantes a refletirem sobre a realidade social em relação à saúde pública nesse período. Apesar disso, muitos estudantes, como visto nos resultados anteriormente, não expuseram suas opiniões e percepções da realidade. Essa falta de exposição pode ser causada pela ausência de discussões sobre temáticas sociais em sala de aula de Matemática ou de posicionamento crítico e debates.

Assim, com o desenvolvimento do estudo, foi possível perceber a necessidade de pesquisas que visem ao trabalho com boxplot, sob uma perspectiva de estímulo aos elementos disposicionais do estudante. Assim, é possível fomentar o posicionamento crítico, reflexivo e ativo do estudante na sociedade à qual ele pertence, principalmente para que as decisões tomadas por ele sejam conscientes e coerentes com as necessidades da comunidade.