INTRODUCCIÓN

La resolución de problemas matemáticos es un proceso de pensamiento lógico mediante el cual una persona es capaz de encontrar la solución a una situación compleja no planteada previamente a partir del uso de conocimientos matemáticos. Según las Tendencias en Matemáticas y Ciencia de PISA 2003 elaboradas en base a una evaluación minuciosa realizada a 29 países, entre cuyas competencias incluyen "la capacidad de detectar las variables importantes en una situación y de escoger y aplicar uno o varios principios, teoremas o algoritmos matemáticos, relevantes y convenientes para encontrar una solución - y de interpretar y verificar la coherencia de esta solución".

El área de matemática, fundamentada en la resolución de problemas; busca en cada individuo desarrollar habilidades de comprensión, análisis, toma de decisiones y de argumentación (^{Meza Bermeo, 2021}); con el fin de lograr la formación de sujetos altamente competentes que puedan desenvolverse en una sociedad llena de exigencias. De allí la necesidad para los estudiantes de adquirir hábitos de cuestionamiento, como herramienta para resolver problemas (^{Poveda Fernandez, 2020}).

Cada estudiante es poseedor de capacidades, las cuales se han adquirido según el grado de experiencias enriquecedoras adoptadas del contexto inmediato. Pues bien, resolver un problema matemático, resulta para algunos estudiantes una actividad sencilla, sin embargo; para otros resulta difícil o imposible (^{Donoso Osorio et al., 2020}), ello dependerá del nivel de interacción de los docentes para propiciar el desarrollo de competencias. En ese sentido ^{Piñero Charlo et al., (2024)} señala que la capacidad que poseen los docentes para enseñar la resolución de problemas altamente complejos, no resulta suficiente garantía de un adecuado proceso de solucion; pues existen competencias específicas por parte de los alumnos para resolver problemas.

Al respecto existen varios hallazgos bibliográficos, que señalan los diversos puntos de vista acerca de la resolución de problemas. A lo dicho por ^{Molina-Toro et al. (2019)}, este proceso involucra interpretar y comprender; mientras que el contenido es básicamente el conocimiento. Por lo tanto es preciso señalar que esto está referido a cómo los estudiantes piensan y cómo ponen en juego todas sus capacidades para resolver un problema.

Para resolver un problema matemático, siguiendo la línea de varias investigaciones, es necesario poner en juego las fases que este tiene, entendiendo que es un proceso sistemático. Los autores ^{Quiñones Vásquez, y Huiman Tarrillo (2022)}; ^{Llerena-Vivanco (2022)}, y ^{Gualdrón et al., (2020)} sostienen acerca del método Pólya que este se fundamenta en estrategias heurísticas, revelando oportunidades didácticas y formativas para trabajar con los estudiantes; lo que permite la comprensión, acción de hipotetizar, comprobar y plantear nuevas problemáticas. Además, ^{Naranjo Barahona y Caro Roldan (2023)} señalan que, para la resolución de problemas, se debe considerar tres criterios: el primero es que el estudiante deba aceptar que está implicado en el problema; el segundo, es que el problema, debe tener cierto grado de obstrucción o complejidad, y el tercero debe haber una exploración de manera activa del problema en busca de una solución.

Por lo antes expuesto, esta investigación se centra en el estudio de las estrategias de resolución de problemas matemáticos en estudiantes, con el objetivo principal de determinarlas de manera precisa y exhaustiva.

METODOLOGÍA

El presente estudio se basó en un enfoque cualitativo para llevar a cabo la investigación. Dentro de este enfoque, se reconoce que la revisión bibliográfica desempeña un papel fundamental en la identificación de las últimas tendencias y en la síntesis de los fundamentos necesarios para consolidar una disciplina (^{Tramullas, 2020}). Por lo tanto, se optó por utilizar la revisión sistemática de la literatura como método de investigación, siguiendo el enfoque propuesto por ^{Ferreras Fernández (2016)}.

Al adoptar la revisión sistemática de la literatura como método de investigación, se busca garantizar un enfoque sistemático y transparente en la recopilación y análisis de la información relevante. Esto contribuye a la objetividad y la replicabilidad del estudio, al tiempo que proporciona una base sólida de conocimientos existentes para respaldar los hallazgos y las conclusiones del estudio.

Para realizar la revisión sistémica, se ha adoptado cuatro fases, las cuales responde a: búsqueda, evaluación, análisis y síntesis (^{Codina, 2018}).

1. Fase de Búsqueda:

2. Fase de Evaluación:

3. Fase de Análisis:

4. Fase de Síntesis:

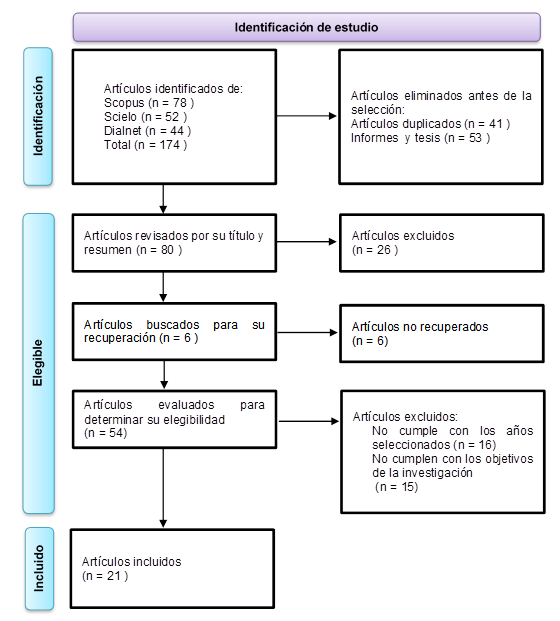
En la elaboración de este artículo, se llevó a cabo un exhaustivo análisis de alrededor de 174 artículos. Se seleccionó una muestra de 21 artículos que cumplen con los criterios de selección establecidos, los cuales se consideraron pertinentes para el objetivo de nuestra investigación. Es importante destacar que se excluyeron aquellos artículos que no provenían de bases de datos confiables, garantizando así la calidad y la validez de la información utilizada en este estudio.

Figura 1 Diagrama del método PRISMA 

RESULTADOS Y DISCUSION

Existen varias teorías fundamentales que desempeñan un papel crucial en la resolución de problemas matemáticos. A continuación, se presentan algunas de estas teorías:

Desde el punto de vista teórico la resolución de problemas sitúa al alumno en un plano activo del proceso de enseñanza y aprendizaje. Establece un tipo de actividad mental y una modalidad compleja de conducta. Posibilita abordar desde diversos niveles de trabajo, diversos niveles de contenido matemático y tiene distintas formas de ser explícito del modelo mental que conduce a la obtención de soluciones (^{Torres et al., 2022}).

A nivel práctico, la resolución de problemas cambia la sistematización de las tareas de aprendizaje. Fomenta la aproximación de los contenidos curriculares a situaciones prácticas. Permite que se realicen múltiples repasos de los mismos contenidos y tareas. Y lleva consigo el desarrollo de habilidades generales para la vida, tales como la motivación y la perseverancia en la actividad, el desarrollo de estrategias específicas y la comprobación de la solución obtenida y el producto del trabajo (^{Suazo et al., 2022}).

De esta forma, el alumno consigue una comprensión más profunda de los procedimientos y las técnicas empleadas en cada dominio del currículo. Y comprende que cada resultado matemático alcanzado supone una consecuencia. Este esquema del proceso de resolución de problemas es el que late en el análisis cuando el sujeto examina la situación dada y realiza un plan. La resolución consciente de problemas matemáticos en los que intervienen operaciones, procedimientos o razonamientos. El esquema queda patente cuando el estudiante es objetivamente capaz de: extrapolar secuencias espaciales o numéricas, clasificar o relacionar objetos, comprender, organizar o estructurar conceptos no rutinarios, resolver situaciones auténticas en las que los aspectos matemáticos son no evidentes, aplicar algoritmos, procedimientos o razonamientos (^{Tejero Alegre, 2024}).

Así mismo, se destacan diversas investigaciones entre las que se encuentra el trabajo de ^{Montilla-García (2022)} en diseño cuantitativo, ya que se parte de una observación sobre la relación entre el pensamiento sistémico y la resolución de problemas en estudiantes de secundaria, mediante un modelo basado en el pensamiento sistémico, se consigue la eficiencia en la resolución de problemas matemáticos complejos. Este modelo consta de tres procesos: primero, desde el proceso de resolución del problema planteado, luego, desde el proceso de decisión hacia la construcción de la solución y propiamente, hacia la concretización de la solución al problema, donde esta se resuelve por medio de procedimientos formalizados, que a su vez se concretizan por un software para la simulación dinámica.

Seguidamente ^{Conforme Holguín y Mendoza Moreira 2022}: argumentan realizar el análisis de las estrategias didácticas creativas, que los docentes emplean para la resolución de problemas; así como, el análisis de la etapa del nivel del pensamiento lógico-matemático alcanzada por los adolescentes. Al respecto, observan que es necesario enseñar de alguna manera las estrategias didácticas; ya que, los docentes de la educación primaria y secundaria, pueden enseñar de manera diversa los contenidos matemáticos, instruyendo un conocimiento sustentativo por construcciones. En esta investigación se asumió que al ser estimulado al aprendizaje de las matemáticas a una muy corta edad, será más fácil para los jóvenes al resolverse los problemas de la vida diaria.

De manera similar, ^{Ledo-Miralles et al. (2020)} propusieron un método heurístico para resolver problemas matemáticos a partir de texto en su estudio. A partir de las necesidades y métodos de docentes y estudiantes, este estudio ofrece sugerencias encaminadas a decodificar el texto y resolver problemas a través de heurísticas de procesos y de enseñanza, las cuales deben señalarse de acuerdo con el uso teórico y la sistematización empírica del autor.

Asimismo, ^{Arteaga-Martínez et al. (2020}) examinaron la importancia de resolver problemas matemáticos mediante un cambio metacognitivo. En términos de compromiso, es la comprensión del contenido a partir del proceso de pensamiento y la conexión, análisis, percepción, discusión, sabiduría, coraje, libertad, etc. que todos los estudiantes deberían tener. incluye habilidades y habilidades. Permite conocimientos tanto generales como detallados para afrontar situaciones difíciles y garantizar el éxito. En su estudio, ^{Buchholtz (2021)} intentó determinar los patrones utilizados por los estudiantes al resolver problemas numéricos; Un aporte importante a las matemáticas que se enseñan en el aula.

En su estudio, ^{Poveda Fernández (2020)} pretende analizar la calidad y el tiempo que proporciona GeoGebra en el proceso de resolución de problemas y concluye que es posible crear una representación del problema, porque este enfoque permite analizar el contenido que surgir más tarde. disponible. La base para la toma de decisiones basada en las propiedades matemáticas presentes en la configuración y sus relaciones o diferencias.

Del mismo modo, ^{Gualdrón et al. (2020)} destacan la importancia de las orientaciones a los docentes del área de matemática, acerca de la planificación de sus sesiones de aprendizaje, las cuales deben estar contenidas por actividades lúdicas, recreativas e innovadoras, incluyendo el método Pólya, el cual permitirá reflexionar, experimentar, comunicar y tomar decisiones.

De manera similar, ^{Cuello Alean et al. (2020)} llevaron a cabo una investigación para comprobar el efecto de las estrategias de entretenimiento en el desarrollo de habilidades de resolución de problemas matemáticos. Un aporte importante es que esta investigación representa el desarrollo de habilidades de resolución de problemas matemáticos; debido a que aprender es divertido, los estudiantes pueden colaborar, expresarse, hacer tareas y participar en temas similares; Con la estrategia de planificación, los estudiantes han encontrado una buena manera de aprender y resolver problemas.

Igualmente, ^{Valbuena Duarte et al. (2020)} se aproxima al objeto de estudio de forma cualitativa; logrando profundizar sobre el sistema de argumentación matemática en el accionar docente, realizando una aproximación global de situaciones problemáticas; luego del análisis de los resultados; el estudio concluye que las matemáticas para ser aprendidas, dependen de la participación del estudiante en el proceso de argumentación, permitiendo así la descripción de las diferentes etapas de resolución del problema. De allí la importancia que en el aula se genere un ambiente reflexivo tanto en el docente como en los estudiantes.

Finalmente, ^{Martin-Requejo et al. (2023)}, analiza las relaciones existentes entre la resolución de problemas y las funciones ejecutivas, inteligencia emocional, los hábitos y técnicas de estudio. Se evidencia que, por cada habilidad matemática, existen diferentes procesos neuropsicológicos; por lo que se hace necesario intervenir de manera diferenciada; para ello se debe emplear programas orientados a fomentar el aprendizaje matemático, en función a las dificultades que se encuentren de manera específica en cada estudiante.

La resolución integrada de problemas incluida en el currículo escolar no es nueva en la educación matemática, tal y como se ha considerado desde civilizaciones antiguas como la griega o la romana, donde formaba parte de temas de investigación (^{Arteaga-Martínez et al., 2020}).

Por su parte, ^{Lesh y Zawojewski (2007)}, p. 782) explica la resolución de problemas de la siguiente manera

“[...] el proceso de interpretar una situación matemáticamente, la cual involucra varios ciclos interactivos de expresar, probar y revisar interpretaciones, de ordenar, integrar, modificar, revisar o redefinir grupos de conceptos matemáticos desde varios tópicos dentro y más allá de las matemáticas.”

En este sentido, para resolver el problema, el estudiante debe realizar un proceso compuesto por diferentes pasos que le permitan recopilar, organizar y analizar información para utilizar estrategias que le permitan encontrar una solución. En lo que respecta a la resolución de problemas, la gestión metacognitiva promueve la comprensión y la búsqueda de formas de resolver problemas de manera efectiva y emocional; Estudios anteriores han demostrado que las estrategias metacognitivas añaden valor al proceso de formación voluntaria y resolución de problemas (^{Desoete, 2007}).

En el proceso de la revisión sistémica, acerca de la resolución de problemas, ^{Torregrosa et al. (2020)}, afirma que estos procesos metacognitivos se encuentran en el centro de la matemática, por lo que resulta ser esencial en la educación. En la perspectiva de ^{Pérez y Ramírez (2008)}, la resolución de problemas matemáticos exige la adaptación de los estudiantes a situaciones diversas de la propia vida, con el fin de responder adecuadamente ante ellas. Para ^{Bruning et al.(2012)} la enseñanza de la matemática es una tarea con alta complejidad donde están implicados varios factores, como la adquisición de destrezas y procedimientos; además de la comprensión de los conceptos y principios.

Es de gran importancia el rol que cumple el pensamiento lógico matemático; puesto que integra el conocimiento lógico y físico asimilado por los individuos, resultado de la experiencia que se adquiere en el manejo de las cosas cotidianas y simples (^{Reyes Fernandez, 2021}).

A decir de ^{Huijsmans et al. (2022)}, la resolución de problemas requiere una atención de manera individual por estudiante; para ello, se hace necesario la combinación realizada entre el aprendizaje cooperativo y el adiestramiento de estrategias que se orientan a la resolución de problemas matemáticos paso a paso; planteamiento que se verifica en la propuesta pedagogica realizada por ^{Klang et al. (2021)}.

El aprendizaje que se basa en problemas reales y complejos se considera un método de enseñanza innovador, mediante que promueven autoaprendizaje de manera colaborativa, teniendo como protagonistas a los estudiantes (^{Universidad Politecnica de Madrid, 2022}).

Para la resolución de problemas, se debe buscar acciones para su abordaje, aunque no necesariamente conduzcan de manera directa al objetivo; esto significa que se debe transitar por un proceso, donde se puede reajustar y reformular la problemática para poder comprender mejor (^{Cobeña Moreira y Cedeño Loor, 2023}). Del mismo modo, existe una gran influencia de la comprensión lectora en la resolución de problemas (^{Cristobal Terrones et al., 2023}). Al respecto ^{Alvarado Guerra (2023)} menciona que es de gran trascendencia que en las escuelas exista la integración del área de comunicación en la resolución de problemas matemáticos.

Además, la resolución de problemas implica analizar la lógica de las matemáticas para que los estudiantes puedan explorar las múltiples aplicaciones de este campo en la vida diaria y tomar decisiones importantes (^{Quiñones Vásquez, y Huiman Tarrillo, 2022}). Es importante señalar que los docentes deben asumir el liderazgo, tener responsabilidad en el desarrollo del pensamiento. El rol de socio y guía que otorga capacidad de resolución de problemas en el proceso (^{Ricardo-Fuentes et al., 2023}).

CONCLUSIONES

En la actualidad, el docente se encuentra ante diferentes problemas matemáticos, es por esto que debe promover desde edades tempranas el desarrollo en el estudiantado de estrategias que le permitan enfrentarse de la mejor forma posible a la resolución de los mismos. Por esto, resulta imprescindible conocer las estrategias y los procedimientos que utilizan los estudiantes a la hora de resolver un problema matemático, puesto que se conocen escasos o nulos trabajos en la literatura, donde se aborde este enfoque en las Guías Educativas de año 1 encuentro edades comprendidas entre 5 y 6 años.

Los resultados obtenidos en esta investigación resaltan la importancia de formular recomendaciones educativas que brinden apoyo cognitivo, actitudinal y emocional en el ámbito de las matemáticas, especialmente para abordar los problemas identificados. Para ello, será fundamental definir, estructurar y diseñar metodologías que permitan matematizar situaciones de la vida real, es decir, formular problemas de manera matemática.

En consecuencia, se recomienda llevar a cabo programas de formación que consideren tres aspectos clave:

En primer lugar, es importante tener en cuenta a los estudiantes y sus conocimientos previos. Cada estudiante tiene una base única de conocimientos y experiencias en matemáticas, por lo que es esencial diagnosticar y comprender sus necesidades individuales. Esto permitirá diseñar estrategias de enseñanza que se ajusten a su nivel de comprensión y les brinden el apoyo necesario para avanzar en su aprendizaje. Además, es crucial abordar las actitudes negativas hacia las matemáticas, fomentando un ambiente positivo y motivador que promueva la confianza y el interés en la materia.

En segundo lugar, los profesores desempeñan un papel clave en la mejora de la enseñanza de las matemáticas. Es necesario proporcionarles programas de formación continua que los capaciten en metodologías de enseñanza efectivas y actualizadas. Los docentes deben estar familiarizados con enfoques pedagógicos innovadores y recursos didácticos que promuevan el aprendizaje activo y significativo de las matemáticas. Esto implica utilizar diferentes herramientas y tecnologías, realizar actividades prácticas y fomentar la resolución de problemas en colaboración.

Por último, los aspectos curriculares también deben ser considerados. El currículo de matemáticas debe ser revisado y adaptado para incluir situaciones de la vida real que motiven a los estudiantes y les permitan aplicar los conceptos matemáticos en contextos concretos. Esto implica vincular las matemáticas con otras disciplinas y áreas de estudio, destacando su relevancia en la resolución de problemas del mundo real. Además, se deben establecer objetivos claros que vayan más allá de la mera memorización de fórmulas y procedimientos, buscando desarrollar habilidades de pensamiento crítico, razonamiento lógico y resolución de problemas.

En conclusión, mejorar la enseñanza y el aprendizaje de las matemáticas requiere un enfoque holístico que considere a los estudiantes, los profesores y los aspectos curriculares. Al formular recomendaciones educativas que aborden estos tres pilares, se promoverá un cambio positivo en la forma en que se enseña y se aprende matemáticas, fomentando una mayor comprensión, aplicación y aprecio por esta disciplina en los estudiantes.