ESTUDIO DEL COMPORTAMIENTO DE ESTRUCTURAS FABRICADAS CON METAL EXPANDIDO SOMETIDAS

A COMPRESIÓN AXIAL

 Dimas Smith¹, Carlos Graciano², Gabriela Martínez²

1 Departamento de Mecánica y Tecnología de la Producción, Universidad Nacional Experimental Francisco de Miranda, Falcón, Venezuela. Email: dimas.smith@gmail.com

2 Departamento de Mecánica, Universidad Simón Bolívar, Apdo. 89000, Caracas 1080-A, Venezuela.

RESUMEN

Una lámina de metal expandido es fabricada convencionalmente de una lámina de metal que es cortada y estirada (expandida) para formar una estructura con intersticios. (Mulder, 2005). Cuando se expande el metal se forma un patrón de celdas similar a un diamante el cual está caracterizado por dos ejes geométricos. Este producto puede ser usado para pasarelas, aplicaciones eléctricas, vallas de seguridad, propósitos decorativos y también como refuerzo para concreto. Actualmente el metal expandido es usado para aplicaciones estructurales, sin embargo poca información puede encontrarse en relación al comportamiento estructural de elementos fabricados con metal expandido. Este artículo tiene como objeto estudiar el colapso axial de tubos cuadrados y circulares fabricados con láminas de metal expandido bajo cargas compresivas a fin describir el comportamiento global de estas estructuras. Ensayos de compresión cuasi-estáticos fueron realizados a temperatura ambiente en una máquina MTS a fin de investigar la influencia del ángulo formado entre el eje mayor de la lámina de metal expandido y la dirección de la carga. De los resultados, tres tipos de respuesta de colapso se observó en función de la orientación de los ejes: (1) Modo 1 caracterizado por un mecanismo de colapso plástico; (2) Modo 2 pandeo local de las celdas individuales; y (3) Modo 3 pandeo global de las paredes de los tubos.

 Palabras clave: Láminas de Metal Expandido, Absorción de Energía, colapso axial.

STUDY OF THE BEHAVIOUR OF STRUCTURES MADE WITH EXPANDED METAL UNDER AXIAL COMPRESSION

ABSTRACT

A sheet of expanded metal is conventionally fabricated from sheet metal that is slit and stretched (expanded) to form a structure with interstices. (Mulder, 2005). When expanding the metal a diamond like cell pattern is formed which is characterised by two geometrical axes. This product can be used for catwalks, electrical applications, safety fences, decorative purposes and also as reinforcement for concrete. Currently expanded metal is used for structural application, however little information can be found regarding the behavior of structural elements made of expanded metal. The aim of this paper is to study the axial collapse of square and round tubes made of expanded metal sheet under compressive loading to describe the global behavior of these structures. Quasi-static compression tests were performed at room temperature in a MTS machine in order to investigate the influence of the angle formed between the major axis of the expanded metal and the load direction. From the results, three types of collapse response were observed depending on the orientation of the axes: (1) Mode 1 characterized by a plastic collapse mechanism; (2) Mode 2 local buckling of the individual cells; and (3) Mode 3 global buckling of the tube walls.

Keywords: Expanded Metal Sheets, Energy Absorption, axial collapse

Recibido: 18/11/09 Revisado: 28/03/09 Aceptado: 16/04/09

1. INTRODUCCIÓN

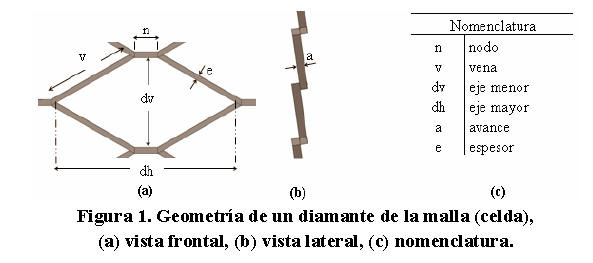
 El metal expandido es un material en forma de malla fabricado convencionalmente de una lámina de metal lisa que es cortada y estirada perpendicularmente hasta alcanzar un ángulo máximo de 90º para formar una geometría con aberturas que tienen substancialmente forma romboidal. (Figura 1). Como el proceso de manufactura de estas láminas es bastante económico y las mismas pueden ser cortadas fácilmente, es común encontrar este tipo de mallas en diversas formas y aplicaciones (Mulder, 2005). El corte y la deformación plástica producida en estas láminas permite generar un área final de hasta diez (10) veces su tamaño inicial y reducir su peso por metro cuadrado hasta en un 80% en comparación con las láminas sólidas (Sánchez y Graciano, 2005).

A pesar de que el uso de láminas de metal expandido para aplicaciones estructurales data de hace más de cien años (Storck, 1894) y aún cuando diversos autores entre los que destacan Aalberg y Haugen, 1997; Hellsten, 1998a: Hellsten 1998b; Oliveira et al., 2002; Bergey, 2002; Sánchez y Graciano, 2005; Escalona, 2005; Kooistra y Wadley, 2005; Ayestarán et al., 2006; Jitaru y Cristescu, 2007; entre otros, se han abocado a investigar numérica y experimentalmente su aplicabilidad en este campo, la información por estos métodos aún es escasa. Esto ha motivado el desarrollo de esta investigación con la cual se pretende aportar información experimental para caracterizar el comportamiento estructural de perfiles de sección cuadrada y circular fabricados con láminas de metal expandido sometidos a cargas de compresión axial cuasi-estáticas. Esto con el fin de analizar su respuesta cuando se produce una variación en la orientación y dirección de las celdas.

2. ENSAYOS EXPERIMENTALES

A continuación se presentan los procedimientos utilizados para el estudio del comportamiento estructural de las geometrías analizadas (cuadrada y circular) que fueron fabricadas con láminas de metal expandido en diferentes orientaciones con respecto a los ejes geométricos de las celdas. De esta forma se pretende generar experimentalmente modelos que ayuden a explicar y predecir la forma en la cual se desempeñarán estos elementos estructurales cuando son sometidas a cargas compresivas. Para ello se tomó en consideración la metodología sugerida por la Norma utilizada para ensayos mecánicos de compresión ASTM E9 89a (2000). 2.1 Materiales y métodos El metal expandido fue fabricado y suministrado por la empresa Maboca C.A. La Tabla 1, muestra la designación de la malla de metal expandido utilizada en este trabajo, cuyas dimensiones generalmente se presentan en láminas de 1,20 m x 2,44 m, en una amplia variedad de calibres. Las especificaciones comerciales del acero seleccionado se muestran en la misma tabla. A fin de investigar el comportamiento anisotrópico de las mallas de metal expandido sometidas a compresión axial, se obtuvieron las curvas de carga-desplazamiento de dos (02) modelos con diferentes secciones transversales. El Modelo “A” con sección transversal cuadrada de 110x110 mm por lado y el Modelo “B”, de sección transversal circular con un diámetro exterior de 120 mm. (Figura 2). Para la fabricación de las probetas de sección cuadrada se tuvo cuidado especial de forma tal que cada una de las caras quedara paralela entre sí. (Figura 2a).

 

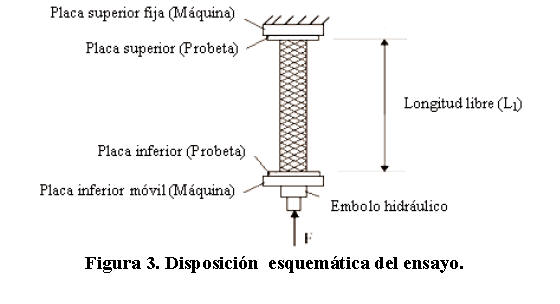
Las probetas correspondientes a ambas geometrías fueron cortadas a una longitud (L1) de 400 mm con un equipo de plasma Cutting System Econo-Pack 25 ® Modelo Econopak 25 (10 Amp, 50/60 Hz, 220 Volts, 50 Psi) debido a que éste generaba un corte preciso y una zona de afectación por calor bastante menor. Los extremos de las probetas fueron maquinados para proporcionar una superficie plana en el contacto con la placa superior e inferior que fueron soldadas a las mismas. En la Figura 3 se muestra un esquema de la disposición del ensayo. Todas las probetas se conformaron mediante soldadura por arco eléctrico con electrodos E/6013 de 32" 3 diámetro. Se utilizó una máquina Miller Electric MFG, Modelo 250 AC/DC. Este tipo de soldadura aun cuando requiere de la limpieza de las escorias en los puntos de unión, presentó buen acabado superficial y resistencia por lo cual no fue necesario limpiar. Debe destacarse que a pesar de que en los puntos de soldaduras ocurren cambios en la microestructura y consecuentemente en las propiedades mecánicas del material, a nivel general no se observó una influencia significativa de las mismas. Esto se pudo apreciar en la simetría de muchos de los patrones de deformación de algunas probetas.

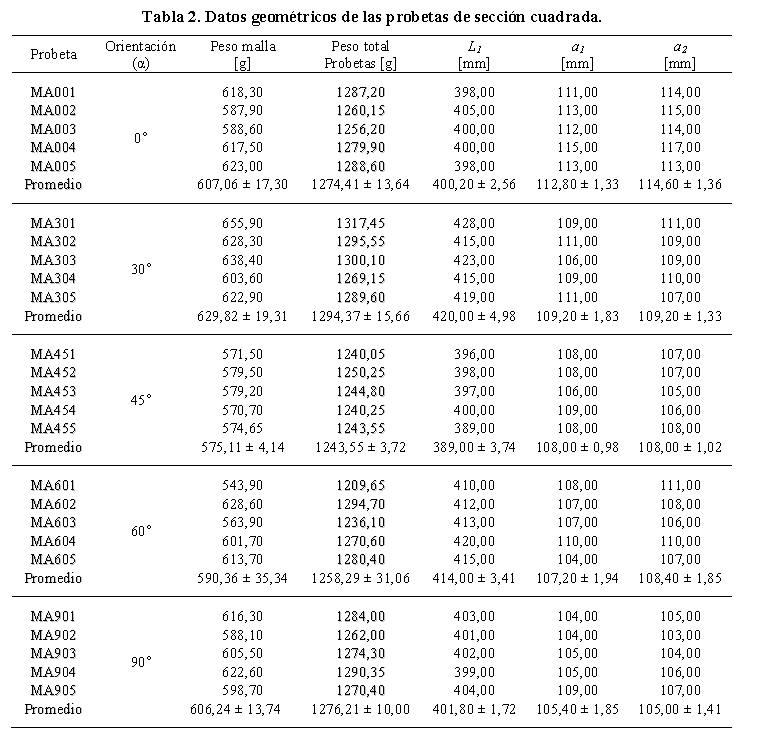
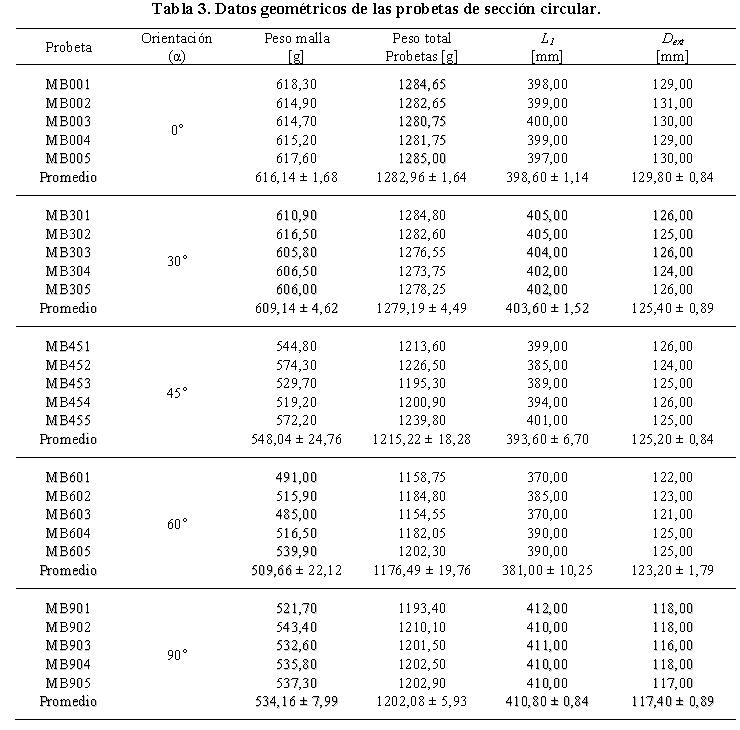
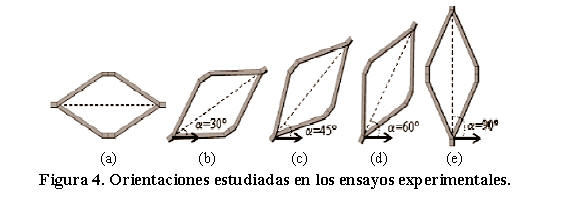
Las probetas fueron designadas y numeradas de acuerdo a tres (03) variables: modelo a ensayar, ángulo de orientación de la lámina de metal expandido y número del ensayo. Así MA001 indica el Modelo “A” ensayado a un ángulo α= 0.0º en el primer ensayo: mientras que MB302 significa que el Modelo “B” fue ensayado a una orientación de 30º en el segundo ensayo (repetido). En la Tabla 2 y Tabla 3, se presentan los datos geométricos para los modelos con sección transversal cuadrada y circular utilizados en las diferentes orientaciones. En cada modelo se estudió el modo de colapso y la influencia de la orientación de la malla sobre la capacidad de absorción de energía, pudiéndose así establecer las respectivas comparaciones entre ambas geometrías. Las orientaciones fueron estudiadas para los ángulos α= 0°, 30°, 45º, 60° y 90° (Figura 4), siendo el ángulo α=0° la dirección definida cuando el eje mayor es paralelo al plano horizontal de referencia.

Todas las probetas se ensayaron a temperatura ambiente en la máquina de Ensayos Mecánicos Modelo MTS, de 25 toneladas de capacidad, que se encuentra en el Laboratorio “E” de la Universidad Simón Bolívar a una velocidad de desplazamiento controlado del pistón de 05 mm/min.

2.2 Resultados Se presentan las curvas carga-desplazamiento para las cinco (05) probetas ensayadas en cada orientación. Se verificó en la mayoría de las curvas obtenidas para un mismo tipo de ensayo que se producen pequeñas variaciones en la respuesta de la carga en función del desplazamiento. Durante el aplastamiento estático de ambas geometrías, conforme a lo expresado por Mamalis et al. (1989), no se consideraron los efectos elásticos iniciales debido a que la energía plástica disipada en las probetas fue considerablemente mayor que la energía elástica de deformación. De igual manera en concordancia con lo formulado por Alghamdi (2001) la respuesta de pandeo inicial tampoco fue considerada desde un punto de vista de absorción de energía. En tal sentido se analizó el comportamiento post-pandeo, el cual está asociado a grandes deflexiones y deformaciones. Además de describir los diversos mecanismos de colapso plástico generados en los modelos estudiados se analizaron parámetros de comportamiento estructural como energía absorbida, carga media de colapso y eficiencia estructural, todo esto para caracterizar la capacidad de absorción de energía por deformación plástica de estos elementos. La energía total disipada (Ea) se obtuvo mediante la integración del área bajo la curva carga-desplazamiento.

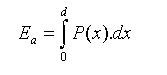
Como una medida adicional para comparar la eficiencia de absorción de energía de los modelos estudiados y como un parámetro de diseño en sistemas limitados por el peso se consideró de acuerdo a Huang et al. (2002) y Hosseinipour y Daneshi (2003) la energía absorbida por unidad de masa deformada. Asimismo se determinó la carga media de colapso (Pm) a través de la integración de la carga constante equivalente medida sobre la deformación de la sección (Tarigopula et al, 2005), donde Ea representa la energía total disipada, P(x) representa el valor de la carga y d representa la longitud total de desplazamiento. La carga media se define como:

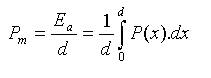
Finalmente a fin de comparar las capacidades de los distintos modelos sometidos a cargas de aplastamiento axial, se consideró según Olabi et al. (2007), un factor de eficiencia estructural dado por la relación:

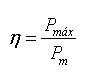
2.2.1 PROBETAS DE SECCIÓN CUADRADA.

2.2.1.1 Ensayo en la orientación α=0°

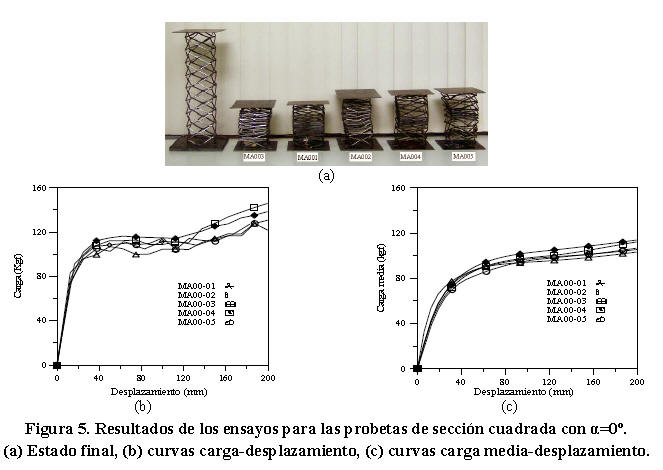
En este ensayo la dirección de la carga coincide con el eje geométrico menor (dv) del diamante de la lámina de metal expandido. (Figura 4a). En la Figura 5a, se muestra el estado final para las probetas de sección cuadrada en la orientación α=0º. Las curvas carga-desplazamiento y carga media-desplazamiento de las cinco (05) probetas ensayadas son mostradas en las Figuras 5b y 5c.

En la Figura 5b, inicialmente se observa que todas las curvas exhiben una transición suave del dominio elástico al plástico, verificándose que al alcanzar la carga máxima (Pmáx=112,08 ± 4,08 Kgf) se producen grandes desplazamientos sin un aumento apreciable de carga. Una vez que las probetas alcanzan un desplazamiento de 120 mm, comienzan a generarse ajustes en la geometría de las mismas muy cerca de la sección media que hacen que en los nodos de las celdas se formen zonas de plastificación (rótulas plásticas) que provocan un aumento en la rigidez de las celdas y esto a su vez, un incremento progresivo de la carga con grandes desplazamientos. Se observa también una respuesta uniforme y controlada en las curvas generadas por estas probetas. En la Figura 5c, se observa que la mayoría de las curvas obtenidas para un mismo tipo de ensayo presentan pequeñas variaciones en la respuesta de la carga media en función del desplazamiento. Insignificantes diferencias en los niveles de carga en función del desplazamiento se observan en las Figuras 5b y 5c, lo cual indica que la capacidad de estos elementos estructurales para aplicaciones de absorción de energía es aceptable.

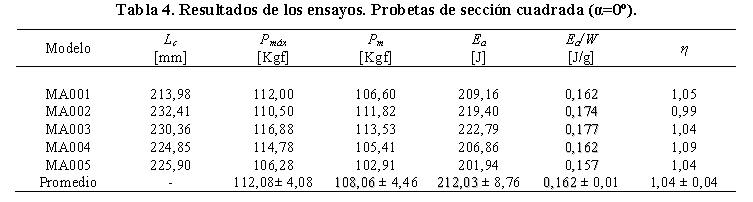
En la Tabla 4, se presenta información sobre el desplazamiento final, carga media de colapso, energía absorbida y factor de eficiencia estructural en cada una de las probetas ensayadas. Los resultados de la Tabla 4, muestran que para un nivel desplazamiento de 200 mm, el promedio de energía absorbida y carga media de colapso en estas probetas fue 212,03 ± 8,76 J y 108,06 ± 4,46 Kgf respectivamente. Cuando se consideró la energía absorbida por unidad de peso el valor registrado fue 0,162 ± 0,01 J/g. En relación al promedio del factor de eficiencia estructural reportado se observa que el mismo fue muy cercano a uno (η=1,04 ± 0,04) lo cual evidencia que la carga máxima Pmáx alcanzada por las probetas en esta orientación fue aproximadamente igual a la carga media Pm. Este valor, en términos de absorción de energía, indica que la respuesta de estas probetas fue estable.

2.2.1.2 Ensayo en la orientación α=30°

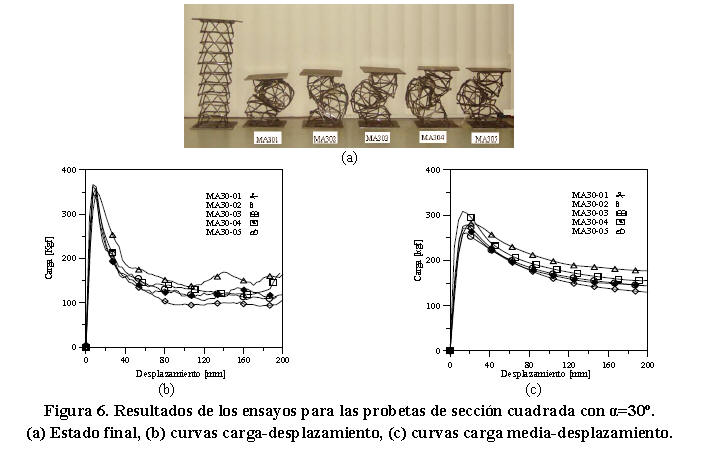
En este ensayo el eje geométrico de la lámina de metal expandido forma 30º con el plano horizontal de referencia (Figura 4b). En esta orientación los ejes del material presentan la mayor inclinación en relación a la dirección de aplicación de la carga. La Figura 6a muestra el estado final de las probetas. Las Figuras 6b y 6c, muestran respectivamente las curvas carga-desplazamiento y carga media  desplazamiento de los modelos estudiados.

En la Figura 6b puede observarse que las curvas obtenidas de los cinco (05) ensayos presentan un incremento progresivo hasta alcanzar una carga máxima promedio de 367,65 ± 10,53 Kgf (aprox. 3,5 veces mayor a la carga máxima obtenida por las probetas de sección cuadrada estudiadas en la orientación α=0º). Luego se produce una caída súbita en la capacidad de carga de las mismas con grandes desplazamientos. Este comportamiento está asociado al hecho de que cuando se alcanza la carga máxima, las venas de las celdas ubicadas en el eje del material próximas a la sección intermedia de las probetas, tiendan a cerrarse provocando que el elemento pierda estabilidad y en consecuencia hacen que la capacidad de carga que puede soportar la estructura se reduzca considerablemente. En la Figura 6c, se observa que en esta orientación la capacidad de absorción de energía de estos modelos se incrementa (en comparación con la orientación α=0°), lo cual también contribuye a aumentar la carga media. Este comportamiento está asociado a las inestabilidades causadas por el pandeo local de las celdas y al fenómeno de rotación que se produce en estos modelos. En la Tabla 5, se muestran los resultados obtenidos en este ensayo. Como se observa el promedio de energía absorbida y carga media de colapso para estas probetas fue 305,00 ± 40,93 J y 155,43 ± 20,85 Kgf, lo que representa un incremento de 65% y 44% respectivamente en relación con las probetas de sección cuadrada estudiadas en el caso anterior. Un incremento similar se presentó en estos modelos en la energía absorbida por unidad de peso cuyo valor registrado fue 0,236 ± 0,03 J/g. El promedio del factor de eficiencia estructural obtenido para estas probetas fue 2,37 ± 0,26.

2.2.1.3 Ensayos en la orientación α=45º.

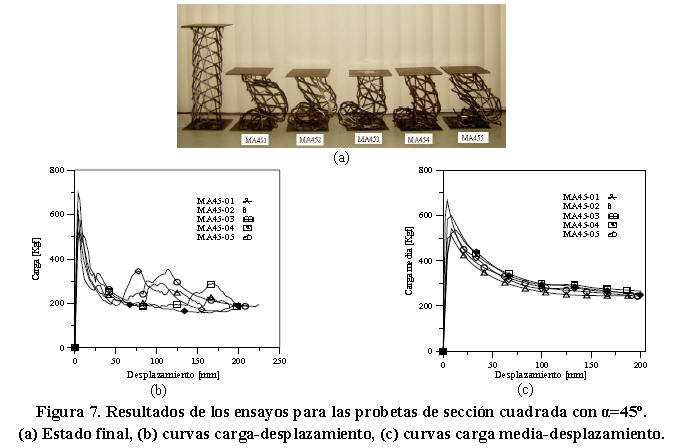
Para esta orientación la dirección de aplicación de la carga forma 45º con el eje geométrico de la lámina de metal expandido (Figura 4c). En la Figura 7a se muestra el estado final de las probetas para esta orientación. Las Figuras 7b y 7c presentan las curvas carga-desplazamiento y curvas carga media desplazamiento para cada ensayo.

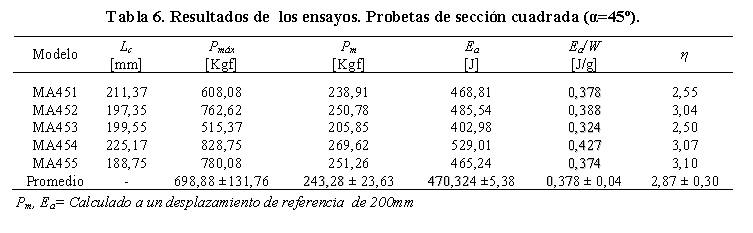
Como se observa en la Figura 7b, la capacidad de carga de las probetas disminuye bruscamente una vez que alcanzan la carga máxima (Pmáx=698,98 ± 131,76 Kgf). Para desplazamientos superiores a 50 mm, se generan pequeños picos de carga que se repiten. Estos picos evidencian que el comportamiento de estas probetas en el régimen plástico es bastante inestable. En la Tabla 6 se presentan los resultados obtenidos en este ensayo. El promedio de energía absorbida y carga media de colapso para estas probetas fue de 470,32± 5,38 J y 243,28 ± 23,63 Kgf respectivamente. La energía absorbida por unidad peso se registró en 0,378 ± 0,04 J/g. El promedio del factor de eficiencia estructural fue de 2,87 ± 0,30.

2.2.1.4 Ensayos en la orientación α=60º.

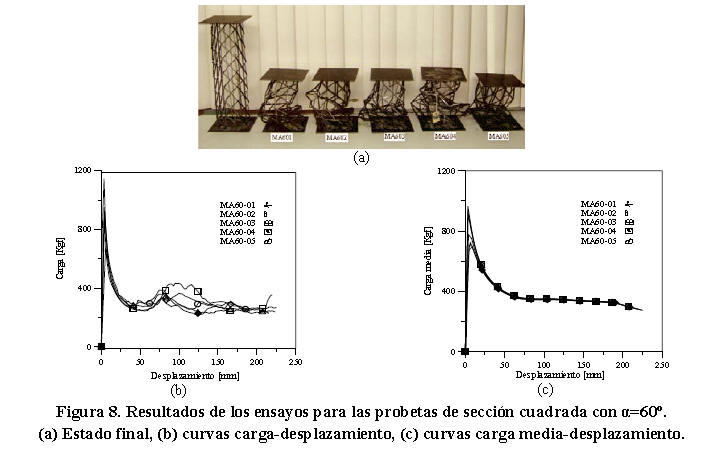
En este ensayo la dirección de aplicación de la carga coincide con la orientación del eje del material y las venas se comportan como columnas verticales (Figura 4d). En la Figura 8a se muestra el estado final para las probetas de sección cuadrada estudiadas en la orientación α=60º. Las Figuras 8b y 8c presentan respectivamente las curvas carga-desplazamiento y curvas carga media-desplazamiento para cada probeta analizada.

En la Figura 8b se observa que las curvas obtenidas en este ensayo presentaron el mayor incremento de carga máxima (Pmáx=1064,24 ± 164,97 Kgf) con la mayor disminución de la misma (Aprox. 80%). En la Figura 8c se evidencia un comportamiento similar para la curva carga media desplazamiento, evidenciando grandes las inestabilidades estructurales de estos elementos para esta orientación de las celdas. En la Tabla 7, puede observarse que el promedio de energía absorbida y carga media de colapso en las probetas estudiadas para esta orientación fue 605,55 ± 27,68 J y 311,78 ±14,49 Kgf respectivamente, siendo dichos valores los máximos reportados para las probetas de sección cuadrada. Esta tendencia fue consistente cuando se consideró la energía absorbida por unidad de peso computándose dicho valor en 0,481 ± 0,02 J/g. El promedio del factor de eficiencia estructural (η=3,41 ± 0,39) registrado en estos ensayos permite comprobar que las probetas estudiadas en esta orientación presentan una gran desventaja en términos de absorción de energía de impacto. Como se evidencia, a medida que el factor de eficiencia aumenta, el elemento se hace más inestable.

2.2.1.5 Ensayos en la orientación α=90º

En este ensayo la dirección de la carga coincide con el eje geométrico mayor (dh) de la lámina de metal expandido (Figura 4e). La Figura 9a muestra el estado final de las probetas para esta orientación. La Figuras 9b y 9c muestran respectivamente las curvas carga-desplazamiento y las curvas carga media desplazamiento para cada ensayo.

En la Figura 9b, se observa en estas curvas un comportamiento similar al presentado por las curvas estudiadas en las orientaciones previas (excepto para la orientación α=0º). Sin embargo en este caso al alcanzar la carga máxima (Pmáx=466,24 ± 13,57 Kgf) la disminución en la capacidad de carga para estas probetas fue la menos violenta, lo cual se atribuye a que el ajuste en la geometría de las celdas se orienta en la dirección más larga del diamante de la malla de metal expandido. En la Figura 9c, se observa que el aplastamiento de las celdas y la contribución de área adicional de trabajo se traducen en un aumento en la respuesta de carga media para estos modelos.

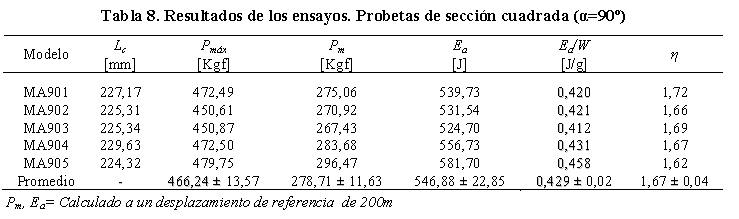
De la Tabla 8 se observa que el promedio de energía absorbida y carga media de colapso registrado para estas probetas fue 546,88 ± 22,85 J y 278,71 ± 11,63 Kgf respectivamente. Estos valores conjuntamente con los obtenidos en la orientación α=60º fueron los máximos registrados para estas geometrías. La energía absorbida por unidad de peso se computó en 0,429 ± 0,02 J/g. El promedio del factor de eficiencia estructural de las geometrías estudiadas se estimó en 1,67 ± 0,04.

2.2.2 PROBETAS DE SECCIÓN CIRCULAR Nota: Para estas geometrías se utilizaron las mismas orientaciones indicadas en la Figura 4.

2.2.2.1 Ensayos en la orientación α=0º

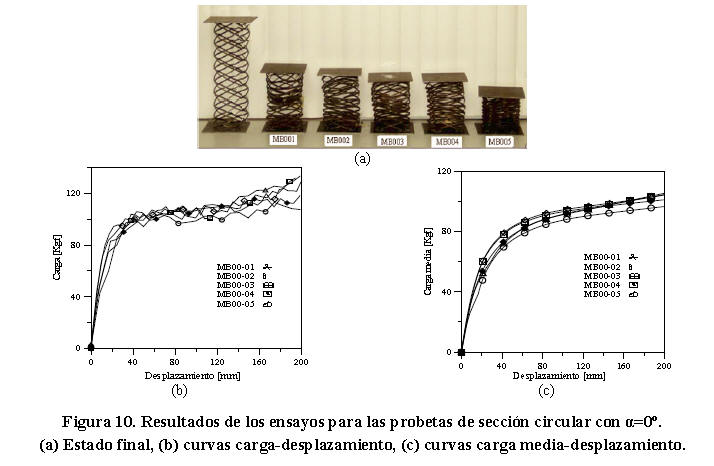
En la Figura 10a se muestra la geometría final para las probetas de sección circular. Las Figuras 10b y 10c muestran las curvas carga-desplazamiento y las curvas carga media-desplazamiento obtenidas para cada ensayo.

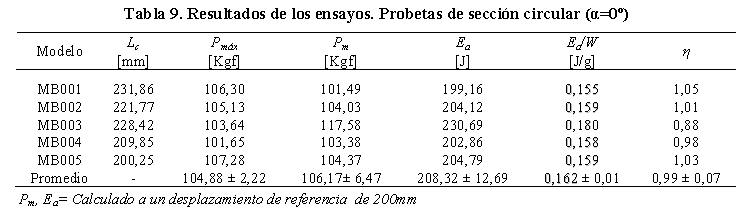
En la Figura 10b, se observa que las curvas exhiben un comportamiento similar al presentado por las probetas de sección cuadrada para la misma orientación. Al alcanzar la carga máxima (Pmáx=104,88 ± 2,22 Kgf) se evidencia un régimen estable de carga casi constante. Sin embargo para un desplazamiento aproximado de 125 mm se produce un leve aumento en la capacidad carga debido a los efectos generados por el contacto entre las celdas. Las insignificantes diferencias en los niveles de carga y carga media en función del desplazamiento en las Figuras 10b y 10c indican que la capacidad de estos elementos estructurales para aplicaciones de absorción de energía es estable. De la Tabla 9 se obtiene que la energía absorbida y carga media de colapso de las probetas para esta orientación fue 208.32±12,69 J y 106,17± 6,47 Kgf respectivamente. La energía absorbida por unidad de peso se registró en 0,162 J/g ± 0,01. El promedio del factor de eficiencia estructural en estas probetas arrojó un valor muy cercano a uno (η=0,99 ± 0,07), lo cual revela una respuesta favorable para que puedan emplearse en el diseño de dispositivos para aplicaciones de absorción de energía.

2.2.2.2 Ensayos en la orientación α=30º

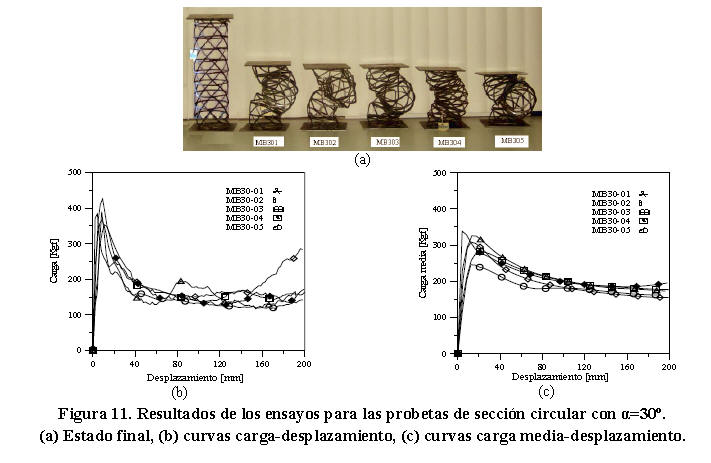
Las Figuras 11a, 11b y 11c muestran respectivamente el estado final, curvas carga-desplazamiento y curvas carga media-desplazamiento para las probetas estudiadas en esta orientación.

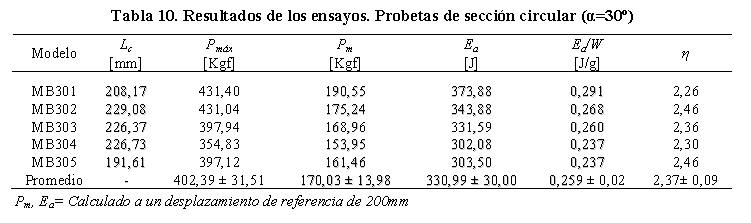
En la Figura 11b se observa que las curvas obtenidas en este ensayo presentaron un incremento considerable hasta alcanzar una carga máxima promedio de 402,39 ± 31,51 Kgf. Luego ocurre una reducción en la capacidad de carga hasta un desplazamiento aproximado de 60 mm. A partir de este punto se generan pequeñas fluctuaciones de carga como resultado del contacto entre las celdas y de diferentes secciones entre las probetas. En la Figura 11c, las curvas obtenidas reflejan que la energía absorbida y carga media de colapso alcanzada fue superior en 8% y 10% respectivamente en comparación con las probetas de sección cuadrada para la misma orientación. Este incremento está asociado a las inestabilidades causadas por el pandeo local de las celdas y al fenómeno de rotación que se produce en estos modelos. De la Tabla 10, se observa que el promedio de energía absorbida y carga media de colapso para estas probetas fue 331,00 ± 30,00 J y 170,03 ± 13,98 Kgf respectivamente. La energía absorbida por unidad de peso se computó en 0,259J/g ± 0,02. Dicho valor fue el máximo registrado en los ensayos para las probetas con sección circular. El promedio del factor de eficiencia estructural se estimó en 2,37 ± 0,09.

2.2.2.3 Ensayos en la orientación α=45º

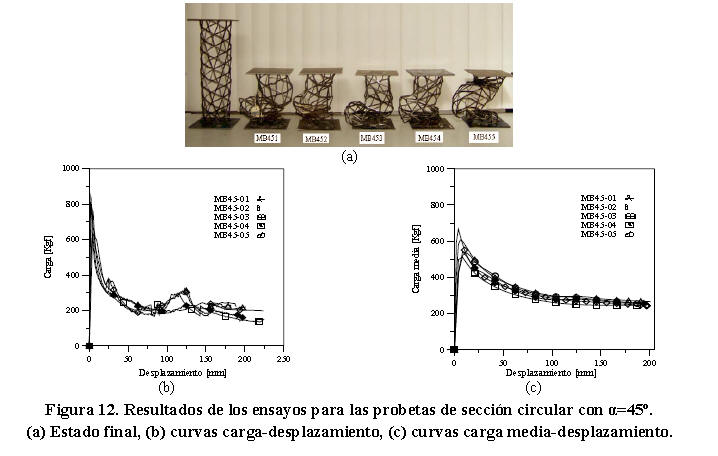
La Figura 12a muestra el estado final de las probetas de sección circular estudiadas en la orientación α=45º. Las Figuras 12b y 12c muestran las curvas carga-desplazamiento y las curvas de carga media-desplazamiento para cada ensayo.

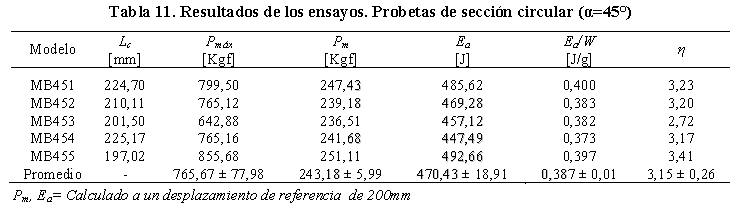
En la Figura 12b se observa que estas curvas exhiben un comportamiento similar al presentado por los modelos estudiados en la orientación anterior aún cuando la carga máxima alcanzada en este caso fue aproximadamente el doble y en el régimen plástico este modelo fue ligeramente más uniforme. Las curvas obtenidas se caracterizaron típicamente por presentar una reducción brusca en la capacidad de carga (una vez que se alcanzó la carga máxima Pmáx=765,67 ± 77,98 Kgf) seguida de leves incrementos de carga para desplazamientos superiores a 100 mm. Un comportamiento similar se observa en la Figura 12c, destacándose además un incremento aproximado de 42% en la carga media con respecto a la orientación anterior. En la Tabla 11, se muestran los resultados obtenidos en este ensayo. El promedio de energía absorbida, carga media de colapso y energía absorbida por unidad de peso obtenido para estas probetas fue de 470,43 ± 18,91 J; 243,18 ± 5,99 Kgf y 0,387 ± 0,01 J/g respectivamente. Los resultados anteriores difieren en menos del 1% en comparación con los valores registrados por las probetas de sección cuadrada para la misma orientación (Tabla 4.3). El factor de eficiencia estructural en estas probetas fue 3,15 ± 0,26.

2.2.2.4 Ensayos en la orientación α=60º

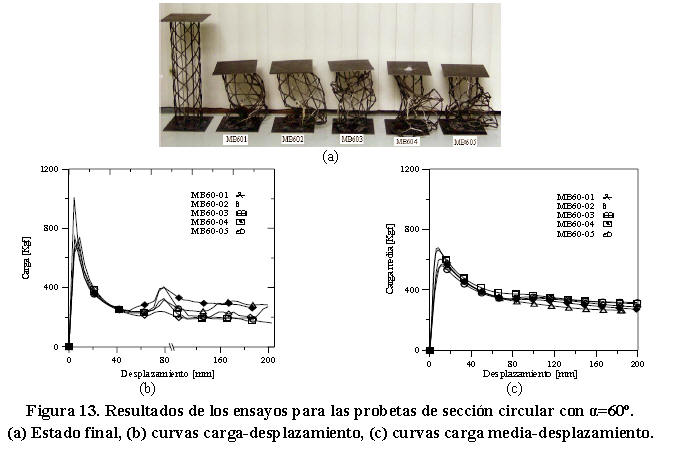
Las Figuras 13a, 13b y 13c muestran respectivamente el estado final, curvas de carga-desplazamiento y carga media-desplazamiento para las probetas de sección circular en la orientación α=60º.

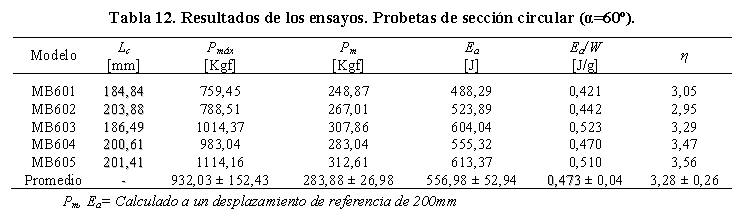
Las Figuras 13b y 13c muestran que las curvas obtenidas en este ensayo presentaron el mayor incremento en la carga máxima (Pmáx=932,03 ± 152,43 Kgf) y carga media (Pm=283,88 ± 26,98 Kgf). Contrariamente, estas curvas presentaron la mayor reducción de carga en los modelos estudiados, que en el caso de la carga máxima fue aprox. 80% y en el caso de la carga media fue de 30%. En la Figura 13b, se observa también que para un nivel de desplazamiento entre 75 mm y 175 mm ocurren leves variaciones de carga que disminuyen gradualmente. Estas variaciones, al igual que para las probetas de sección cuadrada con esta misma orientación, se producen por el contacto originado entre las celdas de las probetas. La Tabla 12, muestra que la energía absorbida y carga media de colapso registrada en las probetas de sección circular para esta orientación fue 556,98 ± 52,94 J y 283,88 ± 26,98 Kgf respectivamente. La energía absorbida por unidad de peso se computó en 0,473 ± 0,04 J/g. El promedio registrado para el factor de eficiencia estructural (η=3,28 ± 0,26) indica que la respuesta de estos modelos fue muy inestable.

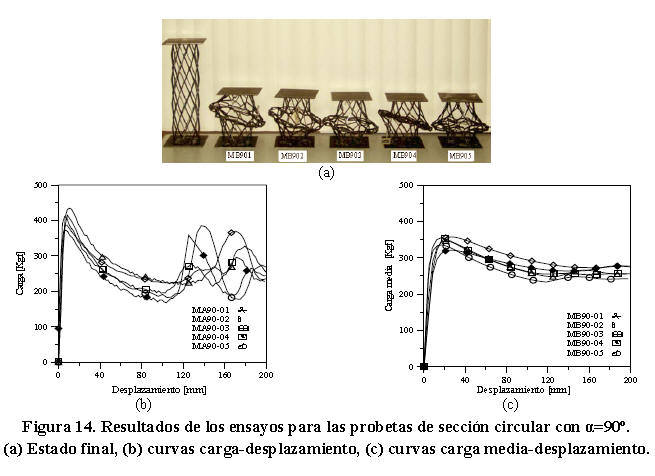
2.2.2.5 Ensayos en la orientación α=90º

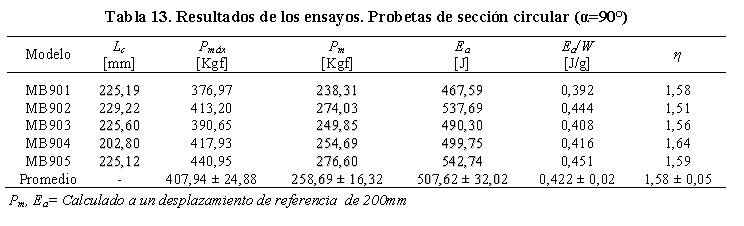
 La Figura 14a muestra la geometría final de las probetas de sección circular estudiadas en la orientación α=90º. Las Figuras 14b y 14c muestran respectivamente las curvas carga-desplazamiento y carga media de colapso-desplazamiento para cada ensayo. La Figura 14b muestra que el comportamiento de estas curvas fue similar al obtenido en las orientaciones α=30º, α=45º y α=60º para la misma geometría. Se observa que al alcanzar la carga máxima (Pmáx=407,94 ± 24,88 Kgf) la disminución en la resistencia estructural de estos modelos fue más controlada. Sin embargo para un desplazamiento superior a 100 mm, se evidencia un régimen plástico muy inestable con grandes fluctuaciones de carga en comparación con los modelos estudiados en las orientaciones previas. En la Figura 14c se registra que el comportamiento de las curvas carga media-desplazamiento también es bastante controlado una vez que alcanzan la carga máxima. Similar al modelo de sección cuadrada para la misma orientación a medida que el sistema continúa deformándose se adiciona área efectiva de trabajo que provoca un incremento de carga debido al aumento de rigidez en los nodos de las celdas. La Tabla 13, muestra los resultados de este ensayo. La energía absorbida y carga media de colapso en estas probetas se estimó en 507,62 ± 32,02 J y 258,69 ± 16,32 Kgf. Dichos valores fueron ligeramente inferiores a los obtenidos con las probetas de sección cuadrada para la misma orientación. La energía absorbida por unidad de peso fue de 0,422 ± 0,02 J/g. El promedio del factor de eficiencia estructural se calculó en 1,58 ± 0,05.

3. MECANISMOS DE COLAPSO

 A continuación se describen las secuencias de deformación de cada uno de los modelos estudiados en las diferentes orientaciones así como también el mecanismo de colapso de los mismos. Se observaron tres (03) modos de colapso: a) Modo 1, aplastamientos irregulares e inestables de las celdas en la zona intermedia y extremos de algunos modelos, b) Modo 2, fallas globales en las venas de las mallas de metal expandido que se denominó pandeo global y c) Modo 3, fallas locales, en el cual el material llegó a fluencia en los nodos e hizo que las venas flectaran y se cerraran entre sí. Este modo de falla se definió como aplastamiento local.

3.1 Modo de colapso en la orientación α=0º

Las Figuras 15a y 15b muestran la secuencia de deformación en los modelos de sección cuadrada y circular respectivamente durante el ensayo de compresión. En ambos modelos el mecanismo de falla se debió principalmente al aplastamiento local de las celdas desde la zona intermedia hacia los extremos de los mismos.

Con el objeto de caracterizar el comportamiento de las probetas en esta orientación, en la Figura 16 se observa en detalle la secuencia de deformación de las celdas.

Como se observa en las Figuras 16a y 16b una vez que los nodos en las celdas llegan a la fluencia, se inicia un mecanismo de colapso plástico que genera el desplazamiento progresivo de los mismos. A medida que se desarrolla el ensayo se produce una reducción considerable del porcentaje de área libre en el interior de las celdas debido al aplastamiento progresivo de las venas. (Figura16c). Luego que se ha producido el cierre completo de la celda, comienzan a originarse interacciones y contactos entre las celdas completamente cerradas las cuales generan a su vez nuevos aplastamientos de las celdas contiguas. (Figura 16d). En la Figura 17, se muestra el estado final de los modelos MA003 y MB005 para desplazamientos superiores a 225 mm. Puede verificarse que la respuesta de estos modelos sometidos a cargas de aplastamiento axial fue significativamente más controlada en comparación con el resto de los modelos estudiados.

3.2 Modelos en la orientación α=30º

En las Figuras 18a y 18b se observan respectivamente las secuencias de deformación para los modelos de sección cuadrada y circular que fueron estudiados en la orientación α=30º. Puede verificarse que ambos modelos presentaron un comportamiento muy similar. En este caso la dirección de aplastamiento de la celda (diagonal menor) no coincide con la dirección de la carga impuesta. Esto produce una inestabilidad por aplastamiento local en la celda similar a la generada en la orientación anterior la cual provoca el desequilibrio parcial del elemento y acentúa las características de falla por pandeo global.

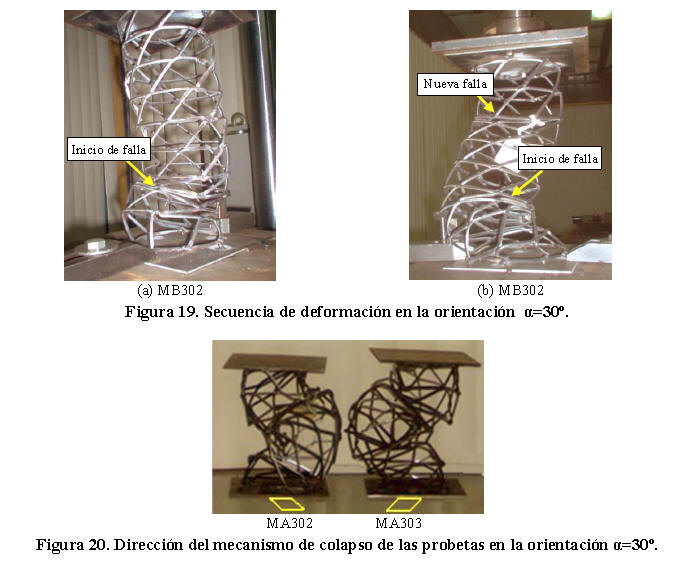
En la Figura 19 se describe la secuencia de deformación de las celdas para esta orientación. En este caso el eje geométrico forma 30º con la horizontal y las venas en dirección del eje del material forman aproximadamente 38º con la dirección de aplicación de la carga. En la Figura 19a, una vez que las venas llegan a la fluencia se produce el pandeo local de las mismas hacia la dirección del eje del material. En esta dirección las celdas encuentran menor resistencia a ser deformadas y tratan de recobrar su forma original lo cual favorece el aplastamiento local en diferentes secciones sobre la superficie de las probetas. Al producirse el contacto de las celdas y la formación consecutiva de filas de celdas adyacentes parcialmente deformadas, se genera una pérdida de estabilidad que provoca finalmente el pandeo global del elemento. (Figura 19b). Como se observará posteriormente en esta orientación y en las orientaciones α=45º y α=60º el mecanismo de colapso plástico no sólo depende de la orientación del rombo, sino también de la dirección del mismo. Es decir, según la dirección en la cual se localice el eje del material de la malla de metal expandido, en esa dirección se orientará la torsión y el mecanismo de falla de la probeta. (Figura 20). Por lo tanto puede afirmarse que en estos casos la deformación es antisimétrica comparada con la correspondencia entre los ángulos reflejados.

3.3 Modelos en la orientación α=45º

Las Figuras 21a y 21b muestran respectivamente la secuencia de deformación de los modelos de sección cuadrada y circular para esta orientación. El mecanismo de colapso en ambos modelos estuvo caracterizado por una combinación de efectos producidos por el aplastamiento irregular de las celdas en uno de los extremos de las probetas y una línea de falla definida por inestabilidades locales de las venas en la dirección del eje del material. Estos efectos en conjunto ocasionaron el colapso pandeo global de los modelos estudiados en esta orientación. En la Figura 22, se detalla el modo de falla de las celdas para esta orientación. Como se observa en esta figura, luego del aplastamiento parcial de las celdas cerca de los extremos, se produce el pandeo local de las venas en la dirección del eje del material lo que genera a su vez una línea de falla alrededor de la superficie de la probeta. Cuando se produce la plastificación de las venas sobre la línea de falla se produce una pérdida de estabilidad que provoca el colapso por pandeo global de todo el elemento. La Figuras 23 muestra que el inicio de la falla y el mecanismo de colapso de estos modelos presentó un comportamiento similar al exhibido por los modelos ensayados en la orientación α=30º cuando se modificó la dirección del rombo.

3.4 Modelos en la orientación α=60º

Las secuencias de ensayo de los modelos con sección cuadrada y circular para esta orientación se muestran en la Figura 24 y Figura 25. De forma general, en ambos modelos el modo de falla se produjo por pandeo global. El mecanismo de colapso se inició por inestabilidad local de las venas en la dirección vertical del eje del material a través de una línea de falla que se generó consistentemente alrededor de toda la superficie de las probetas. Esta línea de falla presentó un comportamiento similar al mostrado por una curva helicoidal (Figura 25d).

En la Figura 25, se ilustra un modelo simple de deformación de las celdas para esta orientación. En las Figuras 25a, 25b y 25c una vez que las venas llegan a la fluencia, las mismas pandean progresiva y localmente. Esto provoca el contacto entre ambos ejes generando un ligero aumento de la carga y al mismo tiempo una pérdida de estabilidad con grandes desplazamientos que provocan finalmente el colapso por pandeo global de todo el elemento. (Figura 25d).

Como se observa, el mecanismo de colapso plástico en estos modelos se produce inicialmente por fluencia en las venas y luego por pandeo global. De igual forma se observó que en esta orientación también se produce una deformación antisimétrica y una ligera torsión en las probetas. Estos efectos, como se ha indicado en las orientaciones previas dependen de la dirección de las celdas.

3.5 Modelos en la orientación α=90º

Las Figuras 26a y 26b muestran las secuencias de deformación de los modelos de sección cuadrada y circular respectivamente para esta orientación. En este ensayo la dirección de la carga coincide con el eje geométrico mayor (dh) de la lámina de metal expandido. Aún cuando en el estado final de colapso para ambos modelos se observaron ligeras variaciones, característicamente todas las probetas estudiadas presentaron un ensanchamiento (barreling) en la sección intermedia el cual fue originado por el pandeo en las venas de las celdas. Posteriormente debido a la plastificación gradual en los nodos, se produjo el aplastamiento local y progresivo de las celdas en la dirección del eje geométrico mayor (dh).

En la Figura 27 se muestra la deformación de las celdas para esta orientación. Una vez que se comienza a cargar el sistema, las celdas tienden a cerrarse en la dirección más larga del rombo. Este efecto, hace que gran parte de las venas en las celdas ubicadas en la sección intermedia pandeen y en consecuencia provoquen una reducción en la capacidad de carga. A medida que el sistema continúa deformándose se adiciona área efectiva de trabajo que provoca un incremento de carga debido al aumento de rigidez en los nodos de las celdas. En el caso de las probetas de sección circular (Figura 28a) se observó para un nivel de desplazamiento superior a 100 mm, la formación de un anillo circular cerca de la sección intermedia sobre el cual se produjo posteriormente el aplastamiento progresivo de las celdas contiguas. Este anillo alcanzó un diámetro aproximado de dos (02) veces el diámetro inicial de la probeta. En relación a las probetas de sección cuadrada, para un nivel de desplazamiento similar al anterior, se observó la formación de una sección irregular rígida próxima a la zona intermedia sobre la cual también se produjo el aplastamiento progresivo de las celdas adyacentes (Figura 28b).

4. CONCLUSIONES

De los resultados obtenidos en esta investigación se concluye que: El factor de eficiencia estructural revela que los modelos estudiados en la orientación α=0º presentan una respuesta más estable para aplicaciones de absorción de energía en comparación con el resto. En ambos casos el factor de eficiencia estructural fue muy cercano a uno (1). En este sentido las curvas obtenidas en estos modelos exhiben una transición suave del rango elástico al plástico con un comportamiento mucho más uniforme en comparación con el resto, lo cual evidencia las grandes ventajas de esta orientación para aplicaciones de absorción de energía. Las probetas de sección cuadrada presentan una capacidad de carga media de colapso y absorción de energía mayor entre 1% y 7% con respecto a las probetas de sección circular excepto en la orientación α=30º donde la carga media de colapso y energía absorbida por las probetas de sección circular fue 9% mayor. La carga media y absorción de energía dependen significativamente de la orientación del rombo de la malla de metal expandido. Para algunas orientaciones la capacidad de carga media de colapso y energía absorbida aumentó hasta 290%. De igual manera en este estudio se observó que el mecanismo de colapso plástico y la torsión de los modelos dependen significativamente de la dirección de los ejes del material de la malla de metal expandido con respecto a la carga aplicada. En ambas geometrías se producen esencialmente tres (03) mecanismos de colapso plástico: 1) aplastamientos irregulares e inestables de las celdas en la zona intermedia y extremos de algunos modelos; 2) fallas globales en las celdas de algunos modelos que se denominó pandeo global; 3) fallas locales de las celdas, en el cual el material llegó a fluencia en los nodos ocasionando que las venas flectaran y se cerraran entre sí.

5. AGRADECIMIENTOS

Los autores quieren agradecer a la Universidad Nacional Experimental Francisco de Miranda y al Decanato de Investigación de la Universidad Simón Bolívar por el apoyo prestado. Así mismo se agradece a la empresa de fabricación y suministro de láminas de metal expandido Maboca C.A.

6. REFERENCIAS

1. Aalberg, A. y Haugen, B. (1997). An experimental investigation of a rectangular hollow steel section with solid corners and expanded metal sections. Department of Structural Engineering. Norwegian University of Science Technology. ISBN 91-973094-0-0. Report. No. R-8-97. 77 p.         [ Links ]

2. Alghamdi, A. (2001). Collapsible impact energy absorbers: an Overview. Journal of Thin Walled Structures, 39, 189-213.

3. ASTM E9 89a (2000). Standard test methods of compression testing of metallic materials at room temperature. American Society for Testing and Materials. Michigan. DOI: 10.1520/E0009-89AR00

4. Ayestarán, A., Graciano, C. y Díaz, S. (2006). Análisis por elementos finitos de un dispositivo para la absorción de energía de impacto empleando mallas de metal expandido. Tesis de Grado, Universidad Simón Bolívar, Caracas-Venezuela.

5. Bergey, K. (2002). A new approach to the design of energy absorbing seats. American Institute of Aeronautical and Astronautics (AIAA-2002-5848). University of Oklahoma. Los Angeles- California.

6. Escalona, L. (2005). Estudio experimental de la capacidad de absorción de energía por deformación del crush zone del vehículo F-SAE USB 2005. Tesis de Grado, Universidad Simón Bolívar, Caracas-Venezuela.

7. Hellsten, M. (1998a). Technique, qualities and modeling of beams with expanded metal sections. Journal of Constructional Steel Research., 46, 486-487.

8. Hellsten, M. (1998b). Closed beam with expanded metal sections. US. Patent No. 5,778,626. July 14, 1998. Appl. 836,178. Sept. 2, 1997. 7 p.

9. Hosseinipour, S. y Daneshi, G. (2003). Energy absorption and mean load of thin-walled grooved tubes under axial compression. Journal of Thin Walled Structures, 41, 31-46.

10. Huang, X., Lu, G. y Yu, T. (2002). Energy absorption in splitting square metal tubes. Journal of Thin Walled Structures, 40, 153-165.

11. Kooistra, G. y Wadley, H. (2005). Lattice truss structures from expanded metal sheet. Materials and Design, 28, 507-514.

12. Mamalis, A., Manolakos, D. y Viegelhan, G. (1989). The axial crushing of thin PVC tubes and frusta of square cross-section. International Journal of Impact Engineering 8(3):241–64.

13. Maboca C.A. (2007). Disponible on line: http://www.maboca.com.ve. [Consulta: 2007, Octubre 4].

14. Mulder, D. (2005). Expanded metal. US. Patent No. US 2005/0060858 A1. March 24, 2005. Appl. 10/913,929. Aug. 6, 2004. 20 p.

15. Olabi, A., Morris, E. y Hashmi, M. (2007). Metallic tube type energy absorbers. Journal of Thin Walled Structures, 45, 706 -726.

16. Oliveira, J., Barros, J., Lorenzo, P. y Marques, A. (2002). Uniaxial testing of expanded metal sheet. Universidad do Minho-GROW-1999-70420 “ISO-BRICK” from the European Comission. Report 02-DEC/E-11. Portugal, Azurém. 31 p.

17. Jitaru, L. y Cristescu, G. (2007). Mathematical modelling the force-displacement dependence for expanded metal threads. University of Arad, România. Fascicle of management and technological engineering, Vol. VI, (XVI), 2007. 8 p.

18. Sánchez, R. y Graciano, C. (2005). Determinación de las propiedades mecánicas de láminas de metal expandido. Tesis de Maestría, Universidad Simón Bolívar, Caracas-Venezuela.

19. Storck, A. (1894). Concrete Block with Expanded Metal reinforce core. US. Patent No. 512,128. Jan. 2, 1894. Appl. 436,866. June 15, 1892. 4 p.

20. Tarigopula, V., Langseth, M., Hopperstad, O. y Clausen, A. (2005). Axial crushing of thin-walled high-strength steel sections. International Journal of Impact Engineering, 32, 847–882.